Codeforces 429B Working out：dp【列舉交點】

Leohh發表於2018-01-04

題目連結：http://codeforces.com/problemset/problem/429/B

題意：

　　給你一個n*m的網格，每個格子上有一個數字a[i][j]。

　　一個人從左上角走到右下角，一個人從左下角走到右上角，要求兩條路徑有且僅有一個交點。

　　問你除去交點格子上的數字，路徑上數字之和最大是多少。

 

題解：

　　表示狀態：

　　　　dp[i][j][0/1/2/3] = max sum

　　　　表示從某個角走到(i,j)這個格子，最大路徑上數字之和

　　　　0,1,2,3分別代表左上角、右上角、左下角、右下角

 

　　找出答案：

　　　　路徑相交共有兩種方式：

　　　　

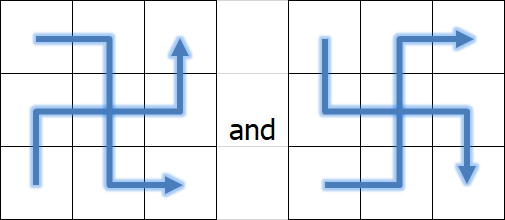
　　　　列舉交點(i,j)。

　　　　ans = max dp[i-1][j][0] + dp[i+1][j][3] + dp[i][j-1][2] + dp[i][j+1][1]

　　　　ans = max dp[i-1][j][1] + dp[i+1][j][2] + dp[i][j-1][0] + dp[i][j+1][3]

 

　　如何轉移：

　　　　四種情況分別算：

　　　　（1）dp[i][j][0] = max dp[i-1][j][0]+a[i][j]

　　　　　　 dp[i][j][0] = max dp[i][j-1][0]+a[i][j]

　　　　（2）dp[i][j][1] = max dp[i-1][j][1]+a[i][j]

　　　　　　 dp[i][j][1] = max dp[i][j+1][1]+a[i][j]

　　　　（3）dp[i][j][2] = max dp[i+1][j][2]+a[i][j]

　　　　　　 dp[i][j][2] = max dp[i][j-1][2]+a[i][j]

　　　　（4）dp[i][j][3] = max dp[i+1][j][3]+a[i][j]

　　　　　　 dp[i][j][3] = max dp[i][j+1][3]+a[i][j]

 

　　邊界條件：

　　　　set dp = 0

 

AC Code:

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #define MAX_N 1005
 5 
 6 using namespace std;
 7 
 8 int n,m;
 9 int a[MAX_N][MAX_N];
10 int dp[MAX_N][MAX_N][4];
11 
12 void read()
13 {
14     cin>>n>>m;
15     for(int i=1;i<=n;i++)
16     {
17         for(int j=1;j<=m;j++)
18         {
19             cin>>a[i][j];
20         }
21     }
22 }
23 
24 void work()
25 {
26     memset(dp,0,sizeof(dp));
27     for(int i=1;i<=n;i++)
28     {
29         for(int j=1;j<=m;j++)
30         {
31             dp[i][j][0]=max(dp[i][j][0],dp[i-1][j][0]+a[i][j]);
32             dp[i][j][0]=max(dp[i][j][0],dp[i][j-1][0]+a[i][j]);
33         }
34     }
35     for(int i=1;i<=n;i++)
36     {
37         for(int j=m;j>=1;j--)
38         {
39             dp[i][j][1]=max(dp[i][j][1],dp[i-1][j][1]+a[i][j]);
40             dp[i][j][1]=max(dp[i][j][1],dp[i][j+1][1]+a[i][j]);
41         }
42     }
43     for(int i=n;i>=1;i--)
44     {
45         for(int j=1;j<=m;j++)
46         {
47             dp[i][j][2]=max(dp[i][j][2],dp[i+1][j][2]+a[i][j]);
48             dp[i][j][2]=max(dp[i][j][2],dp[i][j-1][2]+a[i][j]);
49         }
50     }
51     for(int i=n;i>=1;i--)
52     {
53         for(int j=m;j>=1;j--)
54         {
55             dp[i][j][3]=max(dp[i][j][3],dp[i+1][j][3]+a[i][j]);
56             dp[i][j][3]=max(dp[i][j][3],dp[i][j+1][3]+a[i][j]);
57         }
58     }
59     int ans=0;
60     for(int i=2;i<n;i++)
61     {
62         for(int j=2;j<m;j++)
63         {
64             ans=max(ans,dp[i-1][j][0]+dp[i+1][j][3]+dp[i][j-1][2]+dp[i][j+1][1]);
65             ans=max(ans,dp[i-1][j][1]+dp[i+1][j][2]+dp[i][j-1][0]+dp[i][j+1][3]);
66         }
67     }
68     cout<<ans<<endl;
69 }
70 
71 int main()
72 {
73     read();
74     work();
75 }

 

相關文章