RQNOJ 514 字串距離：dp & 字串

Leohh發表於2017-09-01
字串

題目連結：https://www.rqnoj.cn/problem/514

題意：

　　設有字串X，我們稱在X的頭尾及中間插入任意多個空格後構成的新字串為X的擴充套件串，如字串X為”abcbcd”，則字串”abcb_cd”，”_a_bcbcd_”和”abcb_cd_”都是X的擴充套件串，這裡“_”代表空格字元。

　　如果A1是字串A的擴充套件串，B1是字串B的擴充套件串，A1與B1具有相同的長度，那麼我捫定義字串A1與B1的距離為相應位置上的字元的距離總和，而兩個非空格字元的距離定義為它們的ASCII碼的差的絕對值，而空格字元與其他任意字元之間的距離為已知的定值K，空格字元與空格字元的距離為0。在字串A、B的所有擴充套件串中，必定存在兩個等長的擴充套件串A1、B1，使得A1與B1之間的距離達到最小，我們將這一距離定義為字串A、B的距離。

　　請你寫一個程式，求出字串A、B的距離。

 

題解：

　　先舉個例子：

　　A = "ABC", B = "DEFG"

　　

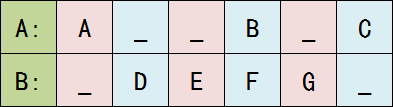
　　這是其中的一種匹配情況。

　　而每一種匹配，無非是由一些上下字元對組合而成。

　　比如例子的組成：(A,_) , (_,D) , (_,E) , (B,F) , (_,G) , (C,_)

　　有兩個很顯然的結論：

　　　　（1）一種匹配不可能有一組為(_,_)，因為它對答案不能做出任何貢獻。

　　　　（2）字元組的排列有順序，不可能存在左邊為(A,E)，右邊為(B,D)。

 

　　那麼可以轉化問題：

　　　　求一個這樣的匹配，上面只有A串字元，下面只有B串字元，同時使得匹配中的每一個字母與兩個原串中的字母一一對應。

 

　　類似揹包吧。。。

 

　　表示狀態：

　　　　dp[i][j] = min distance

　　　　i：A串考慮到第i個字元

　　　　j：B串考慮到第j個字元

 

　　找出答案：

　　　　ans = dp[a.len][b.len]

 

　　如何轉移：

　　　　now: dp[i][j]

　　　　三種決策，往匹配中新增字元對：

　　　　　　（1）(a[i],_)

　　　　　　（2）(_,b[j])

　　　　　　（3）(a[i],b[j])

　　　　分別對應方程：

　　　　　　dp[i+1][j] = min dp[i][j] + space

　　　　　　dp[i][j+1] = min dp[i][j] + space

　　　　　　dp[i+1][j+1] = min dp[i][j] + abs(a[i]-b[j])

 

　　邊界條件:

　　　　dp[0][0] = 0

　　　　others = -1

　　　　什麼都還沒有新增。。。

 

AC Code:

 1 // state expression:
 2 // dp[i][j] = min distance
 3 // i: considering ith char in str a
 4 // j: considering ith char in str b
 5 //
 6 // find the answer:
 7 // ans = dp[a.len][b.len]
 8 //
 9 // transferring:
10 // now: dp[i][j]
11 // dp[i+1][j] = min dp[i][j] + space
12 // dp[i][j+1] = min dp[i][j] + space
13 // dp[i+1][j+1] = min dp[i][j] + abs(a[i]-b[j])
14 //
15 // boundary:
16 // dp[0][0] = 0
17 // others = -1
18 #include <iostream>
19 #include <stdio.h>
20 #include <string.h>
21 #include <stdlib.h>
22 #define MAX_L 2005
23 
24 using namespace std;
25 
26 int space;
27 int dp[MAX_L][MAX_L];
28 string a,b;
29 
30 void read()
31 {
32     cin>>a>>b>>space;
33 }
34 
35 int my_min(int a,int b)
36 {
37     if(a==-1) return b;
38     if(b==-1) return a;
39     return min(a,b);
40 }
41 
42 void solve()
43 {
44     memset(dp,-1,sizeof(dp));
45     dp[0][0]=0;
46     for(int i=0;i<=a.size();i++)
47     {
48         for(int j=0;j<=b.size();j++)
49         {
50             if(dp[i][j]!=-1)
51             {
52                 dp[i+1][j]=my_min(dp[i+1][j],dp[i][j]+space);
53                 dp[i][j+1]=my_min(dp[i][j+1],dp[i][j]+space);
54                 dp[i+1][j+1]=my_min(dp[i+1][j+1],dp[i][j]+abs(a[i]-b[j]));
55             }
56         }
57     }
58 }
59 
60 void print()
61 {
62     cout<<dp[a.size()][b.size()]<<endl;
63 }
64 
65 int main()
66 {
67     read();
68     solve();
69     print();
70 }

 

相關文章