計蒜客模擬賽D2T1 蒜頭君的兔子：矩陣快速冪

Leohh發表於2017-07-31
矩陣

題目連結：https://nanti.jisuanke.com/t/16442

題意：

　　有個人在第一年送了你一對1歲的兔子。這種兔子剛生下來的時候算0歲，當它在2~10歲的時候，每年都會生下一對兔子，並且它在10歲那年生完兔子後就會掛掉。現在讓你算出第t年兔子的總數（不算那一年10歲的兔子）。

 

題解：

　　我們用一個1*10的矩陣代表某一年的兔子數量，第k列上的數字n代表今年有n只k歲的兔子。

　　那麼初始矩陣是這樣的：

　　

　　接下來考慮怎樣構造特殊矩陣。

　　有兩個轉移關係：

　　　　第二年0歲的兔子數 = 第二年2~10歲的兔子數之和 = 今年1~9歲的兔子數之和

　　　　第二年k (1<=k<=10) 歲的兔子數 = 今年k-1歲的兔子數

　　也就是這樣轉移：

　　

　　b[0] = a[1] + a[2] + ... + a[9]

　　b[1] = a[0]

　　b[2] = a[1]

　　...

　　b[9] = a[8]

　　b[10] = a[9]

　　那麼特殊矩陣也就出來了：

　　

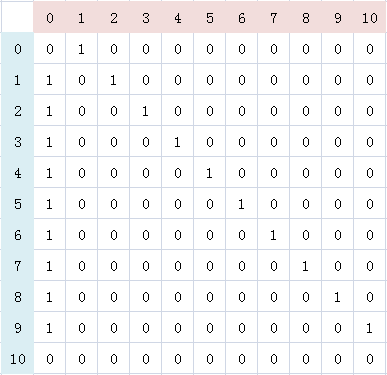
　　所以第t年的矩陣ans = 初始矩陣start * ( 特殊矩陣special ^ (t-1) )

　　優化：由於在整個過程中根本沒有用到每年10歲的兔子數量，所以可以省去初始矩陣的第10列，以及特殊矩陣的第10列&第10行。

 

AC Code：

#include <iostream>
#include <stdio.h>
#include <string.h>
#define MAX_L 15
#define MOD 1000000007

using namespace std;

struct Mat
{
    int n;
    int m;
    long long v[MAX_L][MAX_L];
    Mat()
    {
        memset(v,0,sizeof(v));
        n=0;
        m=0;
    }
};

int t;
long long sum=0;

Mat make_unit(int k)
{
    Mat mat;
    mat.n=k;
    mat.m=k;
    for(int i=0;i<k;i++)
    {
        mat.v[i][i]=1;
    }
    return mat;
}

Mat make_start()
{
    Mat mat;
    mat.n=1;
    mat.m=10;
    mat.v[0][1]=1;
    return mat;
}

Mat make_special()
{
    Mat mat;
    mat.n=10;
    mat.m=10;
    for(int i=1;i<=9;i++)
    {
        mat.v[i][0]=1;
        mat.v[i-1][i]=1;
    }
    return mat;
}

Mat mul_mat(const Mat &a,const Mat &b)
{
    Mat c;
    c.n=a.n;
    c.m=b.m;
    for(int i=0;i<a.n;i++)
    {
        for(int j=0;j<b.m;j++)
        {
            for(int k=0;k<a.m;k++)
            {
                c.v[i][j]+=(a.v[i][k]*b.v[k][j])%MOD;
                c.v[i][j]%=MOD;
            }
        }
    }
    return c;
}

Mat quick_pow_mat(Mat mat,long long k)
{
    Mat ans;
    ans=make_unit(mat.n);
    while(k)
    {
        if(k&1)
        {
            ans=mul_mat(ans,mat);
        }
        k>>=1;
        mat=mul_mat(mat,mat);
    }
    return ans;
}

void read()
{
    cin>>t;
}

void solve()
{
    Mat start=make_start();
    Mat special=make_special();
    Mat ans=mul_mat(start,quick_pow_mat(special,t-1));
    for(int i=0;i<=9;i++)
    {
        sum=(sum+ans.v[0][i])%MOD;
    }
}

void print()
{
    cout<<sum<<endl;
}

int main()
{
    read();
    solve();
    print();
}

 

相關文章