在文字主題模型之潛在語義索引(LSI)中,我們講到LSI主題模型使用了奇異值分解,面臨著高維度計算量太大的問題。這裡我們就介紹另一種基於矩陣分解的主題模型:非負矩陣分解(NMF),它同樣使用了矩陣分解,但是計算量和處理速度則比LSI快,它是怎麼做到的呢?
1. 非負矩陣分解(NMF)概述
非負矩陣分解(non-negative matrix factorization,以下簡稱NMF)是一種非常常用的矩陣分解方法,它可以適用於很多領域,比如影象特徵識別,語音識別等,這裡我們會主要關注於它在文字主題模型裡的運用。
回顧奇異值分解,它會將一個矩陣分解為三個矩陣:$$A = U\Sigma V^T$$
如果降維到$k$維,則表示式為:$$A_{m \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n}$$
但是NMF雖然也是矩陣分解,它卻使用了不同的思路,它的目標是期望將矩陣分解為兩個矩陣:$$A_{m \times n} \approx W_{m \times k}H_{k \times n}$$
分解成兩個矩陣是不是一定就比SVD省時呢?這裡的理論不深究,但是NMF的確比SVD快。不過如果大家讀過我寫的矩陣分解在協同過濾推薦演算法中的應用,就會發現裡面的FunkSVD所用的演算法思路和NMF基本是一致的,只不過FunkSVD聚焦於推薦演算法而已。
那麼如何可以找到這樣的矩陣呢?這就涉及到NMF的優化思路了。
2. NMF的優化思路
NMF期望找到這樣的兩個矩陣$W,H$,使$WH$的矩陣乘積得到的矩陣對應的每個位置的值和原矩陣$A$對應位置的值相比誤差儘可能的小。用數學的語言表示就是:$$\underbrace{arg\;min}_{W,H}\frac{1}{2}\sum\limits_{i,j}(A_{ij}-(WH)_{ij})^2$$
如果完全用矩陣表示,則為:$$\underbrace{arg\;min}_{W,H}\frac{1}{2}||A-WH||_{Fro}^2$$
其中,$ ||*||_{Fro}$為Frobenius範數。
當然對於這個式子,我們也可以加上L1和L2的正則化項如下:
$$\underbrace{arg\;min}_{W,H}\frac{1}{2}||A-WH||_{Fro}^2 +\alpha\rho|| W||_1+\alpha\rho|| H||_1+\frac{\alpha(1-\rho)}{2}|| W||_{Fro}^2 + \frac{\alpha(1-\rho)}{2}|| H||_{Fro}^2$$
其中,$\alpha$為L1&L2正則化引數,而$\rho$為L1正則化佔總正則化項的比例。$||*||_1$為L1範數。
我們要求解的有$m*k + k*n$個引數。引數不少,常用的迭代方法有梯度下降法和擬牛頓法。不過如果我們決定加上了L1正則化的話就不能用梯度下降和擬牛頓法了。此時可以用座標軸下降法或者最小角迴歸法來求解。scikit-learn中NMF的庫目前是使用座標軸下降法來求解的,,即在迭代時,一次固定$m*k + k*n-1$個引數,僅僅最優化一個引數。這裡對優化求$W,H$的過程就不再寫了,如果大家對座標軸下降法不熟悉,參看之前寫的這一篇Lasso迴歸演算法: 座標軸下降法與最小角迴歸法小結。
3. NMF 用於文字主題模型
回到我們本文的主題,NMF矩陣分解如何運用到我們的主題模型呢?
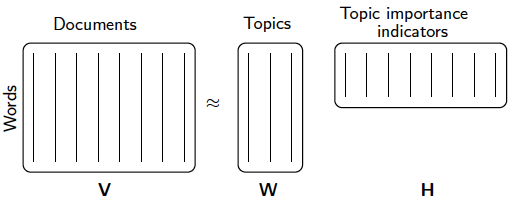
此時NMF可以這樣解釋:我們輸入的有m個文字,n個詞,而$A_{ij}$對應第i個文字的第j個詞的特徵值,這裡最常用的是基於預處理後的標準化TF-IDF值。k是我們假設的主題數,一般要比文字數少。NMF分解後,$W_{ik}$對應第i個文字的和第k個主題的概率相關度,而$H_{kj}$對應第j個詞和第k個主題的概率相關度。
當然也可以反過來去解釋:我們輸入的有m個詞,n個文字,而$A_{ij}$對應第i個詞的第j個文字的特徵值,這裡最常用的是基於預處理後的標準化TF-IDF值。k是我們假設的主題數,一般要比文字數少。NMF分解後,$W_{ik}$對應第i個詞的和第k個主題的概率相關度,而$H_{kj}$對應第j個文字和第k個主題的概率相關度。
注意到這裡我們使用的是"概率相關度",這是因為我們使用的是"非負"的矩陣分解,這樣我們的$W,H$矩陣值的大小可以用概率值的角度去看。從而可以得到文字和主題的概率分佈關係。第二種解釋用一個圖來表示如下:
和LSI相比,我們不光得到了文字和主題的關係,還得到了直觀的概率解釋,同時分解速度也不錯。當然NMF由於是兩個矩陣,相比LSI的三矩陣,NMF不能解決詞和詞義的相關度問題。這是一個小小的代價。
4. scikit-learn NMF的使用
在 scikit-learn中,NMF在sklearn.decomposition.NMF包中,它支援L1和L2的正則化,而$W,H$的求解使用座標軸下降法來實現。
NMF需要注意的引數有:
1) n_components:即我們的主題數k, 選擇k值需要一些對於要分析文字主題大概的先驗知識。可以多選擇幾組k的值進行NMF,然後對結果人為的進行一些驗證。
2) init : 用於幫我們選擇$W,H$迭代初值的演算法, 預設是None,即自動選擇值,不使用選擇初值的演算法。如果我們對收斂速度不滿意,才需要關注這個值,從scikit-learn提供的演算法中選擇一個合適的初值選取演算法。
3)alpha: 即我們第三節中的正則化引數$\alpha$,需要調參。開始建議選擇一個比較小的值,如果發現效果不好在調參增大。
4) l1_ratio: 即我們第三節中的正則化引數$\rho$,L1正則化的比例,僅在$\alpha>0$時有效,需要調參。開始建議不使用,即用預設值0, 如果對L2的正則化不滿意再加上L1正則化。
從上面可見,使用NMF的關鍵引數在於主題數的選擇n_components和正則化的兩個超引數$\alpha,\rho$。
此外,$W$矩陣一般在呼叫fit_transform方法的返回值裡獲得,而$H$矩陣則儲存在NMF類的components_成員中。
下面我們給一個例子,我們有4個詞,5個文字組成的矩陣,需要找出這些文字和隱含的兩個主題之間的關係。程式碼如下:
完整程式碼參見我的github:https://github.com/ljpzzz/machinelearning/blob/master/natural-language-processing/nmf.ipynb
import numpy as np X = np.array([[1,1,5,2,3], [0,6,2,1,1], [3, 4,0,3,1], [4, 1,5,6,3]]) from sklearn.decomposition import NMF model = NMF(n_components=2, alpha=0.01)
現在我們看看分解得到的$W,H$:
W = model.fit_transform(X) H = model.components_ print W print H
結果如下:
[[ 1.67371185 0.02013017] [ 0.40564826 2.17004352] [ 0.77627836 1.5179425 ] [ 2.66991709 0.00940262]] [[ 1.32014421 0.40901559 2.10322743 1.99087019 1.29852389] [ 0.25859086 2.59911791 0.00488947 0.37089193 0.14622829]]
從結果可以看出, 第1,3,4,5個文字和第一個隱含主題更相關,而第二個文字與第二個隱含主題更加相關。如果需要下一個結論,我們可以說,第1,3,4,5個文字屬於第一個隱含主題,而第二個問題屬於第2個隱含主題。
5. NMF的其他應用
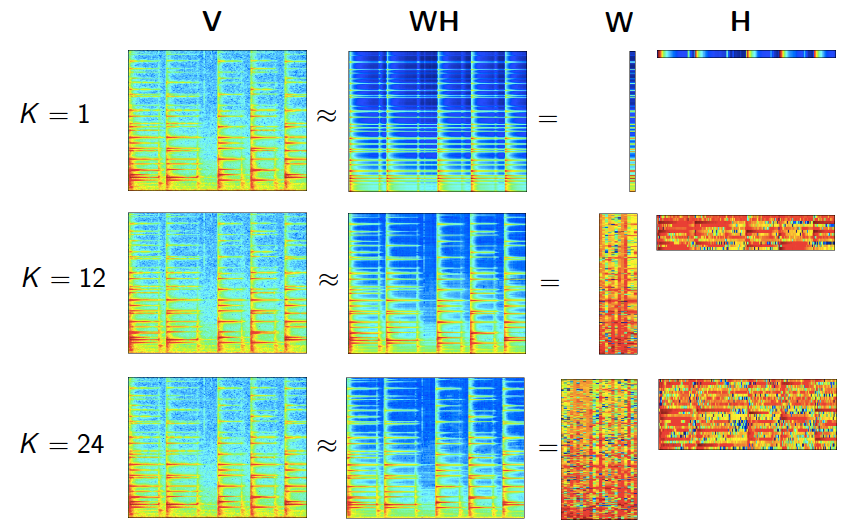
雖然我們是在主題模型裡介紹的NMF,但實際上NMF的適用領域很廣,除了我們上面說的影象處理,語音處理,還包括訊號處理與醫藥工程等,是一個普適的方法。在這些領域使用NMF的關鍵在於將NMF套入一個合適的模型,使得$W,H$矩陣都可以有明確的意義。這裡給一個圖展示NMF在做語音處理時的情形:
6. NMF主題模型小結
NMF作為一個漂亮的矩陣分解方法,它可以很好的用於主題模型,並且使主題的結果有基於概率分佈的解釋性。但是NMF以及它的變種pLSA雖然可以從概率的角度解釋了主題模型,卻都只能對訓練樣本中的文字進行主題識別,而對不在樣本中的文字是無法識別其主題的。根本原因在於NMF與pLSA這類主題模型方法沒有考慮主題概率分佈的先驗知識,比如文字中出現體育主題的概率肯定比哲學主題的概率要高,這點來源於我們的先驗知識,但是無法告訴NMF主題模型。而LDA主題模型則考慮到了這一問題,目前來說,絕大多數的文字主題模型都是使用LDA以及其變體。下一篇我們就來討論LDA主題模型。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)