奇異值分解(Singular Value Decomposition,以下簡稱SVD)是在機器學習領域廣泛應用的演算法,它不光可以用於降維演算法中的特徵分解,還可以用於推薦系統,以及自然語言處理等領域。是很多機器學習演算法的基石。本文就對SVD的原理做一個總結,並討論在在PCA降維演算法中是如何運用運用SVD的。
1. 回顧特徵值和特徵向量
我們首先回顧下特徵值和特徵向量的定義如下:$$Ax=\lambda x$$
其中A是一個$n \times n$的矩陣,$x$是一個$n$維向量,則我們說$\lambda$是矩陣A的一個特徵值,而$x$是矩陣A的特徵值$\lambda$所對應的特徵向量。
求出特徵值和特徵向量有什麼好處呢? 就是我們可以將矩陣A特徵分解。如果我們求出了矩陣A的$n$個特徵值$\lambda_1 \leq \lambda_2 \leq ... \leq \lambda_n$,以及這$n$個特徵值所對應的特徵向量$\{w_1,w_2,...w_n\}$,,如果這$n$個特徵向量線性無關,那麼矩陣A就可以用下式的特徵分解表示:$$A=W\Sigma W^{-1}$$
其中W是這$n$個特徵向量所張成的$n \times n$維矩陣,而$\Sigma$為這n個特徵值為主對角線的$n \times n$維矩陣。
一般我們會把W的這$n$個特徵向量標準化,即滿足$||w_i||_2 =1$, 或者說$w_i^Tw_i =1$,此時W的$n$個特徵向量為標準正交基,滿足$W^TW=I$,即$W^T=W^{-1}$, 也就是說W為酉矩陣。
這樣我們的特徵分解表示式可以寫成$$A=W\Sigma W^T$$
注意到要進行特徵分解,矩陣A必須為方陣。那麼如果A不是方陣,即行和列不相同時,我們還可以對矩陣進行分解嗎?答案是可以,此時我們的SVD登場了。
2. SVD的定義
SVD也是對矩陣進行分解,但是和特徵分解不同,SVD並不要求要分解的矩陣為方陣。假設我們的矩陣A是一個$m \times n$的矩陣,那麼我們定義矩陣A的SVD為:$$A = U\Sigma V^T$$
其中U是一個$m \times m$的矩陣,$\Sigma$是一個$m \times n$的矩陣,除了主對角線上的元素以外全為0,主對角線上的每個元素都稱為奇異值,V是一個$n \times n$的矩陣。U和V都是酉矩陣,即滿足$U^TU=I, V^TV=I$。下圖可以很形象的看出上面SVD的定義:
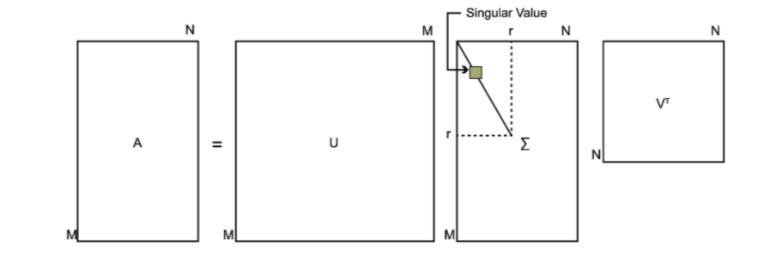
那麼我們如何求出SVD分解後的$U, \Sigma, V$這三個矩陣呢?
如果我們將A的轉置和A做矩陣乘法,那麼會得到$n \times n$的一個方陣$A^TA$。既然$A^TA$是方陣,那麼我們就可以進行特徵分解,得到的特徵值和特徵向量滿足下式:$$(A^TA)v_i = \lambda_i v_i$$
這樣我們就可以得到矩陣$A^TA$的n個特徵值和對應的n個特徵向量$v$了。將$A^TA$的所有特徵向量張成一個$n \times n$的矩陣V,就是我們SVD公式裡面的V矩陣了。一般我們將V中的每個特徵向量叫做A的右奇異向量。
如果我們將A和A的轉置做矩陣乘法,那麼會得到$m \times m$的一個方陣$AA^T$。既然$AA^T$是方陣,那麼我們就可以進行特徵分解,得到的特徵值和特徵向量滿足下式:$$(AA^T)u_i = \lambda_i u_i$$
這樣我們就可以得到矩陣$AA^T$的m個特徵值和對應的m個特徵向量$u$了。將$AA^T$的所有特徵向量張成一個$m \times m$的矩陣U,就是我們SVD公式裡面的U矩陣了。一般我們將U中的每個特徵向量叫做A的左奇異向量。
U和V我們都求出來了,現在就剩下奇異值矩陣$\Sigma$沒有求出了。由於$\Sigma$除了對角線上是奇異值其他位置都是0,那我們只需要求出每個奇異值$\sigma$就可以了。
我們注意到:$$A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = Av_i / u_i $$
這樣我們可以求出我們的每個奇異值,進而求出奇異值矩陣$\Sigma$。
上面還有一個問題沒有講,就是我們說$A^TA$的特徵向量組成的就是我們SVD中的V矩陣,而$AA^T$的特徵向量組成的就是我們SVD中的U矩陣,這有什麼根據嗎?這個其實很容易證明,我們以V矩陣的證明為例。$$A=U\Sigma V^T \Rightarrow A^T=V\Sigma^T U^T \Rightarrow A^TA = V\Sigma^T U^TU\Sigma V^T = V\Sigma^2V^T$$
上式證明使用了:$U^TU=I, \Sigma^T\Sigma=\Sigma^2。$可以看出$A^TA$的特徵向量組成的的確就是我們SVD中的V矩陣。類似的方法可以得到$AA^T$的特徵向量組成的就是我們SVD中的U矩陣。
進一步我們還可以看出我們的特徵值矩陣等於奇異值矩陣的平方,也就是說特徵值和奇異值滿足如下關係:$$\sigma_i = \sqrt{\lambda_i}$$
這樣也就是說,我們可以不用$ \sigma_i = Av_i / u_i$來計算奇異值,也可以通過求出$A^TA$的特徵值取平方根來求奇異值。
3. SVD計算舉例
這裡我們用一個簡單的例子來說明矩陣是如何進行奇異值分解的。我們的矩陣A定義為:
$$\mathbf{A} =
\left( \begin{array}{ccc}
0& 1\\ 1& 1\\
1& 0 \end{array} \right)$$
我們首先求出$A^TA$和$AA^T$
$$\mathbf{A^TA} =
\left( \begin{array}{ccc}
0& 1 &1\\
1&1& 0 \end{array} \right) \left( \begin{array}{ccc}
0& 1\\ 1& 1\\
1& 0 \end{array} \right) = \left( \begin{array}{ccc}
2& 1 \\
1& 2 \end{array} \right)$$
$$\mathbf{AA^T} =
\left( \begin{array}{ccc}
0& 1\\ 1& 1\\
1& 0 \end{array} \right) \left( \begin{array}{ccc}
0& 1 &1\\
1&1& 0 \end{array} \right) = \left( \begin{array}{ccc}
1& 1 & 0\\ 1& 2 & 1\\
0& 1& 1 \end{array} \right)$$
進而求出$A^TA$的特徵值和特徵向量:$$\lambda_1= 3; v_1 = \left( \begin{array}{ccc}
1/\sqrt{2} \\
1/\sqrt{2} \end{array} \right); \lambda_2= 1; v_2 = \left( \begin{array}{ccc}
-1/\sqrt{2} \\
1/\sqrt{2} \end{array} \right) $$
接著求$AA^T$的特徵值和特徵向量:
$$\lambda_1= 3; u_1 = \left( \begin{array}{ccc}
1/\sqrt{6} \\ 2/\sqrt{6} \\
1/\sqrt{6} \end{array} \right); \lambda_2= 1; u_2 = \left( \begin{array}{ccc}
1/\sqrt{2} \\ 0 \\
-1/\sqrt{2} \end{array} \right); \lambda_3= 0; u_3 = \left( \begin{array}{ccc}
1/\sqrt{3} \\ -1/\sqrt{3} \\
1/\sqrt{3} \end{array} \right)$$
利用$Av_i = \sigma_i u_i, i=1,2$求奇異值:
$$
\left( \begin{array}{ccc}
0& 1\\ 1& 1\\
1& 0 \end{array} \right) \left( \begin{array}{ccc}
1/\sqrt{2} \\
1/\sqrt{2} \end{array} \right) = \sigma_1 \left( \begin{array}{ccc}
1/\sqrt{6} \\ 2/\sqrt{6} \\
1/\sqrt{6} \end{array} \right) \Rightarrow \sigma_1=\sqrt{3}$$
$$
\left( \begin{array}{ccc}
0& 1\\ 1& 1\\
1& 0 \end{array} \right) \left( \begin{array}{ccc}
-1/\sqrt{2} \\
1/\sqrt{2} \end{array} \right) = \sigma_2 \left( \begin{array}{ccc}
1/\sqrt{2} \\ 0 \\
-1/\sqrt{2} \end{array} \right) \Rightarrow \sigma_2=1$$
當然,我們也可以用$\sigma_i = \sqrt{\lambda_i}$直接求出奇異值為$\sqrt{3}$和1.
最終得到A的奇異值分解為:$$A=U\Sigma V^T = \left( \begin{array}{ccc}
1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3} \\ 2/\sqrt{6} & 0 & -1/\sqrt{3}\\
1/\sqrt{6} & -1/\sqrt{2} & 1/\sqrt{3} \end{array} \right) \left( \begin{array}{ccc}
\sqrt{3} & 0 \\ 0 & 1\\
0 & 0 \end{array} \right) \left( \begin{array}{ccc}
1/\sqrt{2} & 1/\sqrt{2} \\
-1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)$$
4. SVD的一些性質
上面幾節我們對SVD的定義和計算做了詳細的描述,似乎看不出我們費這麼大的力氣做SVD有什麼好處。那麼SVD有什麼重要的性質值得我們注意呢?
對於奇異值,它跟我們特徵分解中的特徵值類似,在奇異值矩陣中也是按照從大到小排列,而且奇異值的減少特別的快,在很多情況下,前10%甚至1%的奇異值的和就佔了全部的奇異值之和的99%以上的比例。也就是說,我們也可以用最大的k個的奇異值和對應的左右奇異向量來近似描述矩陣。也就是說:$$A_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n}$$
其中k要比n小很多,也就是一個大的矩陣A可以用三個小的矩陣$U_{m \times k},\Sigma_{k \times k} ,V^T_{k \times n}$來表示。如下圖所示,現在我們的矩陣A只需要灰色的部分的三個小矩陣就可以近似描述了。
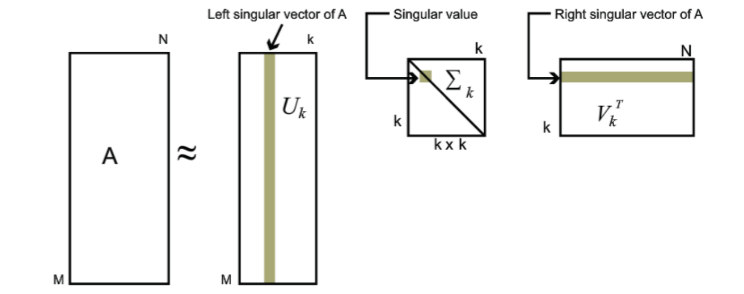
由於這個重要的性質,SVD可以用於PCA降維,來做資料壓縮和去噪。也可以用於推薦演算法,將使用者和喜好對應的矩陣做特徵分解,進而得到隱含的使用者需求來做推薦。同時也可以用於NLP中的演算法,比如潛在語義索引(LSI)。下面我們就對SVD用於PCA降維做一個介紹。
5. SVD用於PCA
在主成分分析(PCA)原理總結中,我們講到要用PCA降維,需要找到樣本協方差矩陣$X^TX$的最大的d個特徵向量,然後用這最大的d個特徵向量張成的矩陣來做低維投影降維。可以看出,在這個過程中需要先求出協方差矩陣$X^TX$,當樣本數多樣本特徵數也多的時候,這個計算量是很大的。
注意到我們的SVD也可以得到協方差矩陣$X^TX$最大的d個特徵向量張成的矩陣,但是SVD有個好處,有一些SVD的實現演算法可以不求先求出協方差矩陣$X^TX$,也能求出我們的右奇異矩陣$V$。也就是說,我們的PCA演算法可以不用做特徵分解,而是做SVD來完成。這個方法在樣本量很大的時候很有效。實際上,scikit-learn的PCA演算法的背後真正的實現就是用的SVD,而不是我們我們認為的暴力特徵分解。
另一方面,注意到PCA僅僅使用了我們SVD的右奇異矩陣,沒有使用左奇異矩陣,那麼左奇異矩陣有什麼用呢?
假設我們的樣本是$m \times n$的矩陣X,如果我們通過SVD找到了矩陣$XX^T$最大的d個特徵向量張成的$m \times d$維矩陣U,則我們如果進行如下處理:$$X'_{d \times n} = U_{d \times m}^TX_{m \times n}$$
可以得到一個$d \times n$的矩陣X‘,這個矩陣和我們原來的$m \times n$維樣本矩陣X相比,行數從m減到了d,可見對行數進行了壓縮。也就是說,左奇異矩陣可以用於行數的壓縮。相對的,右奇異矩陣可以用於列數即特徵維度的壓縮,也就是我們的PCA降維。
6. SVD小結
SVD作為一個很基本的演算法,在很多機器學習演算法中都有它的身影,特別是在現在的大資料時代,由於SVD可以實現並行化,因此更是大展身手。SVD的原理不難,只要有基本的線性代數知識就可以理解,實現也很簡單因此值得仔細的研究。當然,SVD的缺點是分解出的矩陣解釋性往往不強,有點黑盒子的味道,不過這不影響它的使用。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)