Apriori演算法是常用的用於挖掘出資料關聯規則的演算法,它用來找出資料值中頻繁出現的資料集合,找出這些集合的模式有助於我們做一些決策。比如在常見的超市購物資料集,或者電商的網購資料集中,如果我們找到了頻繁出現的資料集,那麼對於超市,我們可以優化產品的位置擺放,對於電商,我們可以優化商品所在的倉庫位置,達到節約成本,增加經濟效益的目的。下面我們就對Apriori演算法做一個總結。
1. 頻繁項集的評估標準
什麼樣的資料才是頻繁項集呢?也許你會說,這還不簡單,肉眼一掃,一起出現次數多的資料集就是頻繁項集嗎!的確,這也沒有說錯,但是有兩個問題,第一是當資料量非常大的時候,我們沒法直接肉眼發現頻繁項集,這催生了關聯規則挖掘的演算法,比如Apriori, PrefixSpan, CBA。第二是我們缺乏一個頻繁項集的標準。比如10條記錄,裡面A和B同時出現了三次,那麼我們能不能說A和B一起構成頻繁項集呢?因此我們需要一個評估頻繁項集的標準。
常用的頻繁項集的評估標準有支援度,置信度和提升度三個。
支援度就是幾個關聯的資料在資料集中出現的次數佔總資料集的比重。或者說幾個資料關聯出現的概率。如果我們有兩個想分析關聯性的資料X和Y,則對應的支援度為:$$Support(X,Y) = P(XY) = \frac{number(XY)}{num(All Samples)}$$
以此類推,如果我們有三個想分析關聯性的資料X,Y和Z,則對應的支援度為:$$Support(X,Y,Z) = P(XYZ) = \frac{number(XYZ)}{num(All Samples)}$$
一般來說,支援度高的資料不一定構成頻繁項集,但是支援度太低的資料肯定不構成頻繁項集。
置信度體現了一個資料出現後,另一個資料出現的概率,或者說資料的條件概率。如果我們有兩個想分析關聯性的資料X和Y,X對Y的置信度為$$Confidence(X \Leftarrow Y) = P(X|Y)=P(XY)/P(Y)$$
也可以以此類推到多個資料的關聯置信度,比如對於三個資料X,Y,Z,則X對於Y和Z的置信度為:$$Confidence(X \Leftarrow YZ) = P(X|YZ)=P(XYZ)/P(YZ)$$
舉個例子,在購物資料中,紙巾對應雞爪的置信度為40%,支援度為1%。則意味著在購物資料中,總共有1%的使用者既買雞爪又買紙巾;同時買雞爪的使用者中有40%的使用者購買紙巾。
提升度表示含有Y的條件下,同時含有X的概率,與X總體發生的概率之比,即:$$Lift(X \Leftarrow Y) = P(X|Y)/P(X) = Confidence(X \Leftarrow Y) / P(X)$$
提升度體先了X和Y之間的關聯關係, 提升度大於1則$X \Leftarrow Y$是有效的強關聯規則, 提升度小於等於1則$X \Leftarrow Y$是無效的強關聯規則 。一個特殊的情況,如果X和Y獨立,則有$Lift(X \Leftarrow Y) = 1$,因為此時$P(X|Y) = P(X)$。
一般來說,要選擇一個資料集合中的頻繁資料集,則需要自定義評估標準。最常用的評估標準是用自定義的支援度,或者是自定義支援度和置信度的一個組合。
2. Apriori演算法思想
對於Apriori演算法,我們使用支援度來作為我們判斷頻繁項集的標準。Apriori演算法的目標是找到最大的K項頻繁集。這裡有兩層意思,首先,我們要找到符合支援度標準的頻繁集。但是這樣的頻繁集可能有很多。第二層意思就是我們要找到最大個數的頻繁集。比如我們找到符合支援度的頻繁集AB和ABE,那麼我們會拋棄AB,只保留ABE,因為AB是2項頻繁集,而ABE是3項頻繁集。那麼具體的,Apriori演算法是如何做到挖掘K項頻繁集的呢?
Apriori演算法採用了迭代的方法,先搜尋出候選1項集及對應的支援度,剪枝去掉低於支援度的1項集,得到頻繁1項集。然後對剩下的頻繁1項集進行連線,得到候選的頻繁2項集,篩選去掉低於支援度的候選頻繁2項集,得到真正的頻繁二項集,以此類推,迭代下去,直到無法找到頻繁k+1項集為止,對應的頻繁k項集的集合即為演算法的輸出結果。
可見這個演算法還是很簡潔的,第i次的迭代過程包括掃描計算候選頻繁i項集的支援度,剪枝得到真正頻繁i項集和連線生成候選頻繁i+1項集三步。
我們下面這個簡單的例子看看:
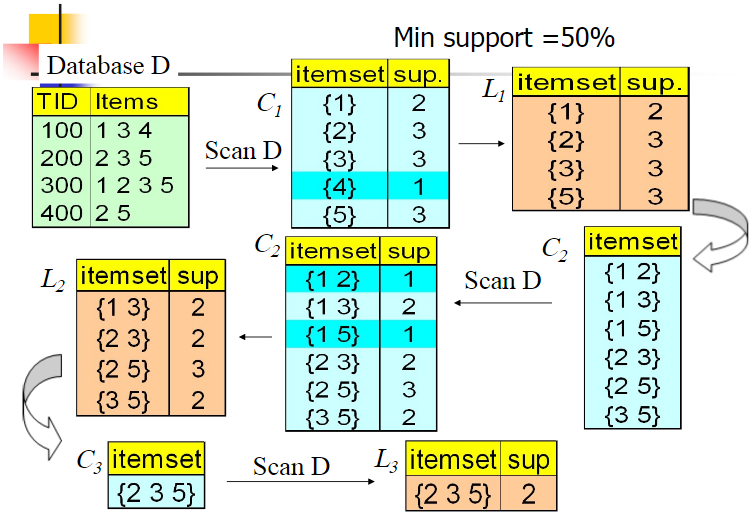
我們的資料集D有4條記錄,分別是134,235,1235和25。現在我們用Apriori演算法來尋找頻繁k項集,最小支援度設定為50%。首先我們生成候選頻繁1項集,包括我們所有的5個資料並計算5個資料的支援度,計算完畢後我們進行剪枝,資料4由於支援度只有25%被剪掉。我們最終的頻繁1項集為1235,現在我們連結生成候選頻繁2項集,包括12,13,15,23,25,35共6組。此時我們的第一輪迭代結束。
進入第二輪迭代,我們掃描資料集計算候選頻繁2項集的支援度,接著進行剪枝,由於12和15的支援度只有25%而被篩除,得到真正的頻繁2項集,包括13,23,25,35。現在我們連結生成候選頻繁3項集,123, 125,135和235共4組,這部分圖中沒有畫出。通過計算候選頻繁3項集的支援度,我們發現123,125和135的支援度均為25%,因此接著被剪枝,最終得到的真正頻繁3項集為235一組。由於此時我們無法再進行資料連線,進而得到候選頻繁4項集,最終的結果即為頻繁3三項集235。
3. Aprior演算法流程
下面我們對Aprior演算法流程做一個總結。
輸入:資料集合D,支援度閾值$\alpha$
輸出:最大的頻繁k項集
1)掃描整個資料集,得到所有出現過的資料,作為候選頻繁1項集。k=1,頻繁0項集為空集。
2)挖掘頻繁k項集
a) 掃描資料計算候選頻繁k項集的支援度
b) 去除候選頻繁k項集中支援度低於閾值的資料集,得到頻繁k項集。如果得到的頻繁k項集為空,則直接返回頻繁k-1項集的集合作為演算法結果,演算法結束。如果得到的頻繁k項集只有一項,則直接返回頻繁k項集的集合作為演算法結果,演算法結束。
c) 基於頻繁k項集,連線生成候選頻繁k+1項集。
3) 令k=k+1,轉入步驟2。
從演算法的步驟可以看出,Aprior演算法每輪迭代都要掃描資料集,因此在資料集很大,資料種類很多的時候,演算法效率很低。
4. Aprior演算法總結
Aprior演算法是一個非常經典的頻繁項集的挖掘演算法,很多演算法都是基於Aprior演算法而產生的,包括FP-Tree,GSP, CBA等。這些演算法利用了Aprior演算法的思想,但是對演算法做了改進,資料探勘效率更好一些,因此現在一般很少直接用Aprior演算法來挖掘資料了,但是理解Aprior演算法是理解其它Aprior類演算法的前提,同時演算法本身也不復雜,因此值得好好研究一番。
不過scikit-learn中並沒有頻繁集挖掘相關的演算法類庫,這不得不說是一個遺憾,不知道後面的版本會不會加上。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)