區域性線性嵌入(Locally Linear Embedding,以下簡稱LLE)也是非常重要的降維方法。和傳統的PCA,LDA等關注樣本方差的降維方法相比,LLE關注於降維時保持樣本區域性的線性特徵,由於LLE在降維時保持了樣本的區域性特徵,它廣泛的用於影象影象識別,高維資料視覺化等領域。下面我們就對LLE的原理做一個總結。
1. 流形學習概述
LLE屬於流形學習(Manifold Learning)的一種。因此我們首先看看什麼是流形學習。流形學習是一大類基於流形的框架。數學意義上的流形比較抽象,不過我們可以認為LLE中的流形是一個不閉合的曲面。這個流形曲面有資料分佈比較均勻,且比較稠密的特徵,有點像流水的味道。基於流行的降維演算法就是將流形從高維到低維的降維過程,在降維的過程中我們希望流形在高維的一些特徵可以得到保留。
一個形象的流形降維過程如下圖。我們有一塊捲起來的布,我們希望將其展開到一個二維平面,我們希望展開後的布能夠在區域性保持布結構的特徵,其實也就是將其展開的過程,就想兩個人將其拉開一樣。
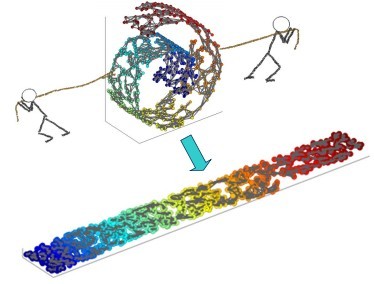
在區域性保持布結構的特徵,或者說資料特徵的方法有很多種,不同的保持方法對應不同的流形演算法。比如等距對映(ISOMAP)演算法在降維後希望保持樣本之間的測地距離而不是歐式距離,因為測地距離更能反映樣本之間在流形中的真實距離。
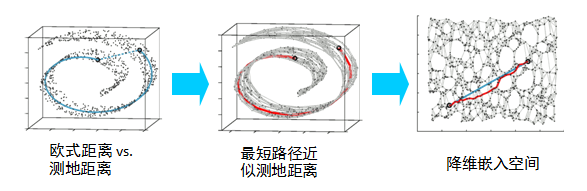
但是等距對映演算法有一個問題就是他要找所有樣本全域性的最優解,當資料量很大,樣本維度很高時,計算非常的耗時,鑑於這個問題,LLE通過放棄所有樣本全域性最優的降維,只是通過保證區域性最優來降維。同時假設樣本集在區域性是滿足線性關係的,進一步減少的降維的計算量。
2. LLE思想
現在我們來看看LLE的演算法思想。
LLE首先假設資料在較小的區域性是線性的,也就是說,某一個資料可以由它鄰域中的幾個樣本來線性表示。比如我們有一個樣本$x_1$,我們在它的原始高維鄰域裡用K-近鄰思想找到和它最近的三個樣本$x_2,x_3,x_4$. 然後我們假設$x_1$可以由$x_2,x_3,x_4$線性表示,即:$$x_1 = w_{12}x_2 + w_{13}x_3 +w_{14}x_4$$
其中,$w_{12}, w_{13}, w_{14}$為權重係數。在我們通過LLE降維後,我們希望$x_1$在低維空間對應的投影$x_1'$和$x_2,x_3,x_4$對應的投影$x_2',x_3',x_4'$也儘量保持同樣的線性關係,即$$x_1' \approx w_{12}x_2' + w_{13}x_3' +w_{14}x_4'$$
也就是說,投影前後線性關係的權重係數$w_{12}, w_{13}, w_{14}$是儘量不變或者最小改變的。
從上面可以看出,線性關係只在樣本的附近起作用,離樣本遠的樣本對區域性的線性關係沒有影響,因此降維的複雜度降低了很多。
下面我們推導LLE演算法的過程。
3. LLE演算法推導
對於LLE演算法,我們首先要確定鄰域大小的選擇,即我們需要多少個鄰域樣本來線性表示某個樣本。假設這個值為k。我們可以通過和KNN一樣的思想通過距離度量比如歐式距離來選擇某樣本的k個最近鄰。
在尋找到某個樣本的$x_i$的k個最近鄰之後我們就需要找到找到$x_i$和這k個最近鄰之間的線性關係,也就是要找到線性關係的權重係數。找線性關係,這顯然是一個迴歸問題。假設我們有m個n維樣本$\{x_1,x_2,...,x_m\}$,我們可以用均方差作為迴歸問題的損失函式:即:$$J(w) = \sum\limits_{i=1}^{m}||x_i-\sum\limits_{j \in Q(i)}w_{ij}x_j||_2^2$$
其中,$Q(i)$表示$i$的k個近鄰樣本集合。一般我們也會對權重係數$w_{ij}$做歸一化的限制,即權重係數需要滿足$$\sum\limits_{j \in Q(i)}w_{ij} = 1$$
對於不在樣本$x_i$鄰域內的樣本$x_j$,我們令對應的$w_{ij} = 0$,這樣可以把$w$擴充套件到整個資料集的維度。
也就是我們需要通過上面兩個式子求出我們的權重係數。一般我們可以通過矩陣和拉格朗日子乘法來求解這個最優化問題。
對於第一個式子,我們先將其矩陣化:$$ \begin{align} J(W) & = \sum\limits_{i=1}^{m}||x_i-\sum\limits_{j \in Q(i)}w_{ij}x_j||_2^2 \\& = \sum\limits_{i=1}^{m}||\sum\limits_{j \in Q(i)}w_{ij}x_i-\sum\limits_{j \in Q(i)}w_{ij}x_j||_2^2 \\& = \sum\limits_{i=1}^{m}||\sum\limits_{j \in Q(i)}w_{ij}(x_i-x_j)||_2^2 \\& = \sum\limits_{i=1}^{m} W_i^T(x_i-x_j)(x_i-x_j)^TW_i \end{align}$$
其中$W_i =(w_{i1}, w_{i2},...w_{ik})^T$。
我們令矩陣$Z_i=(x_i-x_j)(x_i-x_j)^T,j \in Q(i)$,則第一個式子進一步簡化為$J(W) = \sum\limits_{i=1}^{k} W_i^TZ_iW_i$.對於第二個式子,我們可以矩陣化為:$$\sum\limits_{j \in Q(i)}w_{ij} = W_i^T1_k = 1$$
其中$1_k$為k維全1向量。
現在我們將矩陣化的兩個式子用拉格朗日子乘法合為一個優化目標:$$L(W) = \sum\limits_{i=1}^{k} W_i^TZ_iW_i + \lambda(W_i^T1_k - 1)$$
對$W$求導並令其值為0,我們得到$$2Z_iW_i + \lambda1_k = 0$$
即我們的$$W_i = \lambda'Z_i^{-1}1_k$$
其中 $\lambda' = -\frac{1}{2}\lambda$為一個常數。利用 $W_i^T1_k = 1$,對$W_i$歸一化,那麼最終我們的權重係數$W_i$為:$$W_i = \frac{Z_i^{-1}1_k}{1_k^TZ_i^{-1}1_k}$$
現在我們得到了高維的權重係數,那麼我們希望這些權重係數對應的線性關係在降維後的低維一樣得到保持。假設我們的n維樣本集$\{x_1,x_2,...,x_m\}$在低維的d維度對應投影為$\{y_1,y_2,...,y_m\}$, 則我們希望保持線性關係,也就是希望對應的均方差損失函式最小,即最小化損失函式$J(Y)$如下:$$J(y) = \sum\limits_{i=1}^{m}||y_i-\sum\limits_{j=1}^{m}w_{ij}y_j||_2^2$$
可以看到這個式子和我們在高維的損失函式幾乎相同,唯一的區別是高維的式子中,高維資料已知,目標是求最小值對應的權重係數$W$,而我們在低維是權重係數$W$已知,求對應的低維資料。注意,這裡的$W$已經是$m \times m$維度,之前的$W$是$m \times k$維度,我們將那些不在鄰域位置的$W$的位置取值為0,將$W$擴充到$m \times m$維度。
為了得到標準化的低維資料,一般我們也會加入約束條件如下:$$\sum\limits_{i=1}^{m}y_i =0;\;\; \frac{1}{m}\sum\limits_{i=1}^{m}y_iy_i^T = I$$
首先我們將目標損失函式矩陣化:$$ \begin{align} J(Y) & = \sum\limits_{i=1}^{m}||y_i-\sum\limits_{j=1}^{m}w_{ij}y_j||_2^2 \\& = \sum\limits_{i=1}^{m}||YI_i-YW_i||_2^2 \\& = tr(Y(I-W)(I-W)^TY^T) \end{align}$$
如果我們令$M=(I-W)(I-W)^T$,則優化函式轉變為最小化下式:$J(Y) = tr(YMY^T)$,tr為跡函式。約束函式矩陣化為:$YY^T=mI$
如果大家熟悉譜聚類和PCA的優化,就會發現這裡的優化過程幾乎一樣。其實最小化J(Y)對應的Y就是M的最小的d個特徵值所對應的d個特徵向量組成的矩陣。當然我們也可以通過拉格朗日函式來得到這個:$$L(Y) = tr(YMY^T+\lambda(YY^T-mI))$$
對Y求導並令其為0,我們得到$2MY^T + 2\lambda Y^T =0$,即$MY^T = \lambda Y^T$,這樣我們就很清楚了,要得到最小的d維資料集,我們需要求出矩陣M最小的d個特徵值所對應的d個特徵向量組成的矩陣$Y=(y_1,y_2,...y_d)^T$即可。
一般的,由於M的最小特徵值為0不能反應資料特徵,此時對應的特徵向量為全1。我們通常選擇M的第2個到第d+1個最小的特徵值對應的特徵向量$M=(y_2,y_3,...y_{d+1})$來得到最終的Y。為什麼M的最小特徵值為0呢?這是因為$W^Te =e$, 得到$|W^T-I|e =0$,由於$e \neq 0$,所以只有$W^T-I =0$,即 $(I-W)^T=0$,兩邊同時左乘$I-W$,即可得到$(I-W)(I-W)^Te =0e$,即M的最小特徵值為0.
4. LLE演算法流程
在上一節我們已經基本推導了LLE降維的整個流程,現在我們對演算法過程做一個總結。整個LLE演算法用一張圖可以表示如下:
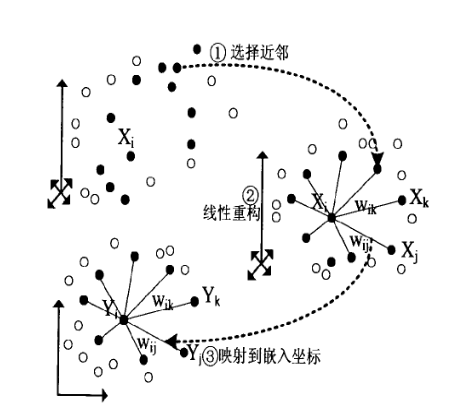
從圖中可以看出,LLE演算法主要分為三步,第一步是求K近鄰的過程,這個過程使用了和KNN演算法一樣的求最近鄰的方法。第二步,就是對每個樣本求它在鄰域裡的K個近鄰的線性關係,得到線性關係權重係數W,具體過程在第三節第一部分。第三步就是利用權重係數來在低維裡重構樣本資料,具體過程在第三節第二部分。
具體過程如下:
輸入:樣本集$D=\{x_1,x_2,...,x_m\}$, 最近鄰數k,降維到的維數d
輸出: 低維樣本集矩陣$D'$
1) for i 1 to m, 按歐式距離作為度量,計算和$x_i$最近的的k個最近鄰$(x_{i1}, x_{i2}, ...,x_{ik},)$
2) for i 1 to m, 求出區域性協方差矩陣$Z_i=(x_i-x_j)^T(x_i-x_j)$,並求出對應的權重係數向量:$$W_i = \frac{Z_i^{-1}1_k}{1_k^TZ_i^{-1}1_k}$$
3) 由權重係數向量$W_i$組成權重係數矩陣$W$,計算矩陣$M=(I-W)(I-W)^T$
4) 計算矩陣M的前d+1個特徵值,並計算這d+1個特徵值對應的特徵向量$\{y_1,y_2,...y_{d+1}\}$。
5)由第二個特徵向量到第d+1個特徵向量所張成的矩陣即為輸出低維樣本集矩陣$D' = (y_2,y_3,...y_{d+1})$
5. LLE的一些改進演算法
LLE演算法很簡單高效,但是卻有一些問題,比如如果近鄰數k大於輸入資料的維度時,我們的權重係數矩陣不是滿秩的。為了解決這樣類似的問題,有一些LLE的變種產生出來。比如:Modified Locally Linear Embedding(MLLE)和Hessian Based LLE(HLLE)。對於HLLE,它不是考慮保持區域性的線性關係,而是保持區域性的Hessian矩陣的二次型的關係。而對於MLLE,它對搜尋到的最近鄰的權重進行了度量,我們一般都是找距離最近的k個最近鄰就可以了,而MLLE在找距離最近的k個最近鄰的同時要考慮近鄰的分佈權重,它希望找到的近鄰的分佈權重儘量在樣本的各個方向,而不是集中在一側。
另一個比較好的LLE的變種是Local tangent space alignment(LTSA),它希望保持資料集區域性的幾何關係,在降維後希望區域性的幾何關係得以保持,同時利用了區域性幾何到整體性質過渡的技巧。
這些演算法原理都是基於LLE,基本都是在LLE這三步過程中尋求優化的方法。具體這裡就不多講了。
6. LLE總結
LLE是廣泛使用的圖形影象降維方法,它實現簡單,但是對資料的流形分佈特徵有嚴格的要求。比如不能是閉合流形,不能是稀疏的資料集,不能是分佈不均勻的資料集等等,這限制了它的應用。下面總結下LLE演算法的優缺點。
LLE演算法的主要優點有:
1)可以學習任意維的區域性線性的低維流形
2)演算法歸結為稀疏矩陣特徵分解,計算複雜度相對較小,實現容易。
LLE演算法的主要缺點有:
1)演算法所學習的流形只能是不閉合的,且樣本集是稠密均勻的。
2)演算法對最近鄰樣本數的選擇敏感,不同的最近鄰數對最後的降維結果有很大影響。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)