在主成分分析(PCA)原理總結中,我們對降維演算法PCA做了總結。這裡我們就對另外一種經典的降維方法線性判別分析(Linear Discriminant Analysis, 以下簡稱LDA)做一個總結。LDA在模式識別領域(比如人臉識別,艦艇識別等圖形影象識別領域)中有非常廣泛的應用,因此我們有必要了解下它的演算法原理。
在學習LDA之前,有必要將其自然語言處理領域的LDA區別開來,在自然語言處理領域, LDA是隱含狄利克雷分佈(Latent Dirichlet Allocation,簡稱LDA),他是一種處理文件的主題模型。我們本文只討論線性判別分析,因此後面所有的LDA均指線性判別分析。
1. LDA的思想
LDA是一種監督學習的降維技術,也就是說它的資料集的每個樣本是有類別輸出的。這點和PCA不同。PCA是不考慮樣本類別輸出的無監督降維技術。LDA的思想可以用一句話概括,就是“投影后類內方差最小,類間方差最大”。什麼意思呢? 我們要將資料在低維度上進行投影,投影后希望每一種類別資料的投影點儘可能的接近,而不同類別的資料的類別中心之間的距離儘可能的大。
可能還是有點抽象,我們先看看最簡單的情況。假設我們有兩類資料 分別為紅色和藍色,如下圖所示,這些資料特徵是二維的,我們希望將這些資料投影到一維的一條直線,讓每一種類別資料的投影點儘可能的接近,而紅色和藍色資料中心之間的距離儘可能的大。
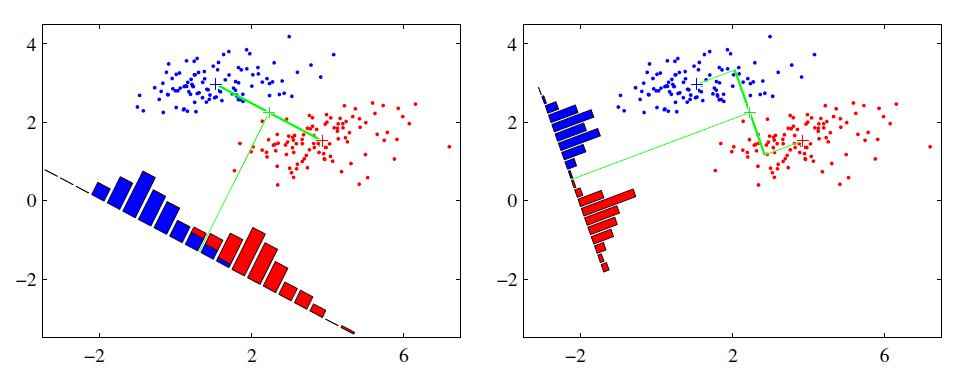
上圖中國提供了兩種投影方式,哪一種能更好的滿足我們的標準呢?從直觀上可以看出,右圖要比左圖的投影效果好,因為右圖的黑色資料和藍色資料各個較為集中,且類別之間的距離明顯。左圖則在邊界處資料混雜。以上就是LDA的主要思想了,當然在實際應用中,我們的資料是多個類別的,我們的原始資料一般也是超過二維的,投影后的也一般不是直線,而是一個低維的超平面。
在我們將上面直觀的內容轉化為可以度量的問題之前,我們先了解些必要的數學基礎知識,這些在後面講解具體LDA原理時會用到。
2. 瑞利商(Rayleigh quotient)與廣義瑞利商(genralized Rayleigh quotient)
我們首先來看看瑞利商的定義。瑞利商是指這樣的函式$R(A,x)$: $$R(A,x) = \frac{x^HAx}{x^Hx}$$
其中$x$為非零向量,而$A$為$n \times n$的Hermitan矩陣。所謂的Hermitan矩陣就是滿足共軛轉置矩陣和自己相等的矩陣,即$A^H=A$。如果我們的矩陣A是實矩陣,則滿足$A^T=A$的矩陣即為Hermitan矩陣。
瑞利商$R(A,x)$有一個非常重要的性質,即它的最大值等於矩陣$A$最大的特徵值,而最小值等於矩陣$A$的最小的特徵值,也就是滿足$$\lambda_{min} \leq \frac{x^HAx}{x^Hx} \leq \lambda_{max}$$
具體的證明這裡就不給出了。當向量$x$是標準正交基時,即滿足$x^Hx=1$時,瑞利商退化為:$R(A,x) = x^HAx$,這個形式在譜聚類和PCA中都有出現。
以上就是瑞利商的內容,現在我們再看看廣義瑞利商。廣義瑞利商是指這樣的函式$R(A,B,x)$: $$R(A,x) = \frac{x^HAx}{x^HBx}$$
其中$x$為非零向量,而$A,B$為$n \times n$的Hermitan矩陣。$B$為正定矩陣。它的最大值和最小值是什麼呢?其實我們只要通過將其通過標準化就可以轉化為瑞利商的格式。我們令$x=B^{-1/2}x'$,則分母轉化為:$$x^HBx = x'^H(B^{-1/2})^HBB^{-1/2}x' = x'^HB^{-1/2}BB^{-1/2}x' = x'^Hx'$$
而分子轉化為:$$x^HAx = x'^HB^{-1/2}AB^{-1/2}x' $$
此時我們的$R(A,B,x)$轉化為$R(A,B,x')$:$$R(A,B,x') = \frac{x'^HB^{-1/2}AB^{-1/2}x'}{x'^Hx'}$$
利用前面的瑞利商的性質,我們可以很快的知道,$R(A,B,x)$的最大值為矩陣$B^{-1/2}AB^{-1/2}$的最大特徵值,或者說矩陣$B^{-1}A$的最大特徵值,而最小值為矩陣$B^{-1}A$的最小特徵值。如果你看過我寫的譜聚類(spectral clustering)原理總結第6.2節的話,就會發現這裡使用了一樣的技巧,即對矩陣進行標準化。
3. 二類LDA原理
現在我們回到LDA的原理上,我們在第一節說講到了LDA希望投影后希望同一種類別資料的投影點儘可能的接近,而不同類別的資料的類別中心之間的距離儘可能的大,但是這只是一個感官的度量。現在我們首先從比較簡單的二類LDA入手,嚴謹的分析LDA的原理。
假設我們的資料集$D=\{(x_1,y_1), (x_2,y_2), ...,((x_m,y_m))\}$,其中任意樣本$x_i$為n維向量,$y_i \in \{0,1\}$。我們定義$N_j(j=0,1)$為第j類樣本的個數,$X_j(j=0,1)$為第j類樣本的集合,而$\mu_j(j=0,1)$為第j類樣本的均值向量,定義$\Sigma_j(j=0,1)$為第j類樣本的協方差矩陣(嚴格說是缺少分母部分的協方差矩陣)。
$\mu_j$的表示式為:$$\mu_j = \frac{1}{N_j}\sum\limits_{x \in X_j}x\;\;(j=0,1)$$
$\Sigma_j$的表示式為:$$\Sigma_j = \sum\limits_{x \in X_j}(x-\mu_j)(x-\mu_j)^T\;\;(j=0,1)$$
由於是兩類資料,因此我們只需要將資料投影到一條直線上即可。假設我們的投影直線是向量$w$,則對任意一個樣本本$x_i$,它在直線$w$的投影為$w^Tx_i$,對於我們的兩個類別的中心點$\mu_0,\mu_1$,在在直線$w$的投影為$w^T\mu_0$和$w^T\mu_1$。由於LDA需要讓不同類別的資料的類別中心之間的距離儘可能的大,也就是我們要最大化$||w^T\mu_0-w^T\mu_1||_2^2$,同時我們希望同一種類別資料的投影點儘可能的接近,也就是要同類樣本投影點的協方差$w^T\Sigma_0w$和$w^T\Sigma_1w$儘可能的小,即最小化$w^T\Sigma_0w+w^T\Sigma_1w$。綜上所述,我們的優化目標為:$$\underbrace{arg\;max}_w\;\;J(w) = \frac{||w^T\mu_0-w^T\mu_1||_2^2}{w^T\Sigma_0w+w^T\Sigma_1w} = \frac{w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw}{w^T(\Sigma_0+\Sigma_1)w}$$
我們一般定義類內散度矩陣$S_w$為:$$S_w = \Sigma_0 + \Sigma_1 = \sum\limits_{x \in X_0}(x-\mu_0)(x-\mu_0)^T + \sum\limits_{x \in X_1}(x-\mu_1)(x-\mu_1)^T$$
同時定義類間散度矩陣$S_b$為:$$S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T$$
這樣我們的優化目標重寫為:$$\underbrace{arg\;max}_w\;\;J(w) = \frac{w^TS_bw}{w^TS_ww} $$
仔細一看上式,這不就是我們的廣義瑞利商嘛!這就簡單了,利用我們第二節講到的廣義瑞利商的性質,我們知道我們的$J(w)$最大值為矩陣$S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w$的最大特徵值,而對應的$w$為$S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w$的最大特徵值對應的特徵向量! 而$S_w^{-1}S_b$的特徵值和$S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w$的特徵值相同,$S_w^{-1}S_b$的特徵向量$w'$和$S^{−\frac{1}{2}}_wS_bS^{−\frac{1}{2}}_w$的特徵向量$w$滿足$w' = S^{−\frac{1}{2}}_ww$的關係!
注意到對於二類的時候,$S_bw'$的方向恆為$\mu_0-\mu_1$,不妨令$S_bw'=\lambda(\mu_0-\mu_1)$,將其帶入:$(S_w^{-1}S_b)w'=\lambda w'$,可以得到$w'=S_w^{-1}(\mu_0-\mu_1)$, 也就是說我們只要求出原始二類樣本的均值和方差就可以確定最佳的投影方向$w$了。
4. 多類LDA原理
有了二類LDA的基礎,我們再來看看多類別LDA的原理。
假設我們的資料集$D=\{(x_1,y_1), (x_2,y_2), ...,((x_m,y_m))\}$,其中任意樣本$x_i$為n維向量,$y_i \in \{C_1,C_2,...,C_k\}$。我們定義$N_j(j=1,2...k)$為第j類樣本的個數,$X_j(j=1,2...k)$為第j類樣本的集合,而$\mu_j(j=1,2...k)$為第j類樣本的均值向量,定義$\Sigma_j(j=1,2...k)$為第j類樣本的協方差矩陣。在二類LDA裡面定義的公式可以很容易的類推到多類LDA。
由於我們是多類向低維投影,則此時投影到的低維空間就不是一條直線,而是一個超平面了。假設我們投影到的低維空間的維度為d,對應的基向量為$(w_1,w_2,...w_d)$,基向量組成的矩陣為$W$, 它是一個$n \times d$的矩陣。
此時我們的優化目標應該可以變成為:$$\frac{W^TS_bW}{W^TS_wW}$$
其中$S_b = \sum\limits_{j=1}^{k}N_j(\mu_j-\mu)(\mu_j-\mu)^T$,$\mu$為所有樣本均值向量。$S_w = \sum\limits_{j=1}^{k}S_{wj} = \sum\limits_{j=1}^{k}\sum\limits_{x \in X_j}(x-\mu_j)(x-\mu_j)^T$
但是有一個問題,就是$W^TS_bW$和$W^TS_wW$都是矩陣,不是標量,無法作為一個標量函式來優化!也就是說,我們無法直接用二類LDA的優化方法,怎麼辦呢?一般來說,我們可以用其他的一些替代優化目標來實現。
常見的一個LDA多類優化目標函式定義為:$$\underbrace{arg\;max}_W\;\;J(W) = \frac{\prod\limits_{diag}W^TS_bW}{\prod\limits_{diag}W^TS_wW}$$
其中$\prod\limits_{diag}A$為$A$的主對角線元素的乘積,$W$為$n \times d$的矩陣。
$J(W)$的優化過程可以轉化為:$$J(W) = \frac{\prod\limits_{i=1}^dw_i^TS_bw_i}{\prod\limits_{i=1}^dw_i^TS_ww_i} = \prod\limits_{i=1}^d\frac{w_i^TS_bw_i}{w_i^TS_ww_i}$$
仔細觀察上式最右邊,這不就是廣義瑞利商嘛!最大值是矩陣$S_w^{-1}S_b$的最大特徵值,最大的d個值的乘積就是矩陣$S_w^{-1}S_b$的最大的d個特徵值的乘積,此時對應的矩陣$W$為這最大的d個特徵值對應的特徵向量張成的矩陣。
由於$W$是一個利用了樣本的類別得到的投影矩陣,因此它的降維到的維度d最大值為k-1。為什麼最大維度不是類別數k呢?因為$S_b$中每個$\mu_j-\mu$的秩為1,因此協方差矩陣相加後最大的秩為k(矩陣的秩小於等於各個相加矩陣的秩的和),但是由於如果我們知道前k-1個$\mu_j$後,最後一個$\mu_k$可以由前k-1個$\mu_j$線性表示,因此$S_b$的秩最大為k-1,即特徵向量最多有k-1個。
5. LDA演算法流程
在第三節和第四節我們講述了LDA的原理,現在我們對LDA降維的流程做一個總結。
輸入:資料集$D=\{(x_1,y_1), (x_2,y_2), ...,((x_m,y_m))\}$,其中任意樣本$x_i$為n維向量,$y_i \in \{C_1,C_2,...,C_k\}$,降維到的維度d。
輸出:降維後的樣本集$D′$
1) 計算類內散度矩陣$S_w$
2) 計算類間散度矩陣$S_b$
3) 計算矩陣$S_w^{-1}S_b$
4)計算$S_w^{-1}S_b$的最大的d個特徵值和對應的d個特徵向量$(w_1,w_2,...w_d)$,得到投影矩陣W$W$
5) 對樣本集中的每一個樣本特徵$x_i$,轉化為新的樣本$z_i=W^Tx_i$
6) 得到輸出樣本集$D'=\{(z_1,y_1), (z_2,y_2), ...,((z_m,y_m))\}$
以上就是使用LDA進行降維的演算法流程。實際上LDA除了可以用於降維以外,還可以用於分類。一個常見的LDA分類基本思想是假設各個類別的樣本資料符合高斯分佈,這樣利用LDA進行投影后,可以利用極大似然估計計算各個類別投影資料的均值和方差,進而得到該類別高斯分佈的概率密度函式。當一個新的樣本到來後,我們可以將它投影,然後將投影后的樣本特徵分別帶入各個類別的高斯分佈概率密度函式,計算它屬於這個類別的概率,最大的概率對應的類別即為預測類別。
由於LDA應用於分類現在似乎也不是那麼流行,至少我們公司裡沒有用過,這裡我就不多講了。
6. LDA vs PCA
LDA用於降維,和PCA有很多相同,也有很多不同的地方,因此值得好好的比較一下兩者的降維異同點。
首先我們看看相同點:
1)兩者均可以對資料進行降維。
2)兩者在降維時均使用了矩陣特徵分解的思想。
3)兩者都假設資料符合高斯分佈。
我們接著看看不同點:
1)LDA是有監督的降維方法,而PCA是無監督的降維方法
2)LDA降維最多降到類別數k-1的維數,而PCA沒有這個限制。
3)LDA除了可以用於降維,還可以用於分類。
4)LDA選擇分類效能最好的投影方向,而PCA選擇樣本點投影具有最大方差的方向。
這點可以從下圖形象的看出,在某些資料分佈下LDA比PCA降維較優。

當然,某些某些資料分佈下PCA比LDA降維較優,如下圖所示:
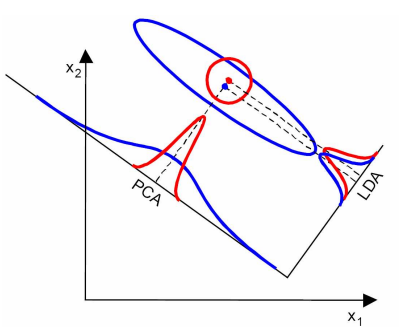
7. LDA演算法小結
LDA演算法既可以用來降維,又可以用來分類,但是目前來說,主要還是用於降維。在我們進行影象識別影象識別相關的資料分析時,LDA是一個有力的工具。下面總結下LDA演算法的優缺點。
LDA演算法的主要優點有:
1)在降維過程中可以使用類別的先驗知識經驗,而像PCA這樣的無監督學習則無法使用類別先驗知識。
2)LDA在樣本分類資訊依賴均值而不是方差的時候,比PCA之類的演算法較優。
LDA演算法的主要缺點有:
1)LDA不適合對非高斯分佈樣本進行降維,PCA也有這個問題。
2)LDA降維最多降到類別數k-1的維數,如果我們降維的維度大於k-1,則不能使用LDA。當然目前有一些LDA的進化版演算法可以繞過這個問題。
3)LDA在樣本分類資訊依賴方差而不是均值的時候,降維效果不好。
4)LDA可能過度擬合資料。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)