在BIRCH聚類演算法原理中,我們對BIRCH聚類演算法的原理做了總結,本文就對scikit-learn中BIRCH演算法的使用做一個總結。
1. scikit-learn之BIRCH類
在scikit-learn中,BIRCH類實現了原理篇裡講到的基於特徵樹CF Tree的聚類。因此要使用BIRCH來聚類,關鍵是對CF Tree結構引數的處理。
在CF Tree中,幾個關鍵的引數為內部節點的最大CF數B, 葉子節點的最大CF數L, 葉節點每個CF的最大樣本半徑閾值T。這三個引數定了,CF Tree的結構也基本確定了,最後的聚類效果也基本確定。可以說BIRCH的調參就是除錯B,L和T。
至於類別數K,此時反而是可選的,不輸入K,則BIRCH會對CF Tree裡各葉子節點CF中樣本的情況自己決定類別數K值,如果輸入K值,則BIRCH會CF Tree裡各葉子節點CF進行合併,直到類別數為K。
2. BIRCH類引數
在scikit-learn中,BIRCH類的重要引數不多,下面一併講解。
1) threshold:即葉節點每個CF的最大樣本半徑閾值T,它決定了每個CF裡所有樣本形成的超球體的半徑閾值。一般來說threshold越小,則CF Tree的建立階段的規模會越大,即BIRCH演算法第一階段所花的時間和記憶體會越多。但是選擇多大以達到聚類效果則需要通過調參決定。預設值是0.5.如果樣本的方差較大,則一般需要增大這個預設值。
2) branching_factor:即CF Tree內部節點的最大CF數B,以及葉子節點的最大CF數L。這裡scikit-learn對這兩個引數進行了統一取值。也就是說,branching_factor決定了CF Tree裡所有節點的最大CF數。預設是50。如果樣本量非常大,比如大於10萬,則一般需要增大這個預設值。選擇多大的branching_factor以達到聚類效果則需要通過和threshold一起調參決定
3)n_clusters:即類別數K,在BIRCH演算法是可選的,如果類別數非常多,我們也沒有先驗知識,則一般輸入None,此時BIRCH演算法第4階段不會執行。但是如果我們有類別的先驗知識,則推薦輸入這個可選的類別值。預設是3,即最終聚為3類。
4)compute_labels:布林值,表示是否標示類別輸出,預設是True。一般使用預設值挺好,這樣可以看到聚類效果。
在評估各個引數組合的聚類效果時,還是推薦使用Calinski-Harabasz Index,Calinski-Harabasz Index在scikit-learn中對應的方法是metrics.calinski_harabaz_score.
3. BIRCH運用例項
這裡我們用一個例子來學習BIRCH演算法。完整程式碼參見我的github:https://github.com/ljpzzz/machinelearning/blob/master/classic-machine-learning/birch_cluster.ipynb
首先,我們載入一些隨機資料,並看看資料的分佈圖:
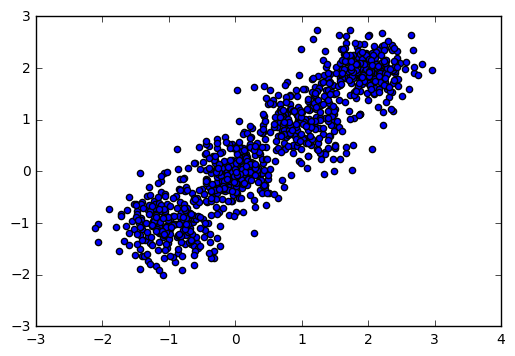
import numpy as np import matplotlib.pyplot as plt %matplotlib inline from sklearn.datasets.samples_generator import make_blobs # X為樣本特徵,Y為樣本簇類別, 共1000個樣本,每個樣本2個特徵,共4個簇,簇中心在[-1,-1], [0,0],[1,1], [2,2] X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.3, 0.4, 0.3], random_state =9) plt.scatter(X[:, 0], X[:, 1], marker='o') plt.show()
輸出圖如下:
現在我們用BIRCH演算法來聚類,首先我們選擇不輸入可選的類別數K,看看聚類效果和Calinski-Harabasz 分數。
from sklearn.cluster import Birch y_pred = Birch(n_clusters = None).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show() from sklearn import metrics print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
輸出圖如下:
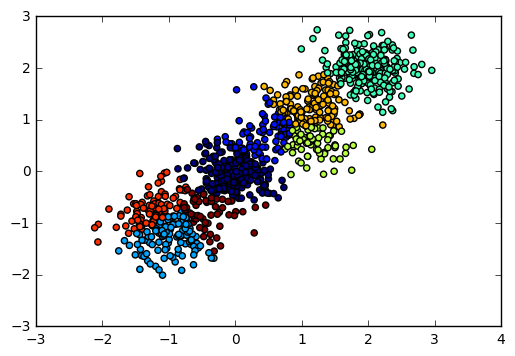
對應的Calinski-Harabasz 分數輸出為:
Calinski-Harabasz Score 2220.95253905
由於我們知道資料是4個簇隨機產生的,因此我們可以通過輸入可選的類別數4來看看BIRCH聚類的輸出。程式碼如下:
y_pred = Birch(n_clusters = 4).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show() print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
輸出圖如下:
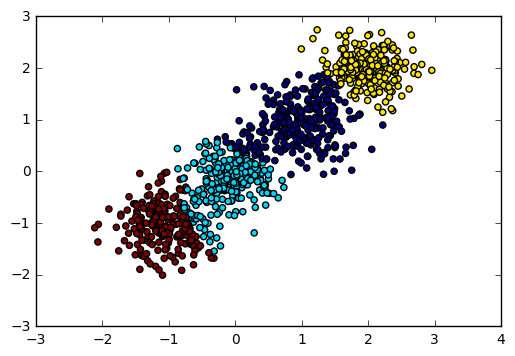
對應的Calinski-Harabasz 分數輸出為:
Calinski-Harabasz Score 2816.40765268
可見如果我們不輸入類別數的話,在某些時候BIRCH演算法的聚類效果並不一定好,因此這個可選的類別數K一般還是需要調參的。
對於threshold和branching_factor我們前面還沒有去調參,使用了預設的threshold值0.5和預設的branching_factor值50.
現在我們將threshold從0.5降低為0.3,讓BIRCH演算法第一階段的CF Tree規模變大,並觀察Calinski-Harabasz 分數。
y_pred = Birch(n_clusters = 4, threshold = 0.3).fit_predict(X) print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
對應的Calinski-Harabasz 分數輸出為:
Calinski-Harabasz Score 3295.63492273
可見此時的聚類效果有了進一步的提升,那麼是不是threshold越小越好呢?我們看看threshold從0.3降低為0.1時的情況。
y_pred = Birch(n_clusters = 4, threshold = 0.1).fit_predict(X) print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
對應的Calinski-Harabasz 分數輸出為:
Calinski-Harabasz Score 2155.10021808
也就是說threshold不是越小聚類效果越好。
我們基於threshold為0.3的情況,除錯下branching_factor,將branching_factor從50降低為20.讓BIRCH演算法第一階段的CF Tree規模變大。
y_pred = Birch(n_clusters = 4, threshold = 0.3, branching_factor = 20).fit_predict(X) print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
對應的Calinski-Harabasz 分數輸出為:
Calinski-Harabasz Score 3301.80231064
可見除錯branching_factor也可以讓聚類分數提高。那麼和threshold類似,是不是branching_factor越小越好呢?我們將branching_factor從20降低為10,觀察聚類分數:
y_pred = Birch(n_clusters = 4, threshold = 0.3, branching_factor = 10).fit_predict(X) print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
對應的Calinski-Harabasz 分數輸出為:
Calinski-Harabasz Score 2800.87840962
也就是說和threshold類似,branching_factor不是越小聚類效果越好,需要調參。
以上就是BIRCH演算法的一些經驗,希望可以幫到朋友們。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)