在K近鄰法(KNN)原理小結這篇文章,我們討論了KNN的原理和優缺點,這裡我們就從實踐出發,對scikit-learn 中KNN相關的類庫使用做一個小結。主要關注於類庫調參時的一個經驗總結。
1. scikit-learn 中KNN相關的類庫概述
在scikit-learn 中,與近鄰法這一大類相關的類庫都在sklearn.neighbors包之中。KNN分類樹的類是KNeighborsClassifier,KNN迴歸樹的類是KNeighborsRegressor。除此之外,還有KNN的擴充套件,即限定半徑最近鄰分類樹的類RadiusNeighborsClassifier和限定半徑最近鄰迴歸樹的類RadiusNeighborsRegressor, 以及最近質心分類演算法NearestCentroid。
在這些演算法中,KNN分類和迴歸的類引數完全一樣。限定半徑最近鄰法分類和迴歸的類的主要引數也和KNN基本一樣。
比較特別是的最近質心分類演算法,由於它是直接選擇最近質心來分類,所以僅有兩個引數,距離度量和特徵選擇距離閾值,比較簡單,因此後面就不再專門講述最近質心分類演算法的引數。
另外幾個在sklearn.neighbors包中但不是做分類迴歸預測的類也值得關注。kneighbors_graph類返回用KNN時和每個樣本最近的K個訓練集樣本的位置。radius_neighbors_graph返回用限定半徑最近鄰法時和每個樣本在限定半徑內的訓練集樣本的位置。NearestNeighbors是個大雜燴,它即可以返回用KNN時和每個樣本最近的K個訓練集樣本的位置,也可以返回用限定半徑最近鄰法時和每個樣本最近的訓練集樣本的位置,常常用在聚類模型中。
2. K近鄰法和限定半徑最近鄰法類庫引數小結
本節對K近鄰法和限定半徑最近鄰法類庫引數做一個總結。包括KNN分類樹的類KNeighborsClassifier,KNN迴歸樹的類KNeighborsRegressor, 限定半徑最近鄰分類樹的類RadiusNeighborsClassifier和限定半徑最近鄰迴歸樹的類RadiusNeighborsRegressor。這些類的重要引數基本相同,因此我們放到一起講。
| 引數 | KNeighborsClassifier | KNeighborsRegressor | RadiusNeighborsClassifier | RadiusNeighborsRegressor |
|
KNN中的K值n_neighbors |
K值的選擇與樣本分佈有關,一般選擇一個較小的K值,可以通過交叉驗證來選擇一個比較優的K值,預設值是5。如果資料是三維一下的,如果資料是三維或者三維以下的,可以通過視覺化觀察來調參。 | 不適用於限定半徑最近鄰法 | ||
|
限定半徑最近鄰法中的半radius |
不適用於KNN | 半徑的選擇與樣本分佈有關,可以通過交叉驗證來選擇一個較小的半徑,儘量保證每類訓練樣本其他類別樣本的距離較遠,預設值是1.0。如果資料是三維或者三維以下的,可以通過視覺化觀察來調參。 | ||
|
近鄰權weights |
主要用於標識每個樣本的近鄰樣本的權重,如果是KNN,就是K個近鄰樣本的權重,如果是限定半徑最近鄰,就是在距離在半徑以內的近鄰樣本的權重。可以選擇"uniform","distance" 或者自定義權重。選擇預設的"uniform",意味著所有最近鄰樣本權重都一樣,在做預測時一視同仁。如果是"distance",則權重和距離成反比例,即距離預測目標更近的近鄰具有更高的權重,這樣在預測類別或者做迴歸時,更近的近鄰所佔的影響因子會更加大。當然,我們也可以自定義權重,即自定義一個函式,輸入是距離值,輸出是權重值。這樣我們可以自己控制不同的距離所對應的權重。 一般來說,如果樣本的分佈是比較成簇的,即各類樣本都在相對分開的簇中時,我們用預設的"uniform"就可以了,如果樣本的分佈比較亂,規律不好尋找,選擇"distance"是一個比較好的選擇。如果用"distance"發現預測的效果的還是不好,可以考慮自定義距離權重來調優這個引數。 |
|||
|
KNN和限定半徑最近鄰法使用的演算法algorithm |
演算法一共有三種,第一種是蠻力實現,第二種是KD樹實現,第三種是球樹實現。這三種方法在K近鄰法(KNN)原理小結中都有講述,如果不熟悉可以去複習下。對於這個引數,一共有4種可選輸入,‘brute’對應第一種蠻力實現,‘kd_tree’對應第二種KD樹實現,‘ball_tree’對應第三種的球樹實現, ‘auto’則會在上面三種演算法中做權衡,選擇一個擬合最好的最優演算法。需要注意的是,如果輸入樣本特徵是稀疏的時候,無論我們選擇哪種演算法,最後scikit-learn都會去用蠻力實現‘brute’。 個人的經驗,如果樣本少特徵也少,使用預設的 ‘auto’就夠了。 如果資料量很大或者特徵也很多,用"auto"建樹時間會很長,效率不高,建議選擇KD樹實現‘kd_tree’,此時如果發現‘kd_tree’速度比較慢或者已經知道樣本分佈不是很均勻時,可以嘗試用‘ball_tree’。而如果輸入樣本是稀疏的,無論你選擇哪個演算法最後實際執行的都是‘brute’。 |
|||
|
停止建子樹的葉子節點閾值leaf_size |
這個值控制了使用KD樹或者球樹時, 停止建子樹的葉子節點數量的閾值。這個值越小,則生成的KD樹或者球樹就越大,層數越深,建樹時間越長,反之,則生成的KD樹或者球樹會小,層數較淺,建樹時間較短。預設是30. 這個值一般依賴於樣本的數量,隨著樣本數量的增加,這個值必須要增加,否則不光建樹預測的時間長,還容易過擬合。可以通過交叉驗證來選擇一個適中的值。 如果使用的演算法是蠻力實現,則這個引數可以忽略。 |
|||
|
距離度量metric |
K近鄰法和限定半徑最近鄰法類可以使用的距離度量較多,一般來說預設的歐式距離(即p=2的閔可夫斯基距離)就可以滿足我們的需求。可以使用的距離度量引數有: a) 歐式距離 “euclidean”: $ \sqrt{\sum\limits_{i=1}^{n}(x_i-y_i)^2} $ b) 曼哈頓距離 “manhattan”: $ \sum\limits_{i=1}^{n}|x_i-y_i| $ c) 切比雪夫距離“chebyshev”: $ max|x_i-y_i| (i = 1,2,...n)$ d) 閔可夫斯基距離 “minkowski”(預設引數): $ \sqrt[p]{\sum\limits_{i=1}^{n}(|x_i-y_i|)^p} $ p=1為曼哈頓距離, p=2為歐式距離。 e) 帶權重閔可夫斯基距離 “wminkowski”: $ \sqrt[p]{\sum\limits_{i=1}^{n}(w*|x_i-y_i|)^p} $ 其中w為特徵權重 f) 標準化歐式距離 “seuclidean”: 即對於各特徵維度做了歸一化以後的歐式距離。此時各樣本特徵維度的均值為0,方差為1. g) 馬氏距離“mahalanobis”:$\sqrt{(x-y)^TS^{-1}(x-y)}$ 其中,$S^{-1}$為樣本協方差矩陣的逆矩陣。當樣本分佈獨立時, S為單位矩陣,此時馬氏距離等同於歐式距離 還有一些其他不是實數的距離度量,一般在KNN之類的演算法用不上,這裡也就不列了。 |
|||
|
距離度量附屬引數p |
p是使用距離度量引數 metric 附屬引數,只用於閔可夫斯基距離和帶權重閔可夫斯基距離中p值的選擇,p=1為曼哈頓距離, p=2為歐式距離。預設為2 | |||
|
距離度量其他附屬引數metric_params |
一般都用不上,主要是用於帶權重閔可夫斯基距離的權重,以及其他一些比較複雜的距離度量的引數。 | |||
|
並行處理任務數n_jobs |
主要用於多核CPU時的並行處理,加快建立KNN樹和預測搜尋的速度。一般用預設的-1就可以了,即所有的CPU核都參與計算。 | 不適用於限定半徑最近鄰法 | ||
| 異常點類別選擇outlier_label | 不適用於KNN | 主要用於預測時,如果目標點半徑內沒有任何訓練集的樣本點時,應該標記的類別,不建議選擇預設值 none,因為這樣遇到異常點會報錯。一般設定為訓練集裡最多樣本的類別。 | 不適用於限定半徑最近鄰迴歸 | |
3. 使用KNeighborsClassifier做分類的例項
完整程式碼見我的github: https://github.com/ljpzzz/machinelearning/blob/master/classic-machine-learning/knn_classifier.ipynb
3.1 生成隨機資料
首先,我們生成我們分類的資料,程式碼如下:
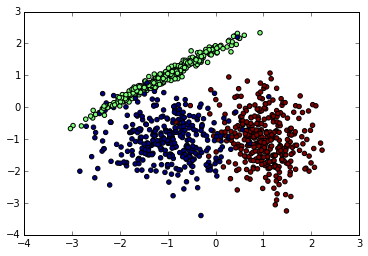
import numpy as np import matplotlib.pyplot as plt %matplotlib inline from sklearn.datasets.samples_generator import make_classification # X為樣本特徵,Y為樣本類別輸出, 共1000個樣本,每個樣本2個特徵,輸出有3個類別,沒有冗餘特徵,每個類別一個簇 X, Y = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_clusters_per_class=1, n_classes=3) plt.scatter(X[:, 0], X[:, 1], marker='o', c=Y) plt.show()
先看看我們生成的資料圖如下。由於是隨機生成,如果你也跑這段程式碼,生成的隨機資料分佈會不一樣。下面是我某次跑出的原始資料圖。
接著我們用KNN來擬合模型,我們選擇K=15,權重為距離遠近。程式碼如下:
from sklearn import neighbors clf = neighbors.KNeighborsClassifier(n_neighbors = 15 , weights='distance') clf.fit(X, Y)
最後,我們視覺化一下看看我們預測的效果如何,程式碼如下:
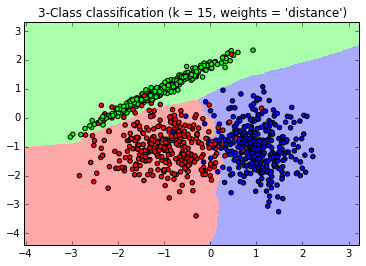
from matplotlib.colors import ListedColormap cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF']) #確認訓練集的邊界 x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #生成隨機資料來做測試集,然後作預測 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02)) Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # 畫出測試集資料 Z = Z.reshape(xx.shape) plt.figure() plt.pcolormesh(xx, yy, Z, cmap=cmap_light) # 也畫出所有的訓練集資料 plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=cmap_bold) plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.title("3-Class classification (k = 15, weights = 'distance')" )
生成的圖如下,可以看到大多數資料擬合不錯,僅有少量的異常點不在範圍內。
以上就是使用scikit-learn的KNN相關類庫的一個總結,希望可以幫到朋友們。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)