條件隨機場CRF(一)從隨機場到線性鏈條件隨機場
條件隨機場(Conditional Random Fields, 以下簡稱CRF)是給定一組輸入序列條件下另一組輸出序列的條件概率分佈模型,在自然語言處理中得到了廣泛應用。本系列主要關注於CRF的特殊形式:線性鏈(Linear chain) CRF。本文關注與CRF的模型基礎。
1.什麼樣的問題需要CRF模型
和HMM類似,在討論CRF之前,我們來看看什麼樣的問題需要CRF模型。這裡舉一個簡單的例子:
假設我們有Bob一天從早到晚的一系列照片,Bob想考考我們,要我們猜這一系列的每張照片對應的活動,比如: 工作的照片,吃飯的照片,唱歌的照片等等。一個比較直觀的辦法就是,我們找到Bob之前的日常生活的一系列照片,然後找Bob問清楚這些照片代表的活動標記,這樣我們就可以用監督學習的方法來訓練一個分類模型,比如邏輯迴歸,接著用模型去預測這一天的每張照片最可能的活動標記。
這種辦法雖然是可行的,但是卻忽略了一個重要的問題,就是這些照片之間的順序其實是有很大的時間順序關係的,而用上面的方法則會忽略這種關係。比如我們現在看到了一張Bob閉著嘴的照片,那麼這張照片我們怎麼標記Bob的活動呢?比較難去打標記。但是如果我們有Bob在這一張照片前一點點時間的照片的話,那麼這張照片就好標記了。如果在時間序列上前一張的照片裡Bob在吃飯,那麼這張閉嘴的照片很有可能是在吃飯咀嚼。而如果在時間序列上前一張的照片裡Bob在唱歌,那麼這張閉嘴的照片很有可能是在唱歌。
為了讓我們的分類器表現的更好,可以在標記資料的時候,可以考慮相鄰資料的標記資訊。這一點,是普通的分類器難以做到的。而這一塊,也是CRF比較擅長的地方。
在實際應用中,自然語言處理中的詞性標註(POS Tagging)就是非常適合CRF使用的地方。詞性標註的目標是給出一個句子中每個詞的詞性(名詞,動詞,形容詞等)。而這些詞的詞性往往和上下文的詞的詞性有關,因此,使用CRF來處理是很適合的,當然CRF不是唯一的選擇,也有很多其他的詞性標註方法。
2. 從隨機場到馬爾科夫隨機場
首先,我們來看看什麼是隨機場。“隨機場”的名字取的很玄乎,其實理解起來不難。隨機場是由若干個位置組成的整體,當給每一個位置中按照某種分佈隨機賦予一個值之後,其全體就叫做隨機場。還是舉詞性標註的例子:假如我們有一個十個詞形成的句子需要做詞性標註。這十個詞每個詞的詞性可以在我們已知的詞性集合(名詞,動詞...)中去選擇。當我們為每個詞選擇完詞性後,這就形成了一個隨機場。
瞭解了隨機場,我們再來看看馬爾科夫隨機場。馬爾科夫隨機場是隨機場的特例,它假設隨機場中某一個位置的賦值僅僅與和它相鄰的位置的賦值有關,和與其不相鄰的位置的賦值無關。繼續舉十個詞的句子詞性標註的例子: 如果我們假設所有詞的詞性只和它相鄰的詞的詞性有關時,這個隨機場就特化成一個馬爾科夫隨機場。比如第三個詞的詞性除了與自己本身的位置有關外,只與第二個詞和第四個詞的詞性有關。
3. 從馬爾科夫隨機場到條件隨機場
理解了馬爾科夫隨機場,再理解CRF就容易了。CRF是馬爾科夫隨機場的特例,它假設馬爾科夫隨機場中只有$X$和$Y$兩種變數,$X$一般是給定的,而$Y$一般是在給定$X$的條件下我們的輸出。這樣馬爾科夫隨機場就特化成了條件隨機場。在我們十個詞的句子詞性標註的例子中,$X$是詞,$Y$是詞性。因此,如果我們假設它是一個馬爾科夫隨機場,那麼它也就是一個CRF。
對於CRF,我們給出準確的數學語言描述:
設$X$與$Y$是隨機變數,$P(Y|X)$是給定$X$時$Y$的條件概率分佈,若隨機變數$Y$構成的是一個馬爾科夫隨機場,則稱條件概率分佈$P(Y|X)$是條件隨機場。
4. 從條件隨機場到線性鏈條件隨機場
注意在CRF的定義中,我們並沒有要求$X$和$Y$有相同的結構。而實現中,我們一般都假設$X$和$Y$有相同的結構,即:$$X =(X_1,X_2,...X_n),\;\;Y=(Y_1,Y_2,...Y_n)$$
我們一般考慮如下圖所示的結構:$X$和$Y$有相同的結構的CRF就構成了線性鏈條件隨機場(Linear chain Conditional Random Fields,以下簡稱 linear-CRF)。
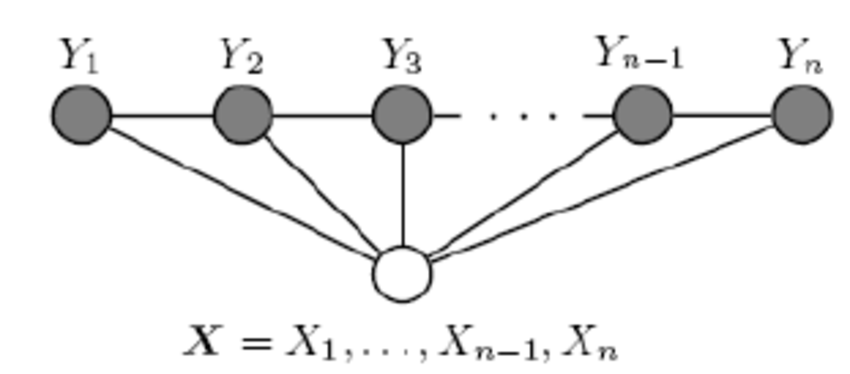
在我們的十個詞的句子的詞性標記中,詞有十個,詞性也是十個,因此,如果我們假設它是一個馬爾科夫隨機場,那麼它也就是一個linear-CRF。
我們再來看看 linear-CRF的數學定義:
設$X =(X_1,X_2,...X_n),\;\;Y=(Y_1,Y_2,...Y_n)$均為線性連結串列示的隨機變數序列,在給定隨機變數序列$X$的情況下,隨機變數$Y$的條件概率分佈$P(Y|X)$構成條件隨機場,即滿足馬爾科夫性:$$P(Y_i|X,Y_1,Y_2,...Y_n) = P(Y_i|X,Y_{i-1},Y_{i+1})$$
則稱$P(Y|X)$為線性鏈條件隨機場。
5. 線性鏈條件隨機場的引數化形式
對於上一節講到的linear-CRF,我們如何將其轉化為可以學習的機器學習模型呢?這是通過特徵函式和其權重係數來定義的。什麼是特徵函式呢?
在linear-CRF中,特徵函式分為兩類,第一類是定義在$Y$節點上的節點特徵函式,這類特徵函式只和當前節點有關,記為:$$s_l(y_i, x,i),\;\; l =1,2,...L$$
其中$L$是定義在該節點的節點特徵函式的總個數,$i$是當前節點在序列的位置。
第二類是定義在$Y$上下文的區域性特徵函式,這類特徵函式只和當前節點和上一個節點有關,記為:$$t_k(y_{i-1},y_i, x,i),\;\; k =1,2,...K$$
其中$K$是定義在該節點的區域性特徵函式的總個數,$i$是當前節點在序列的位置。之所以只有上下文相關的區域性特徵函式,沒有不相鄰節點之間的特徵函式,是因為我們的linear-CRF滿足馬爾科夫性。
無論是節點特徵函式還是區域性特徵函式,它們的取值只能是0或者1。即滿足特徵條件或者不滿足特徵條件。同時,我們可以為每個特徵函式賦予一個權值,用以表達我們對這個特徵函式的信任度。假設$t_k$的權重係數是$\lambda_k$,$s_l$的權重係數是$\mu_l$,則linear-CRF由我們所有的$t_k, \lambda_k, s_l, \mu_l$共同決定。
此時我們得到了linear-CRF的引數化形式如下:$$P(y|x) = \frac{1}{Z(x)}exp\Big(\sum\limits_{i,k} \lambda_kt_k(y_{i-1},y_i, x,i) +\sum\limits_{i,l}\mu_ls_l(y_i, x,i)\Big) $$
其中,$Z(x)$為規範化因子:$$Z(x) =\sum\limits_{y} exp\Big(\sum\limits_{i,k} \lambda_kt_k(y_{i-1},y_i, x,i) +\sum\limits_{i,l}\mu_ls_l(y_i, x,i)\Big)$$
回到特徵函式本身,每個特徵函式定義了一個linear-CRF的規則,則其係數定義了這個規則的可信度。所有的規則和其可信度一起構成了我們的linear-CRF的最終的條件概率分佈。
6. 線性鏈條件隨機場例項
這裡我們給出一個linear-CRF用於詞性標註的例項,為了方便,我們簡化了詞性的種類。假設輸入的都是三個詞的句子,即$X=(X_1,X_2,X_3)$,輸出的詞性標記為$Y=(Y_1,Y_2,Y_3)$,其中$Y \in \{1(名詞),2(動詞)\}$
這裡只標記出取值為1的特徵函式如下:$$t_1 =t_1(y_{i-1} = 1, y_i =2,x,i), i =2,3,\;\;\lambda_1=1 $$
$$t_2 =t_2(y_1=1,y_2=1,x,2)\;\;\lambda_2=0.5$$
$$t_3 =t_3(y_2=2,y_3=1,x,3)\;\;\lambda_3=1$$
$$t_4 =t_4(y_1=2,y_2=1,x,2)\;\;\lambda_4=1$$
$$t_5 =t_5(y_2=2,y_3=2,x,3)\;\;\lambda_5=0.2$$
$$s_1 =s_1(y_1=1,x,1)\;\;\mu_1 =1$$
$$s_2 =s_2( y_i =2,x,i), i =1,2,\;\;\mu_2=0.5$$
$$s_3 =s_3( y_i =1,x,i), i =2,3,\;\;\mu_3=0.8$$
$$s_4 =s_4(y_3=2,x,3)\;\;\mu_4 =0.5$$
求標記(1,2,2)的非規範化概率。
利用linear-CRF的引數化公式,我們有:$$P(y|x) \propto exp\Big[\sum\limits_{k=1}^5\lambda_k\sum\limits_{i=2}^3t_k(y_{i-1},y_i, x,i) + \sum\limits_{l=1}^4\mu_l\sum\limits_{i=1}^3s_l(y_i, x,i) \Big]$$
帶入(1,2,2)我們有:$$P(y_1=1,y_2=2,y_3=2|x) \propto exp(3.2)$$
7. 線性鏈條件隨機場的簡化形式
在上幾節裡面,我們用$s_l$表示節點特徵函式,用$t_k$表示區域性特徵函式,同時也用了不同的符號表示權重係數,導致表示起來比較麻煩。其實我們可以對特徵函式稍加整理,將其統一起來。
假設我們在某一節點我們有$K_1$個區域性特徵函式和$K_2$個節點特徵函式,總共有$K=K_1+K_2$個特徵函式。我們用一個特徵函式$f_k(y_{i-1},y_i, x,i)$來統一表示如下:
$$f_k(y_{i-1},y_i, x,i)= \begin{cases} t_k(y_{i-1},y_i, x,i) & {k=1,2,...K_1}\\ s_l(y_i, x,i)& {k=K_1+l,\; l=1,2...,K_2} \end{cases}$$
對$f_k(y_{i-1},y_i, x,i)$在各個序列位置求和得到:$$f_k(y,x) = \sum\limits_{i=1}^nf_k(y_{i-1},y_i, x,i)$$
同時我們也統一$f_k(y_{i-1},y_i, x,i)$對應的權重係數$w_k$如下:
$$w_k= \begin{cases} \lambda_k & {k=1,2,...K_1}\\ \mu_l & {k=K_1+l,\; l=1,2...,K_2} \end{cases}$$
這樣,我們的linear-CRF的引數化形式簡化為:$$P(y|x) = \frac{1}{Z(x)}exp\sum\limits_{k=1}^Kw_kf_k(y,x) $$
其中,$Z(x)$為規範化因子:$$Z(x) =\sum\limits_{y}exp\sum\limits_{k=1}^Kw_kf_k(y,x)$$
如果將上兩式中的$w_k$與$f_k$的用向量表示,即:$$w=(w_1,w_2,...w_K)^T\;\;\; F(y,x) =(f_1(y,x),f_2(y,x),...f_K(y,x))^T$$
則linear-CRF的引數化形式簡化為內積形式如下:$$P_w(y|x) = \frac{exp(w \bullet F(y,x))}{Z_w(x)} = \frac{exp(w \bullet F(y,x))}{\sum\limits_{y}exp(w \bullet F(y,x))}$$
8. 線性鏈條件隨機場的矩陣形式
將上一節統一後的linear-CRF公式加以整理,我們還可以將linear-CRF的引數化形式寫成矩陣形式。為此我們定義一個$m \times m$的矩陣$M$,$m$為$y$所有可能的狀態的取值個數。$M$定義如下:$$M_i(x) = \Big[ M_i(y_{i-1},y_i |x)\Big] = \Big[ exp(W_i(y_{i-1},y_i |x))\Big] = \Big[ exp(\sum\limits_{k=1}^Kw_kf_k(y_{i-1},y_i, x,i))\Big]$$
我們引入起點和終點標記$y_0 =start, y_{n+1} = stop$, 這樣,標記序列$y$的非規範化概率可以通過$n+1$個矩陣元素的乘積得到,即:$$P_w(y|x) = \frac{1}{Z_w(x)}\prod_{i=1}^{n+1}M_i(y_{i-1},y_i |x) $$
其中$Z_w(x)$為規範化因子。
以上就是linear-CRF的模型基礎,後面我們會討論linear-CRF和HMM類似的三個問題的求解方法。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)