在前面我們講到了深度學習的兩類神經網路模型的原理,第一類是前向的神經網路,即DNN和CNN。第二類是有反饋的神經網路,即RNN和LSTM。今天我們就總結下深度學習裡的第三類神經網路模型:玻爾茲曼機。主要關注於這類模型中的受限玻爾茲曼機(Restricted Boltzmann Machine,以下簡稱RBM), RBM模型及其推廣在工業界比如推薦系統中得到了廣泛的應用。
1. RBM模型結構
玻爾茲曼機是一大類的神經網路模型,但是在實際應用中使用最多的則是RBM。RBM本身模型很簡單,只是一個兩層的神經網路,因此嚴格意義上不能算深度學習的範疇。不過深度玻爾茲曼機(Deep Boltzmann Machine,以下簡稱DBM)可以看做是RBM的推廣。理解了RBM再去研究DBM就不難了,因此本文主要關注於RBM。
回到RBM的結構,它是一個個兩層的神經網路,如下圖所示:

上面一層神經元組成隱藏層(hidden layer), 用$h$向量隱藏層神經元的值。下面一層的神經元組成可見層(visible layer),用$v$向量表示可見層神經元的值。隱藏層和可見層之間是全連線的,這點和DNN類似, 隱藏層神經元之間是獨立的,可見層神經元之間也是獨立的。連線權重可以用矩陣$W$表示。和DNN的區別是,RBM不區分前向和反向,可見層的狀態可以作用於隱藏層,而隱藏層的狀態也可以作用於可見層。隱藏層的偏倚係數是向量$b$,而可見層的偏倚係數是向量$a$。
常用的RBM一般是二值的,即不管是隱藏層還是可見層,它們的神經元的取值只為0或者1。本文只討論二值RBM。
總結下RBM模型結構的結構:主要是權重矩陣$W$, 偏倚係數向量$a$和$b$,隱藏層神經元狀態向量$h$和可見層神經元狀態向量$v$。
2. RBM概率分佈
RBM是基於基於能量的概率分佈模型。怎麼理解呢?分兩部分理解,第一部分是能量函式,第二部分是基於能量函式的概率分佈函式。
對於給定的狀態向量$h$和$v$,則RBM當前的能量函式可以表示為:$$E(v,h) = -a^Tv - b^Th - h^TWv $$
有了能量函式,則我們可以定義RBM的狀態為給定$v,h$的概率分佈為:$$P(v,h) = \frac{1}{Z}e^{-E(v,h)}$$
其中$Z$為歸一化因子,類似於softmax中的歸一化因子,表示式為:$$Z = \sum\limits_{v,h}e^{-E(v,h)}$$
有了概率分佈,我們現在來看條件分佈$P(h|v)$:$$ \begin{align} P(h|v) & = \frac{P(h,v)}{P(v)} \\& = \frac{1}{P(v)}\frac{1}{Z}exp\{a^Tv + b^Th + h^TWv\} \\& = \frac{1}{Z'}exp\{b^Th + h^TWv\} \\& = \frac{1}{Z'}exp\{\sum\limits_{j=1}^{n_h}(b_j^Th_j + h_j^TW_{j,:}v)\} \\& = \frac{1}{Z'} \prod\limits_{j=1}^{n_h}exp\{b_j^Th_j + h_j^TW_{j,:}v\} \end{align} $$
其中$Z'$為新的歸一化係數,表示式為:$$\frac{1}{Z'} = \frac{1}{P(v)}\frac{1}{Z}exp\{a^Tv\}$$
同樣的方式,我們也可以求出$P(v|h)$,這裡就不再列出了。
有了條件概率分佈,現在我們來看看RBM的啟用函式,提到神經網路,我們都繞不開啟用函式,但是上面我們並沒有提到。由於使用的是能量概率模型,RBM的基於條件分佈的啟用函式是很容易推匯出來的。我們以$P(h_j=1|v)$為例推導如下。$$ \begin{align} P(h_j =1|v) & = \frac{P(h_j =1|v)}{P(h_j =1|v) + P(h_j =0|v) } \\& = \frac{exp\{b_j + W_{j,:}v\}}{exp\{0\} + exp\{b_j + W_{j,:}v\}} \\& = \frac{1}{1+ exp\{-(b_j + W_{j,:}v)\}}\\& = sigmoid(b_j + W_{j,:}v) \end{align}$$
從上面可以看出, RBM裡從可見層到隱藏層用的其實就是sigmoid啟用函式。同樣的方法,我們也可以得到隱藏層到可見層用的也是sigmoid啟用函式。即:$$ P(v_j =1|h) = sigmoid(a_j + W_{:,j}^Th)$$
有了啟用函式,我們就可以從可見層和引數推匯出隱藏層的神經元的取值概率了。對於0,1取值的情況,則大於0.5即取值為1。從隱藏層和引數推匯出可見的神經元的取值方法也是一樣的。
3. RBM模型的損失函式與優化
RBM模型的關鍵就是求出我們模型中的引數$W,a,b$。如果求出呢?對於訓練集的m個樣本,RBM一般採用對數損失函式,即期望最小化下式:$$L(W,a,b) = -\sum\limits_{i=1}^{m}ln(P(V^{(i)}))$$
對於優化過程,我們是首先想到的當然是梯度下降法來迭代求出$W,a,b$。我們首先來看單個樣本的梯度計算, 單個樣本的損失函式為:$-ln(P(V))$, 我們先看看$-ln(P(V))$具體的內容, :$$ \begin{align} -ln(P(V)) & = -ln(\frac{1}{Z}\sum\limits_he^{-E(V,h)}) \\& = lnZ - ln(\sum\limits_he^{-E(V,h)}) \\& = ln(\sum\limits_{v,h}e^{-E(v,h)}) - ln(\sum\limits_he^{-E(V,h)}) \end{align} $$
注意,這裡面$V$表示的是某個特定訓練樣本,而$v$指的是任意一個樣本。
我們以$a_i$的梯度計算為例:$$\begin{align} \frac{\partial (-ln(P(V)))}{\partial a_i} & = \frac{1}{\partial a_i} \partial{ln(\sum\limits_{v,h}e^{-E(v,h)})} - \frac{1}{\partial a_i} \partial{ln(\sum\limits_he^{-E(V,h)})} \\& = -\frac{1}{\sum\limits_{v,h}e^{-E(v,h)}}\sum\limits_{v,h}e^{-E(v,h)}\frac{\partial E(v,h)}{\partial a_i} + \frac{1}{\sum\limits_{h}e^{-E(V,h)}}\sum\limits_{h}e^{-E(V,h)}\frac{\partial E(V,h)}{\partial a_i} \\& = \sum\limits_{h} P(h|V)\frac{\partial E(V,h)}{\partial a_i} - \sum\limits_{v,h}P(h,v)\frac{\partial E(v,h)}{\partial a_i} \\& = - \sum\limits_{h} P(h|V)V_i + \sum\limits_{v,h}P(h,v)v_i \\& = - \sum\limits_{h} P(h|V)V_i + \sum\limits_{v}P(v)\sum\limits_{h}P(h|v)v_i \\& = \sum\limits_{v}P(v)v_i - V_i \end{align} $$
其中用到了:$$\sum\limits_{h}P(h|v)=1 \;\;\; \sum\limits_{h}P(h|V)=1$$
同樣的方法,可以得到$W,b$的梯度。這裡就不推導了,直接給出結果:$$ \frac{\partial (-ln(P(V)))}{\partial b_i} = \sum\limits_{v}P(v)P(h_i=1|v) - P(h_i=1|V) $$$$ \frac{\partial (-ln(P(V)))}{\partial W_{ij}} = \sum\limits_{v}P(v)P(h_i=1|v)v_j - P(h_i=1|V)V_j $$
雖然梯度下降法可以從理論上解決RBM的優化,但是在實際應用中,由於概率分佈的計算量大,因為概率分佈有$2^{n_v+n_h}$種情況, 所以往往不直接按上面的梯度公式去求所有樣本的梯度和,而是用基於MCMC的方法來模擬計算求解每個樣本的梯度損失再求梯度和,常用的方法是基於Gibbs取樣的對比散度方法來求解,對於對比散度方法,由於需要MCMC的知識,這裡就不展開了。對對比散度方法感興趣的可以看參考文獻中2的《A Practical Guide to Training Restricted Boltzmann Machines》,對於MCMC,後面我專門開篇來講。
4. RBM在實際中應用方法
大家也許會疑惑,這麼一個模型在實際中如何能夠應用呢?比如在推薦系統中是如何應用的呢?這裡概述下推薦系統中使用的常用思路。
RBM可以看做是一個編碼解碼的過程,從可見層到隱藏層就是編碼,而反過來從隱藏層到可見層就是解碼。在推薦系統中,我們可以把每個使用者對各個物品的評分做為可見層神經元的輸入,然後有多少個使用者就有了多少個訓練樣本。由於使用者不是對所有的物品都有評分,所以任意樣本有些可見層神經元沒有值。但是這不影響我們的模型訓練。在訓練模型時,對於每個樣本,我們僅僅用有使用者數值的可見層神經元來訓練模型。
對於可見層輸入的訓練樣本和隨機初始化的$W,a$,我們可以用上面的sigmoid啟用函式得到隱藏層的神經元的0,1值,這就是編碼。然後反過來從隱藏層的神經元值和$W,b$可以得到可見層輸出,這就是解碼。對於每個訓練樣本, 我們期望編碼解碼後的可見層輸出和我們的之前可見層輸入的差距儘量的小,即上面的對數似然損失函式儘可能小。按照這個損失函式,我們通過迭代優化得到$W,a,b$,然後對於某個用於那些沒有評分的物品,我們用解碼的過程可以得到一個預測評分,取最高的若干評分對應物品即可做使用者物品推薦了。
如果大家對RBM在推薦系統的應用具體內容感興趣,可以閱讀參考文獻3中的《Restricted Boltzmann Machines for Collaborative Filtering》
5. RBM推廣到DBM
RBM很容易推廣到深層的RBM,即我們的DBM。推廣的方法就是加入更多的隱藏層,比如一個三層的DBM如下:
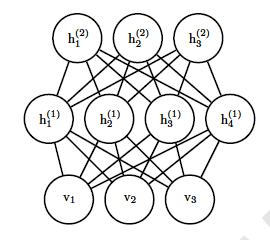
當然隱藏層的層數可以是任意的,隨著層數越來越複雜,那模型怎麼表示呢?其實DBM也可以看做是一個RBM,比如下圖的一個4層DBM,稍微加以變換就可以看做是一個DBM。
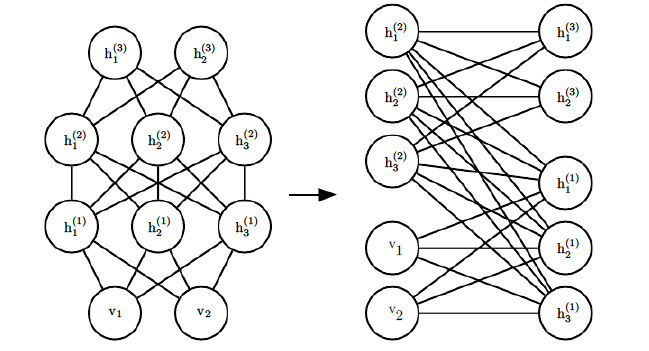
將可見層和偶數隱藏層放在一邊,將奇數隱藏層放在另一邊,我們就得到了RBM,和RBM的細微區別只是現在的RBM並不是全連線的,其實也可以看做部分權重為0的全連線RBM。RBM的演算法思想可以在DBM上使用。只是此時我們的模型引數更加的多,而且迭代求解引數也更加複雜了。
6. RBM小結
RBM所在的玻爾茲曼機流派是深度學習中三大流派之一,也是目前比較熱門的創新區域之一,目前在實際應用中的比較成功的是推薦系統。以後應該會有更多型別的玻爾茲曼機及應用開發出來,讓我們拭目以待吧!
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)
參考資料:
1) Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
2) A Practical Guide to Training Restricted Boltzmann Machines, by G. Hinton
3) Restricted Boltzmann Machines for Collaborative Filtering, by G. Hinton