在K-Means聚類演算法原理中,我們講到了K-Means和Mini Batch K-Means的聚類原理。這裡我們再來看看另外一種常見的聚類演算法BIRCH。BIRCH演算法比較適合於資料量大,類別數K也比較多的情況。它執行速度很快,只需要單遍掃描資料集就能進行聚類,當然需要用到一些技巧,下面我們就對BIRCH演算法做一個總結。
1. BIRCH概述
BIRCH的全稱是利用層次方法的平衡迭代規約和聚類(Balanced Iterative Reducing and Clustering Using Hierarchies),名字實在是太長了,不過沒關係,其實只要明白它是用層次方法來聚類和規約資料就可以了。剛才提到了,BIRCH只需要單遍掃描資料集就能進行聚類,那它是怎麼做到的呢?
BIRCH演算法利用了一個樹結構來幫助我們快速的聚類,這個數結構類似於平衡B+樹,一般將它稱之為聚類特徵樹(Clustering Feature Tree,簡稱CF Tree)。這顆樹的每一個節點是由若干個聚類特徵(Clustering Feature,簡稱CF)組成。從下圖我們可以看看聚類特徵樹是什麼樣子的:每個節點包括葉子節點都有若干個CF,而內部節點的CF有指向孩子節點的指標,所有的葉子節點用一個雙向連結串列連結起來。
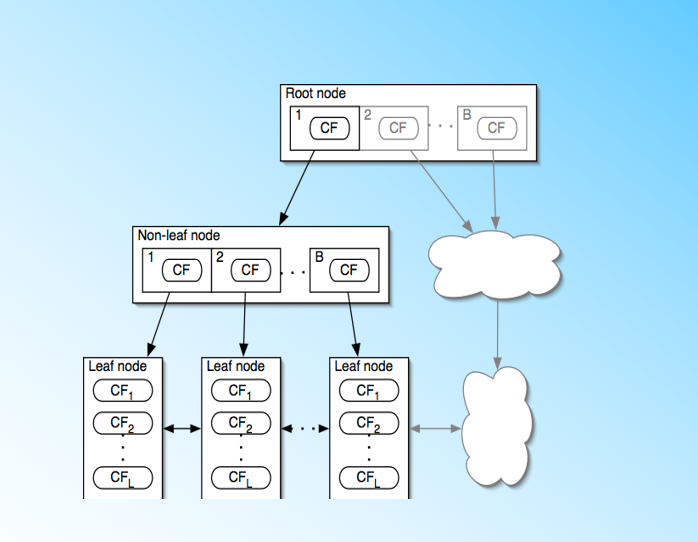
有了聚類特徵樹的概念,我們再對聚類特徵樹和其中節點的聚類特徵CF做進一步的講解。
2. 聚類特徵CF與聚類特徵樹CF Tree
在聚類特徵樹中,一個聚類特徵CF是這樣定義的:每一個CF是一個三元組,可以用(N,LS,SS)表示。其中N代表了這個CF中擁有的樣本點的數量,這個好理解;LS代表了這個CF中擁有的樣本點各特徵維度的和向量,SS代表了這個CF中擁有的樣本點各特徵維度的平方和。舉個例子如下圖,在CF Tree中的某一個節點的某一個CF中,有下面5個樣本(3,4), (2,6), (4,5), (4,7), (3,8)。則它對應的N=5, LS=$(3+2+4+4+3, 4+6+5+7+8) = (16,30)$, SS =$(3^2+2^2+4^2 +4^2+3^2 + 4^2+6^2+5^2 +7^2+8^2) = (54 + 190) = 244$
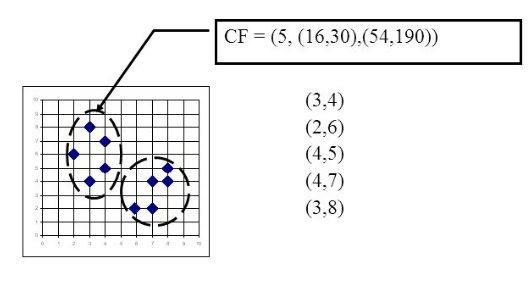
CF有一個很好的性質,就是滿足線性關係,也就是$CF1+CF2 = (N_1+N_2, LS_1+LS_2, SS_1 +SS_2)$。這個性質從定義也很好理解。如果把這個性質放在CF Tree上,也就是說,在CF Tree中,對於每個父節點中的CF節點,它的(N,LS,SS)三元組的值等於這個CF節點所指向的所有子節點的三元組之和。如下圖所示:
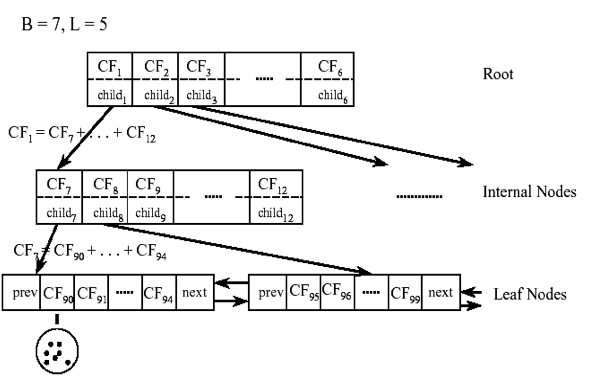
從上圖中可以看出,根節點的CF1的三元組的值,可以從它指向的6個子節點(CF7 - CF12)的值相加得到。這樣我們在更新CF Tree的時候,可以很高效。
對於CF Tree,我們一般有幾個重要引數,第一個引數是每個內部節點的最大CF數B,第二個引數是每個葉子節點的最大CF數L,第三個引數是針對葉子節點中某個CF中的樣本點來說的,它是葉節點每個CF的最大樣本半徑閾值T,也就是說,在這個CF中的所有樣本點一定要在半徑小於T的一個超球體內。對於上圖中的CF Tree,限定了B=7, L=5, 也就是說內部節點最多有7個CF,而葉子節點最多有5個CF。
3. 聚類特徵樹CF Tree的生成
下面我們看看怎麼生成CF Tree。我們先定義好CF Tree的引數: 即內部節點的最大CF數B, 葉子節點的最大CF數L, 葉節點每個CF的最大樣本半徑閾值T
在最開始的時候,CF Tree是空的,沒有任何樣本,我們從訓練集讀入第一個樣本點,將它放入一個新的CF三元組A,這個三元組的N=1,將這個新的CF放入根節點,此時的CF Tree如下圖:
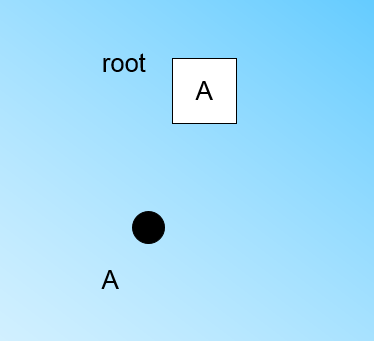
現在我們繼續讀入第二個樣本點,我們發現這個樣本點和第一個樣本點A,在半徑為T的超球體範圍內,也就是說,他們屬於一個CF,我們將第二個點也加入CF A,此時需要更新A的三元組的值。此時A的三元組中N=2。此時的CF Tree如下圖:
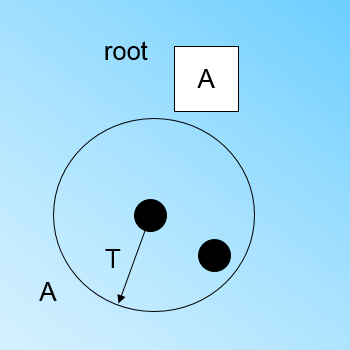
此時來了第三個節點,結果我們發現這個節點不能融入剛才前面的節點形成的超球體內,也就是說,我們需要一個新的CF三元組B,來容納這個新的值。此時根節點有兩個CF三元組A和B,此時的CF Tree如下圖:
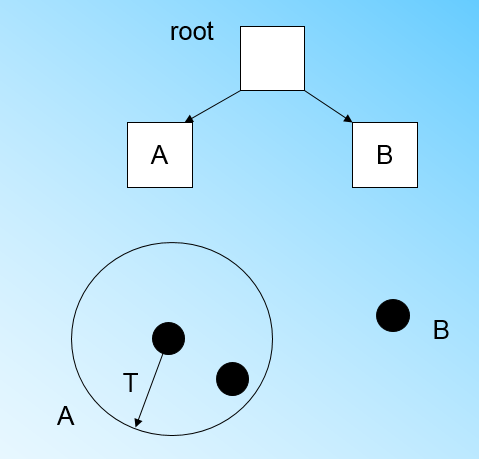
當來到第四個樣本點的時候,我們發現和B在半徑小於T的超球體,這樣更新後的CF Tree如下圖:
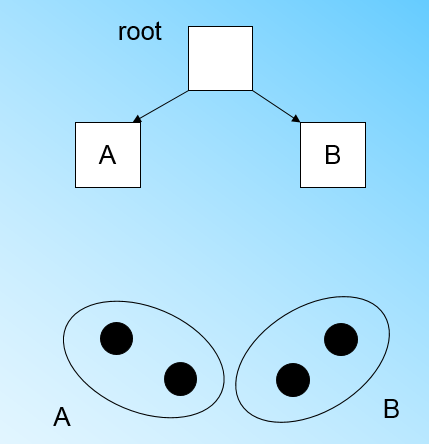
那個什麼時候CF Tree的節點需要分裂呢?假設我們現在的CF Tree 如下圖, 葉子節點LN1有三個CF, LN2和LN3各有兩個CF。我們的葉子節點的最大CF數L=3。此時一個新的樣本點來了,我們發現它離LN1節點最近,因此開始判斷它是否在sc1,sc2,sc3這3個CF對應的超球體之內,但是很不幸,它不在,因此它需要建立一個新的CF,即sc8來容納它。問題是我們的L=3,也就是說LN1的CF個數已經達到最大值了,不能再建立新的CF了,怎麼辦?此時就要將LN1葉子節點一分為二了。
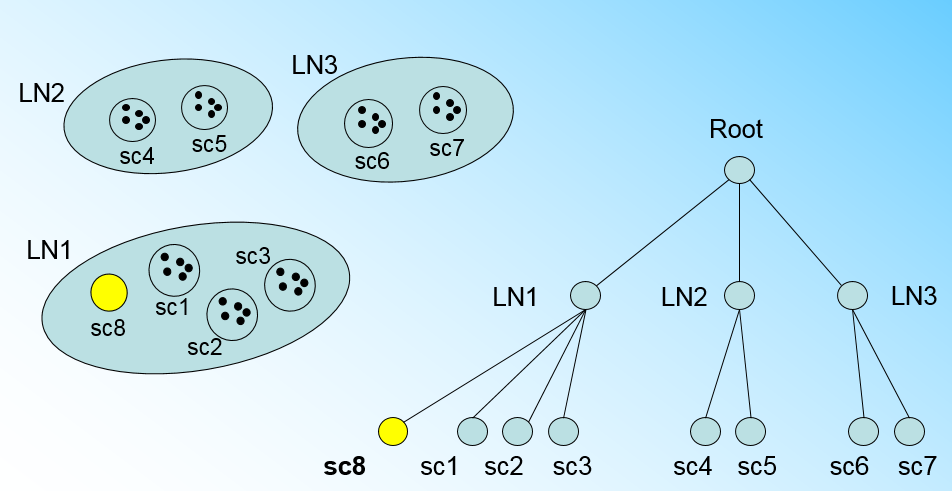
我們將LN1裡所有CF元組中,找到兩個最遠的CF做這兩個新葉子節點的種子CF,然後將LN1節點裡所有CF sc1, sc2, sc3,以及新樣本點的新元組sc8劃分到兩個新的葉子節點上。將LN1節點劃分後的CF Tree如下圖:
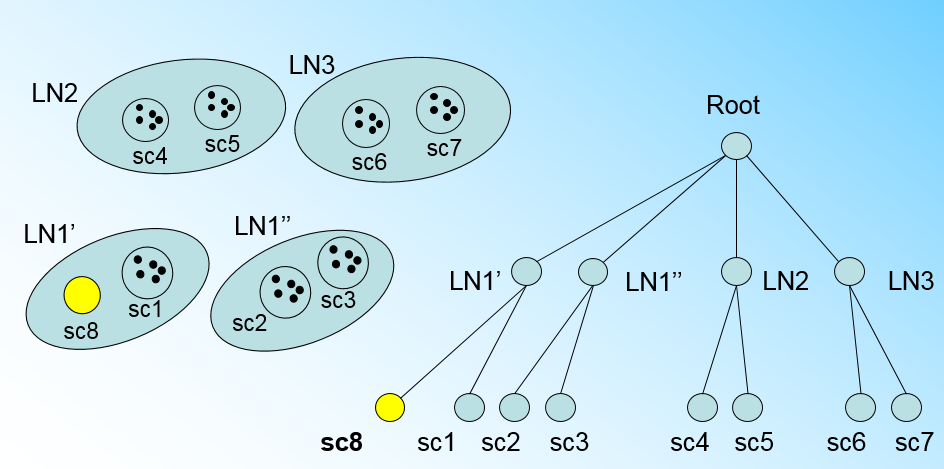
如果我們的內部節點的最大CF數B=3,則此時葉子節點一分為二會導致根節點的最大CF數超了,也就是說,我們的根節點現在也要分裂,分裂的方法和葉子節點分裂一樣,分裂後的CF Tree如下圖:
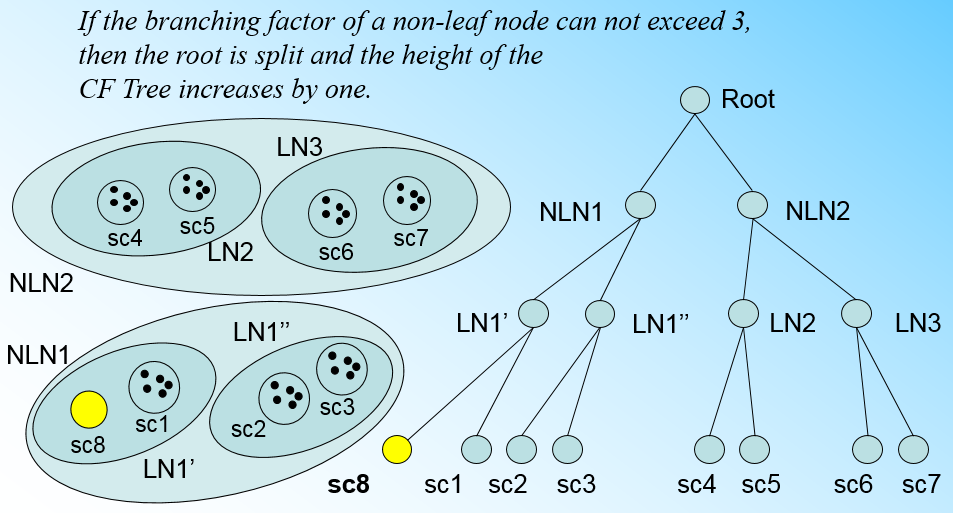
有了上面這一系列的圖,相信大家對於CF Tree的插入就沒有什麼問題了,總結下CF Tree的插入:
1. 從根節點向下尋找和新樣本距離最近的葉子節點和葉子節點裡最近的CF節點
2. 如果新樣本加入後,這個CF節點對應的超球體半徑仍然滿足小於閾值T,則更新路徑上所有的CF三元組,插入結束。否則轉入3.
3. 如果當前葉子節點的CF節點個數小於閾值L,則建立一個新的CF節點,放入新樣本,將新的CF節點放入這個葉子節點,更新路徑上所有的CF三元組,插入結束。否則轉入4。
4.將當前葉子節點劃分為兩個新葉子節點,選擇舊葉子節點中所有CF元組裡超球體距離最遠的兩個CF元組,分佈作為兩個新葉子節點的第一個CF節點。將其他元組和新樣本元組按照距離遠近原則放入對應的葉子節點。依次向上檢查父節點是否也要分裂,如果需要按和葉子節點分裂方式相同。
4. BIRCH演算法
上面講了半天的CF Tree,終於我們可以步入正題BIRCH演算法,其實將所有的訓練集樣本建立了CF Tree,一個基本的BIRCH演算法就完成了,對應的輸出就是若干個CF節點,每個節點裡的樣本點就是一個聚類的簇。也就是說BIRCH演算法的主要過程,就是建立CF Tree的過程。
當然,真實的BIRCH演算法除了建立CF Tree來聚類,其實還有一些可選的演算法步驟的,現在我們就來看看 BIRCH演算法的流程。
1) 將所有的樣本依次讀入,在記憶體中建立一顆CF Tree, 建立的方法參考上一節。
2)(可選)將第一步建立的CF Tree進行篩選,去除一些異常CF節點,這些節點一般裡面的樣本點很少。對於一些超球體距離非常近的元組進行合併
3)(可選)利用其它的一些聚類演算法比如K-Means對所有的CF元組進行聚類,得到一顆比較好的CF Tree.這一步的主要目的是消除由於樣本讀入順序導致的不合理的樹結構,以及一些由於節點CF個數限制導致的樹結構分裂。
4)(可選)利用第三步生成的CF Tree的所有CF節點的質心,作為初始質心點,對所有的樣本點按距離遠近進行聚類。這樣進一步減少了由於CF Tree的一些限制導致的聚類不合理的情況。
從上面可以看出,BIRCH演算法的關鍵就是步驟1,也就是CF Tree的生成,其他步驟都是為了優化最後的聚類結果。
5. BIRCH演算法小結
BIRCH演算法可以不用輸入類別數K值,這點和K-Means,Mini Batch K-Means不同。如果不輸入K值,則最後的CF元組的組數即為最終的K,否則會按照輸入的K值對CF元組按距離大小進行合併。
一般來說,BIRCH演算法適用於樣本量較大的情況,這點和Mini Batch K-Means類似,但是BIRCH適用於類別數比較大的情況,而Mini Batch K-Means一般用於類別數適中或者較少的時候。BIRCH除了聚類還可以額外做一些異常點檢測和資料初步按類別規約的預處理。但是如果資料特徵的維度非常大,比如大於20,則BIRCH不太適合,此時Mini Batch K-Means的表現較好。
對於調參,BIRCH要比K-Means,Mini Batch K-Means複雜,因為它需要對CF Tree的幾個關鍵的引數進行調參,這幾個引數對CF Tree的最終形式影響很大。
最後總結下BIRCH演算法的優缺點:
BIRCH演算法的主要優點有:
1) 節約記憶體,所有的樣本都在磁碟上,CF Tree僅僅存了CF節點和對應的指標。
2) 聚類速度快,只需要一遍掃描訓練集就可以建立CF Tree,CF Tree的增刪改都很快。
3) 可以識別噪音點,還可以對資料集進行初步分類的預處理
BIRCH演算法的主要缺點有:
1) 由於CF Tree對每個節點的CF個數有限制,導致聚類的結果可能和真實的類別分佈不同.
2) 對高維特徵的資料聚類效果不好。此時可以選擇Mini Batch K-Means
3) 如果資料集的分佈簇不是類似於超球體,或者說不是凸的,則聚類效果不好。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)