K近鄰法(k-nearest neighbors,KNN)是一種很基本的機器學習方法了,在我們平常的生活中也會不自主的應用。比如,我們判斷一個人的人品,只需要觀察他來往最密切的幾個人的人品好壞就可以得出了。這裡就運用了KNN的思想。KNN方法既可以做分類,也可以做迴歸,這點和決策樹演算法相同。
KNN做迴歸和分類的主要區別在於最後做預測時候的決策方式不同。KNN做分類預測時,一般是選擇多數表決法,即訓練集裡和預測的樣本特徵最近的K個樣本,預測為裡面有最多類別數的類別。而KNN做迴歸時,一般是選擇平均法,即最近的K個樣本的樣本輸出的平均值作為迴歸預測值。由於兩者區別不大,雖然本文主要是講解KNN的分類方法,但思想對KNN的迴歸方法也適用。由於scikit-learn裡只使用了蠻力實現(brute-force),KD樹實現(KDTree)和球樹(BallTree)實現,本文只討論這幾種演算法的實現原理。其餘的實現方法比如BBF樹,MVP樹等,在這裡不做討論。
1. KNN演算法三要素
KNN演算法我們主要要考慮三個重要的要素,對於固定的訓練集,只要這三點確定了,演算法的預測方式也就決定了。這三個最終的要素是k值的選取,距離度量的方式和分類決策規則。
對於分類決策規則,一般都是使用前面提到的多數表決法。所以我們重點是關注與k值的選擇和距離的度量方式。
對於k值的選擇,沒有一個固定的經驗,一般根據樣本的分佈,選擇一個較小的值,可以通過交叉驗證選擇一個合適的k值。
選擇較小的k值,就相當於用較小的領域中的訓練例項進行預測,訓練誤差會減小,只有與輸入例項較近或相似的訓練例項才會對預測結果起作用,與此同時帶來的問題是泛化誤差會增大,換句話說,K值的減小就意味著整體模型變得複雜,容易發生過擬合;
選擇較大的k值,就相當於用較大領域中的訓練例項進行預測,其優點是可以減少泛化誤差,但缺點是訓練誤差會增大。這時候,與輸入例項較遠(不相似的)訓練例項也會對預測器作用,使預測發生錯誤,且K值的增大就意味著整體的模型變得簡單。
一個極端是k等於樣本數m,則完全沒有分類,此時無論輸入例項是什麼,都只是簡單的預測它屬於在訓練例項中最多的類,模型過於簡單。
對於距離的度量,我們有很多的距離度量方式,但是最常用的是歐式距離,即對於兩個n維向量x和y,兩者的歐式距離定義為:$$D(x,y) = \sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + ... + (x_n-y_n)^2} = \sqrt{\sum\limits_{i=1}^{n}(x_i-y_i)^2} $$
大多數情況下,歐式距離可以滿足我們的需求,我們不需要再去操心距離的度量。
當然我們也可以用他的距離度量方式。比如曼哈頓距離,定義為:$$D(x,y) =|x_1-y_1| + |x_2-y_2| + ... + |x_n-y_n| =\sum\limits_{i=1}^{n}|x_i-y_i| $$
更加通用點,比如閔可夫斯基距離(Minkowski Distance),定義為:$$D(x,y) =\sqrt[p]{(|x_1-y_1|)^p + (|x_2-y_2|)^p + ... + (|x_n-y_n|)^p} =\sqrt[p]{\sum\limits_{i=1}^{n}(|x_i-y_i|)^p} $$
可以看出,歐式距離是閔可夫斯基距離距離在p=2時的特例,而曼哈頓距離是p=1時的特例。
2. KNN演算法蠻力實現
從本節起,我們開始討論KNN演算法的實現方式。首先我們看看最想當然的方式。
既然我們要找到k個最近的鄰居來做預測,那麼我們只需要計算預測樣本和所有訓練集中的樣本的距離,然後計算出最小的k個距離即可,接著多數表決,很容易做出預測。這個方法的確簡單直接,在樣本量少,樣本特徵少的時候有效。但是在實際運用中很多時候用不上,為什麼呢?因為我們經常碰到樣本的特徵數有上千以上,樣本量有幾十萬以上,如果我們這要去預測少量的測試集樣本,演算法的時間效率很成問題。因此,這個方法我們一般稱之為蠻力實現。比較適合於少量樣本的簡單模型的時候用。
既然蠻力實現在特徵多,樣本多的時候很有侷限性,那麼我們有沒有其他的好辦法呢?有!這裡我們講解兩種辦法,一個是KD樹實現,一個是球樹實現。
3. KNN演算法之KD樹實現原理
KD樹演算法沒有一開始就嘗試對測試樣本分類,而是先對訓練集建模,建立的模型就是KD樹,建好了模型再對測試集做預測。所謂的KD樹就是K個特徵維度的樹,注意這裡的K和KNN中的K的意思不同。KNN中的K代表最近的K個樣本,KD樹中的K代表樣本特徵的維數。為了防止混淆,後面我們稱特徵維數為n。
KD樹演算法包括三步,第一步是建樹,第二部是搜尋最近鄰,最後一步是預測。
3.1 KD樹的建立
我們首先來看建樹的方法。KD樹建樹採用的是從m個樣本的n維特徵中,分別計算n個特徵的取值的方差,用方差最大的第k維特徵$n_k$來作為根節點。對於這個特徵,我們選擇特徵$n_k$的取值的中位數$n_{kv}$對應的樣本作為劃分點,對於所有第k維特徵的取值小於$n_{kv}$的樣本,我們劃入左子樹,對於第k維特徵的取值大於等於$n_{kv}$的樣本,我們劃入右子樹,對於左子樹和右子樹,我們採用和剛才同樣的辦法來找方差最大的特徵來做更節點,遞迴的生成KD樹。
具體流程如下圖:
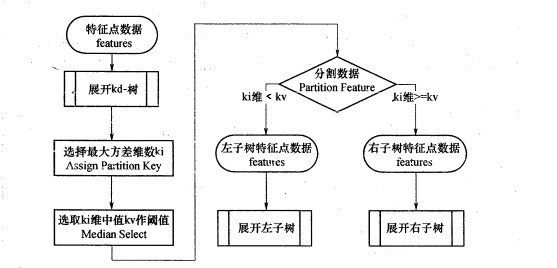
比如我們有二維樣本6個,{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},構建kd樹的具體步驟為:
1)找到劃分的特徵。6個資料點在x,y維度上的資料方差分別為6.97,5.37,所以在x軸上方差更大,用第1維特徵建樹。
2)確定劃分點(7,2)。根據x維上的值將資料排序,6個資料的中值(所謂中值,即中間大小的值)為7,所以劃分點的資料是(7,2)。這樣,該節點的分割超平面就是通過(7,2)並垂直於:劃分點維度的直線x=7;
3)確定左子空間和右子空間。 分割超平面x=7將整個空間分為兩部分:x<=7的部分為左子空間,包含3個節點={(2,3),(5,4),(4,7)};另一部分為右子空間,包含2個節點={(9,6),(8,1)}。
4)用同樣的辦法劃分左子樹的節點{(2,3),(5,4),(4,7)}和右子樹的節點{(9,6),(8,1)}。最終得到KD樹。
最後得到的KD樹如下:
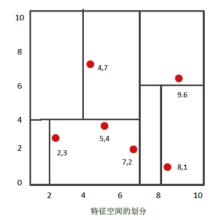
3.2 KD樹搜尋最近鄰
當我們生成KD樹以後,就可以去預測測試集裡面的樣本目標點了。對於一個目標點,我們首先在KD樹裡面找到包含目標點的葉子節點。以目標點為圓心,以目標點到葉子節點樣本例項的距離為半徑,得到一個超球體,最近鄰的點一定在這個超球體內部。然後返回葉子節點的父節點,檢查另一個子節點包含的超矩形體是否和超球體相交,如果相交就到這個子節點尋找是否有更加近的近鄰,有的話就更新最近鄰。如果不相交那就簡單了,我們直接返回父節點的父節點,在另一個子樹繼續搜尋最近鄰。當回溯到根節點時,演算法結束,此時儲存的最近鄰節點就是最終的最近鄰。
從上面的描述可以看出,KD樹劃分後可以大大減少無效的最近鄰搜尋,很多樣本點由於所在的超矩形體和超球體不相交,根本不需要計算距離。大大節省了計算時間。
我們用3.1建立的KD樹,來看對點(2,4.5)找最近鄰的過程。
先進行二叉查詢,先從(7,2)查詢到(5,4)節點,在進行查詢時是由y = 4為分割超平面的,由於查詢點為y值為4.5,因此進入右子空間查詢到(4,7),形成搜尋路徑<(7,2),(5,4),(4,7)>,但 (4,7)與目標查詢點的距離為3.202,而(5,4)與查詢點之間的距離為3.041,所以(5,4)為查詢點的最近點; 以(2,4.5)為圓心,以3.041為半徑作圓,如下圖所示。可見該圓和y = 4超平面交割,所以需要進入(5,4)左子空間進行查詢,也就是將(2,3)節點加入搜尋路徑中得<(7,2),(2,3)>;於是接著搜尋至(2,3)葉子節點,(2,3)距離(2,4.5)比(5,4)要近,所以最近鄰點更新為(2,3),最近距離更新為1.5;回溯查詢至(5,4),直到最後回溯到根結點(7,2)的時候,以(2,4.5)為圓心1.5為半徑作圓,並不和x = 7分割超平面交割,如下圖所示。至此,搜尋路徑回溯完,返回最近鄰點(2,3),最近距離1.5。
對應的圖如下:
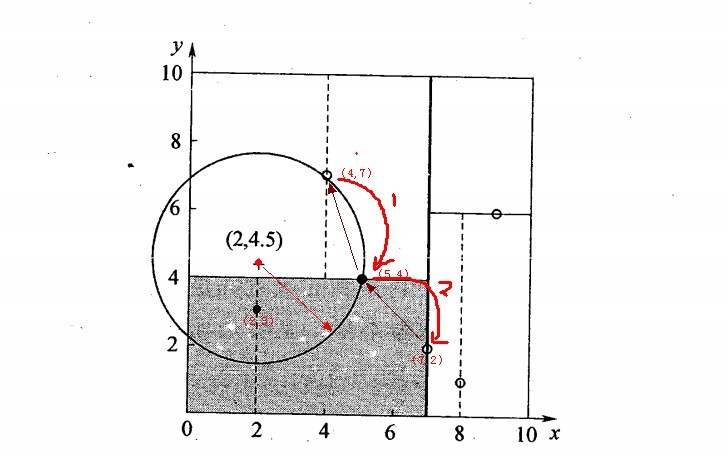
3.3 KD樹預測
有了KD樹搜尋最近鄰的辦法,KD樹的預測就很簡單了,在KD樹搜尋最近鄰的基礎上,我們選擇到了第一個最近鄰樣本,就把它置為已選。在第二輪中,我們忽略置為已選的樣本,重新選擇最近鄰,這樣跑k次,就得到了目標的K個最近鄰,然後根據多數表決法,如果是KNN分類,預測為K個最近鄰里面有最多類別數的類別。如果是KNN迴歸,用K個最近鄰樣本輸出的平均值作為迴歸預測值。
4. KNN演算法之球樹實現原理
KD樹演算法雖然提高了KNN搜尋的效率,但是在某些時候效率並不高,比如當處理不均勻分佈的資料集時,不管是近似方形,還是矩形,甚至正方形,都不是最好的使用形狀,因為他們都有角。一個例子如下圖:

如果黑色的例項點離目標點星點再遠一點,那麼虛線圓會如紅線所示那樣擴大,導致與左上方矩形的右下角相交,既然相 交了,那麼就要檢查這個左上方矩形,而實際上,最近的點離星點的距離很近,檢查左上方矩形區域已是多餘。於此我們看見,KD樹把二維平面劃分成一個一個矩形,但矩形區域的角卻是個難以處理的問題。
為了優化超矩形體導致的搜尋效率的問題,牛人們引入了球樹,這種結構可以優化上面的這種問題。
我們現在來看看球樹建樹和搜尋最近鄰的演算法。
4.1 球樹的建立
球樹,顧名思義,就是每個分割塊都是超球體,而不是KD樹裡面的超矩形體。
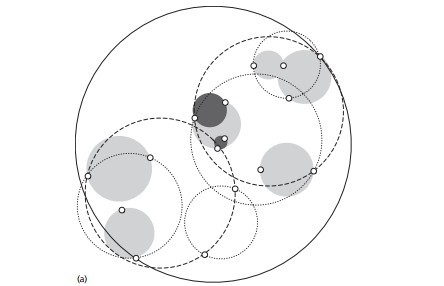
我們看看具體的建樹流程:
1) 先構建一個超球體,這個超球體是可以包含所有樣本的最小球體。
2) 從球中選擇一個離球的中心最遠的點,然後選擇第二個點離第一個點最遠,將球中所有的點分配到離這兩個聚類中心最近的一個上,然後計算每個聚類的中心,以及聚類能夠包含它所有資料點所需的最小半徑。這樣我們得到了兩個子超球體,和KD樹裡面的左右子樹對應。
3)對於這兩個子超球體,遞迴執行步驟2). 最終得到了一個球樹。
可以看出KD樹和球樹類似,主要區別在於球樹得到的是節點樣本組成的最小超球體,而KD得到的是節點樣本組成的超矩形體,這個超球體要與對應的KD樹的超矩形體小,這樣在做最近鄰搜尋的時候,可以避免一些無謂的搜尋。
4.2 球樹搜尋最近鄰
使用球樹找出給定目標點的最近鄰方法是首先自上而下貫穿整棵樹找出包含目標點所在的葉子,並在這個球裡找出與目標點最鄰近的點,這將確定出目標點距離它的最近鄰點的一個上限值,然後跟KD樹查詢一樣,檢查兄弟結點,如果目標點到兄弟結點中心的距離超過兄弟結點的半徑與當前的上限值之和,那麼兄弟結點裡不可能存在一個更近的點;否則的話,必須進一步檢查位於兄弟結點以下的子樹。
檢查完兄弟節點後,我們向父節點回溯,繼續搜尋最小鄰近值。當回溯到根節點時,此時的最小鄰近值就是最終的搜尋結果。
從上面的描述可以看出,KD樹在搜尋路徑優化時使用的是兩點之間的距離來判斷,而球樹使用的是兩邊之和大於第三邊來判斷,相對來說球樹的判斷更加複雜,但是卻避免了更多的搜尋,這是一個權衡。
5. KNN演算法的擴充套件
這裡我們再討論下KNN演算法的擴充套件,限定半徑最近鄰演算法。
有時候我們會遇到這樣的問題,即樣本中某系類別的樣本非常的少,甚至少於K,這導致稀有類別樣本在找K個最近鄰的時候,會把距離其實較遠的其他樣本考慮進來,而導致預測不準確。為了解決這個問題,我們限定最近鄰的一個最大距離,也就是說,我們只在一個距離範圍內搜尋所有的最近鄰,這避免了上述問題。這個距離我們一般稱為限定半徑。
接著我們再討論下另一種擴充套件,最近質心演算法。這個演算法比KNN還簡單。它首先把樣本按輸出類別歸類。對於第 L類的$C_l$個樣本。它會對這$C_l$個樣本的n維特徵中每一維特徵求平均值,最終該類別所有維度的n個平均值形成所謂的質心點。對於樣本中的所有出現的類別,每個類別會最終得到一個質心點。當我們做預測時,僅僅需要比較預測樣本和這些質心的距離,最小的距離對於的質心類別即為預測的類別。這個演算法通常用在文字分類處理上。
6. KNN演算法小結
KNN演算法是很基本的機器學習演算法了,它非常容易學習,在維度很高的時候也有很好的分類效率,因此運用也很廣泛,這裡總結下KNN的優缺點。
KNN的主要優點有:
1) 理論成熟,思想簡單,既可以用來做分類也可以用來做迴歸
2) 可用於非線性分類
3) 訓練時間複雜度比支援向量機之類的演算法低,僅為O(n)
4) 和樸素貝葉斯之類的演算法比,對資料沒有假設,準確度高,對異常點不敏感
KNN的主要缺點有:
1)計算量大,尤其是特徵數非常多的時候
2)樣本不平衡的時候,對稀有類別的預測準確率低
3)KD樹,球樹之類的模型建立需要大量的記憶體
4)使用懶散學習方法,基本上不學習,導致預測時速度比起邏輯迴歸之類的演算法慢
以上就是KNN演算法原理的一個總結,希望可以幫到朋友們,尤其是在用scikit-learn學習KNN的朋友們。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)