前面的文章對線性迴歸做了一個小結,文章在這: 線性迴歸原理小結。裡面對執行緒迴歸的正則化也做了一個初步的介紹。提到了執行緒迴歸的L2正則化-Ridge迴歸,以及執行緒迴歸的L1正則化-Lasso迴歸。但是對於Lasso迴歸的解法沒有提及,本文是對該文的補充和擴充套件。以下都用矩陣法表示,如果對於矩陣分析不熟悉,推薦學習張賢達的《矩陣分析與應用》。
1. 回顧線性迴歸
首先我們簡要回歸下線性迴歸的一般形式:
\(h_\mathbf{\theta}(\mathbf{X}) = \mathbf{X\theta}\)
需要極小化的損失函式是:
\(J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y})\)
如果用梯度下降法求解,則每一輪\(\theta\)迭代的表示式是:
\(\mathbf\theta= \mathbf\theta - \alpha\mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y})\)
其中\(\alpha\)為步長。
如果用最小二乘法,則\(\theta\)的結果是:
\( \mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y} \)
2. 回顧Ridge迴歸
由於直接套用線性迴歸可能產生過擬合,我們需要加入正則化項,如果加入的是L2正則化項,就是Ridge迴歸,有時也翻譯為脊迴歸。它和一般線性迴歸的區別是在損失函式上增加了一個L2正則化的項,和一個調節線性迴歸項和正則化項權重的係數\(\alpha\)。損失函式表示式如下:
\(J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \frac{1}{2}\alpha||\theta||_2^2\)
其中\(\alpha\)為常數係數,需要進行調優。\(||\theta||_2\)為L2範數。
Ridge迴歸的解法和一般線性迴歸大同小異。如果採用梯度下降法,則每一輪\(\theta\)迭代的表示式是:
\(\mathbf\theta= \mathbf\theta - (\beta\mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha\theta)\)
其中\(\beta\)為步長。
如果用最小二乘法,則\(\theta\)的結果是:
\(\mathbf{\theta = (X^TX + \alpha E)^{-1}X^TY}\)
其中E為單位矩陣。
模型變數多的缺點呢?有,這就是下面說的Lasso迴歸。
3. 初識Lasso迴歸
Lasso迴歸有時也叫做線性迴歸的L1正則化,和Ridge迴歸的主要區別就是在正則化項,Ridge迴歸用的是L2正則化,而Lasso迴歸用的是L1正則化。Lasso迴歸的損失函式表示式如下:
\(J(\mathbf\theta) = \frac{1}{2n}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha||\theta||_1\)
其中n為樣本個數,\(\alpha\)為常數係數,需要進行調優。\(||\theta||_1\)為L1範數。
4. 用座標軸下降法求解Lasso迴歸
座標軸下降法顧名思義,是沿著座標軸的方向去下降,這和梯度下降不同。梯度下降是沿著梯度的負方向下降。不過梯度下降和座標軸下降的共性就都是迭代法,通過啟發式的方式一步步迭代求解函式的最小值。
座標軸下降法的數學依據主要是這個結論(此處不做證明):一個可微的凸函式\(J(\theta)\), 其中\(\theta\)是nx1的向量,即有n個維度。如果在某一點\(\overline\theta\),使得\(J(\theta)\)在每一個座標軸\(\overline\theta_i\)(i = 1,2,...n)上都是最小值,那麼\(J(\overline\theta_i)\)就是一個全域性的最小值。
於是我們的優化目標就是在\(\theta\)的n個座標軸上(或者說向量的方向上)對損失函式做迭代的下降,當所有的座標軸上的\(\theta_i\)(i = 1,2,...n)都達到收斂時,我們的損失函式最小,此時的\(\theta\)即為我們要求的結果。
下面我們看看具體的演算法過程:
1. 首先,我們把\(\theta\)向量隨機取一個初值。記為\(\theta^{(0)}\) ,上面的括號裡面的數字代表我們迭代的輪數,當前初始輪數為0.
2. 對於第k輪的迭代。我們從\(\theta_1^{(k)}\)開始,到\(\theta_n^{(k)}\)為止,依次求\(\theta_i^{(k)}\)。\(\theta_i^{(k)}\)的表示式如下:
\( \theta_i^{(k)} \in \underbrace{argmin}_{\theta_i} J(\theta_1^{(k)}, \theta_2^{(k)}, ... \theta_{i-1}^{(k)}, \theta_i, \theta_{i+1}^{(k-1)}, ..., \theta_n^{(k-1)})\)
也就是說\( \theta_i^{(k)} \)是使\(J(\theta_1^{(k)}, \theta_2^{(k)}, ... \theta_{i-1}^{(k)}, \theta_i, \theta_{i+1}^{(k-1)}, ..., \theta_n^{(k-1)})\)最小化時候的\(\theta_i\)的值。此時\(J(\theta)\)只有\( \theta_i^{(k)} \)是變數,其餘均為常量,因此最小值容易通過求導求得。
如果上面這個式子不好理解,我們具體一點,在第k輪,\(\theta\)向量的n個維度的迭代式如下:
\( \theta_1^{(k)} \in \underbrace{argmin}_{\theta_1} J(\theta_1, \theta_2^{(k-1)}, ... , \theta_n^{(k-1)})\)
\( \theta_2^{(k)} \in \underbrace{argmin}_{\theta_2} J(\theta_1^{(k)}, \theta_2, \theta_3^{(k-1)}... , \theta_n^{(k-1)})\)
...
\( \theta_n^{(k)} \in \underbrace{argmin}_{\theta_n} J(\theta_1^{(k)}, \theta_2^{(k)}, ... , \theta_{n-1}^{(k)}, \theta_n)\)
3. 檢查\(\theta^{(k)}\)向量和\(\theta^{(k-1)}\)向量在各個維度上的變化情況,如果在所有維度上變化都足夠小,那麼\(\theta^{(k)}\)即為最終結果,否則轉入2,繼續第k+1輪的迭代。
以上就是座標軸下降法的求極值過程,可以和梯度下降做一個比較:
5. 用最小角迴歸法求解Lasso迴歸
第四節介紹了座標軸下降法求解Lasso迴歸的方法,此處再介紹另一種常用方法, 最小角迴歸法(Least Angle Regression, LARS)。
在介紹最小角迴歸前,我們先看看兩個預備演算法,好吧,這個演算法真沒有那麼好講。
5.1 前向選擇(Forward Selection)演算法
第一個預備演算法是前向選擇(Forward Selection)演算法。
前向選擇演算法的原理是是一種典型的貪心演算法。要解決的問題是對於:
\(\mathbf{Y = X\theta}\)這樣的線性關係,如何求解係數向量\(\mathbf{\theta}\)的問題。其中\(\mathbf{Y}\)為 mx1的向量,\(\mathbf{X}\)為mxn的矩陣,\(\mathbf{\theta}\)為nx1的向量。m為樣本數量,n為特徵維度。
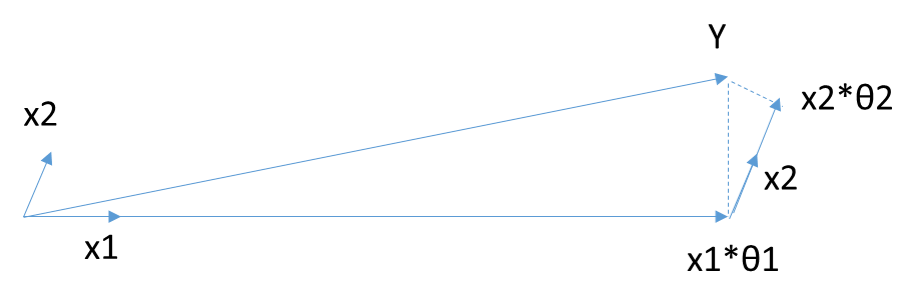
把 矩陣\(\mathbf{X}\)看做n個mx1的向量\(\mathbf{X_i}\)(i=1,2,...n),在\(\mathbf{Y}\)的\(\mathbf{X}\)變數\(\mathbf{X_i}\)(i =1,2,...m)中,選擇和目標\(\mathbf{Y}\)最為接近(餘弦距離最大)的一個變數\(\mathbf{X_k}\),用\(\mathbf{X_k}\)來逼近\(\mathbf{Y}\),得到下式:
\(\overline{\mathbf{Y}} = \mathbf{X_k\theta_k}\)
5.2 前向梯度(Forward Stagewise)演算法
第二個預備演算法是前向梯度(Forward Stagewise)演算法。
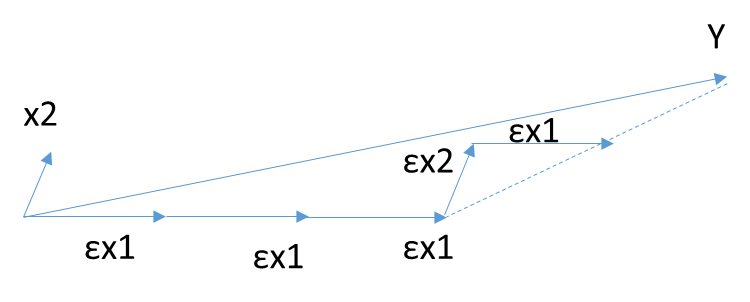
前向梯度演算法和前向選擇演算法有類似的地方,也是在\(\mathbf{Y}\)的\(\mathbf{X}\)變數\(\mathbf{X_i}\)(i =1,2,...n)中,選擇和目標\(\mathbf{Y}\)最為接近(餘弦距離最大)的一個變數\(\mathbf{X_k}\),用\(\mathbf{X_k}\)來逼近\(\mathbf{Y}\),但是前向梯度演算法不是粗暴的用投影,而是每次在最為接近的自變數\(\mathbf{X_t}\)的方向移動一小步,然後再看殘差\(\mathbf{Y_{yes}}\)和哪個\(\mathbf{X_i}\)(i =1,2,...n)最為接近。此時我們也不會把\(\mathbf{X_t}\) 去除,因為我們只是前進了一小步,有可能下面最接近的自變數還是\(\mathbf{X_t}\)。如此進行下去,直到殘差\(\mathbf{Y_{yes}} \)減小到足夠小,演算法停止。
有沒有折中的辦法可以綜合前向梯度演算法和前向選擇演算法的優點,做一個折中呢?有!這就是終於要出場的最小角迴歸法。
5.3 最小角迴歸(Least Angle Regression, LARS)演算法
好吧,最小角迴歸(Least Angle Regression, LARS)演算法終於出場了。最小角迴歸法對前向梯度演算法和前向選擇演算法做了折中,保留了前向梯度演算法一定程度的精確性,同時簡化了前向梯度演算法一步步迭代的過程。具體演算法是這樣的:
首先,還是找到與因變數\(\mathbf{Y}\)最接近或者相關度最高的自變數\(\mathbf{X_k}\),使用類似於前向梯度演算法中的殘差計算方法,得到新的目標\(\mathbf{Y_{yes}}\),此時不用和前向梯度演算法一樣小步小步的走。而是直接向前走直到出現一個\(\mathbf{X_t}\),使得\(\mathbf{X_t}\)和\(\mathbf{Y_{yes}}\)的相關度和\(\mathbf{X_k}\)與\(\mathbf{Y_{yes}}\)的相關度是一樣的,此時殘差\(\mathbf{Y_{yes}}\)就在\(\mathbf{X_t}\)和\(\mathbf{X_k}\)的角平分線方向上,此時我們開始沿著這個殘差角平分線走,直到出現第三個特徵\(\mathbf{X_p}\)和\(\mathbf{Y_{yes}}\)的相關度足夠大的時候,即\(\mathbf{X_p}\)到當前殘差\(\mathbf{Y_{yes}}\)的相關度和\(\theta_t\),\(\theta_k\)與\(\mathbf{Y_{yes}}\)的一樣。將其也叫入到\(\mathbf{Y}\)的逼近特徵集合中,並用\(\mathbf{Y}\)的逼近特徵集合的共同角分線,作為新的逼近方向。以此迴圈,直到\(\mathbf{Y_{yes}}\)足夠的小,或者說所有的變數都已經取完了,演算法停止。此時對應的係數\(\theta\)即為最終結果。

當\(\theta\)只有2維時,例子如上圖,和\(\mathbf{Y}\)最接近的是\(\mathbf{X_1}\),首先在\(\mathbf{X_1}\)上面走一段距離,一直到殘差在\(\mathbf{X_1}\)和\(\mathbf{X_2}\)的角平分線上,此時沿著角平分線走,直到殘差最夠小時停止,此時對應的係數\(\beta\)即為最終結果。此處\(\theta\)計算設計較多矩陣運算,這裡不討論。
最小角迴歸法是一個適用於高維資料的迴歸演算法,其主要的優點有:
1)特別適合於特徵維度n 遠高於樣本數m的情況。
2)演算法的最壞計算複雜度和最小二乘法類似,但是其計算速度幾乎和前向選擇演算法一樣
3)可以產生分段線性結果的完整路徑,這在模型的交叉驗證中極為有用
主要的缺點是:
由於LARS的迭代方向是根據目標的殘差而定,所以該演算法對樣本的噪聲極為敏感。
6. 總結
Lasso迴歸是在ridge迴歸的基礎上發展起來的,如果模型的特徵非常多,需要壓縮,那麼Lasso迴歸是很好的選擇。一般的情況下,普通的線性迴歸模型就夠了。
另外,本文對最小角迴歸法怎麼求具體的\(\theta\)引數值沒有提及,僅僅涉及了原理,如果對具體的算計推導有興趣,可以參考Bradley Efron的論文《Least Angle Regression》,網上很容易找到。
(歡迎轉載,轉載請註明出處。歡迎溝通交流: liujianping-ok@163.com)