編碼器精度與解析度的區別
光看解析度不行的,如果分辨出的位數似乎很多但都不準,那這樣的解析度意義不大。
前些年有人用兩片8位AD拼成16位AD,表面上解析度提高了一倍,但精度並未增加,
如果這麼簡單就達到精度的提高,那AD公司光用AD0808就行了也就不必花大力氣研發16位以至更高位AD了
解析度就是你能看出A和B身高差多少,精度就是A和B身高分別是多少。
解析度是對資料的測量的精細程度,精度是準不準。
比如你用數字遊標卡尺量一個10釐米的模型,顯示結果為 50.1276釐米。
可以看出解析度挺高,精度不咋地。
解析度簡單的說就是小數點後面的位數,比如4.201V的解析度比4.20V高 但是解析度高不代表精度高
如果這個電壓本來是4.203V,高解析度測出來是4.223V,低解析度測出來是4.20V,那麼低解析度的精度高
“解析度”和“精確度”——即Resolution和Accuracy。
ADC解析度由數字化輸入訊號時所使用的位元數決定。
而精確度是指對於給定模擬輸入,實際數字輸出與理論預期數字輸出之間的接近度。
換而言之,轉換器的精確度決定了數字輸出程式碼中有多少個位元表示有關輸入訊號的有用資訊。
分辨力也稱為解析度,是指指示裝置有效地辨別緊密相鄰值的能力。
一般認為數字裝置的分辨力就是最後一位數字,模擬裝置分辨力為指示標尺分度值的一半。
測量精度是泛指測量結果的可信度,但不是規範用語。
用2.000V量程的三位半數字電壓表舉例來說,它的分辨力是0.001V,假設其精度是0.8%±3個字。
假如現在有三個個電壓的真實值是x=1.6780V,y=1.6785V,z=1.6790V。
分辨力就是,它能判別出電壓x與z之間相差0.001V,即測量z顯示的數字肯定比x大0.001;
但是它無法判別x與y之間和y與z之間的區別,即測量y時可能顯示的與x一樣,也可能顯示的與z一樣,是不確定的。
精度大概的意思就是測量值與真實值之間的最大差距。
比如,這個表測量x電壓,它可能顯示的是1.688,也可能顯示的是1.665,
也可能是別的什麼數,但是範圍不超過2.000x0.8%±3個字=±0.019V。
也就是說這個表測量x電壓時顯示1.659V-1.697V之間都算沒問題。
簡單點,做一個電壓表,10位AD測10V電壓,基本上每一格就是
10V/2^10=10/1024=0.01V,這是解析度,表示它的分辨能力是每格就是0.01V,
但是由於積分電容不好,電阻溫飄大,外部干擾,AD本身非線性等,
一個真正精確的10V電壓你測出來是9.51V(解析度決定了你最後一位小數的位置--十分位,還是百分位等),
這時你的解析度是夠高了,0.01V解析度啊,但精度呢?差了0.5/10V=5%!
總之,解析度可以上得很高,大不了增加AD位數,
你解析度小數點後位數再多,但受其它因素影響,但精度卻不能提高。
解析度通常理解為A/D轉換精度或能感知的最小變化而精度通常指:
解析度就是感測器的靈敏度,即引起輸出變化的最小輸入量,
國產溫度感測器的精度分A、B兩個級別,國標規定如下:
精度——是指在真值附近正負三倍標準差的值與量程之比,是指測量值與真值的最大差異;
關於精密度Precision 準確度Accuracy 和 解析度Resolution
一把塑料尺子,最小刻度是1mm,拿它量東西,就不能讀出1mm以下的數來,
那麼這個1mm就是它的(最小)解析度,即最小可分辨的度量。
如果已經知道一個物體的實際長度是100mm,拿這把尺子來測量,量出來的資料是102mm,
那麼這個尺子的準確度就是(102-100)/100=0.02,即測量結果與真實數值之間的誤差。
再說一個概念精密度Precision,這個是指同一個儀器每次測量數值之間的離散程度,比較的物件是自己每次測量的資料。
也用上文的尺子做測量,還是上次的那一個物體,測了5次,資料分別是108,109,107,107,108,108。
這些資料和真實值100mm之間的誤差都不小,但是這些資料之間的差距都很小,說明精密度不錯。
精密度Precision + 準確度Accuracy = 精確度。
很多人常常把 精密度Precision 誤判斷為精度,
也有些儀器廠家誤導使用者故意使用精密度代替精度。一般而言大家講的精度都是指準確度。
解析度與精度的關係能夠用下面的幾個圖證明:
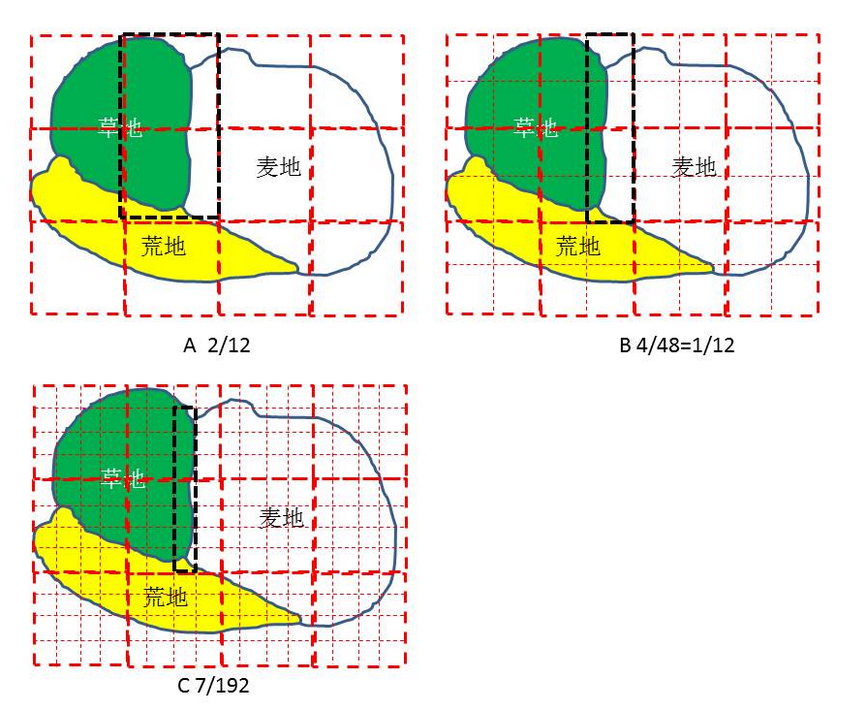

上面四個圖是相同的面積,讓我們看草地與麥地的邊界(請注意黑框中的邊界格子)。
圖A有12格子,邊界格子是2格,如此這兩個格子是不確定的,因此,不確定度是2/12。
同理,圖B中有48個格子,有四個邊界格子,如此, 不確定度是4/48。
圖C 不確定度是7/192. 圖D是不確定度是12/768。
不確定度降低,自然精度就提高,證畢
關於A/D的精度、解析度與LSB誤差的大掃盲
我們所講的精度通常是指它的精確度,其實這是錯誤的。
精度又叫做精密度,是跟準確度相對應的一個概念。
就像打靶一樣,打的準,那就說它的準確度比較高;
而每兩個靶之間能打出的偏移越小,那它的精密度就越高。
精密度 + 準確度 = 精確度。
但是鑑於大家都將精度指代了精確度,那以下所說的精度如無特別指出,都是指精確度。
很多人對於精度和解析度的概念不清楚,這裡我做一下總結,希望大家不要混淆。
我們搞電子開發的,經常跟“精度”與“解析度”打交道,這個問題不是三言兩語能搞得清楚的,在這裡只作拋磚引玉了。
簡單點說,“精度”是用來描述物理量的準確程度的,而“解析度”是用來描述刻度劃分的。
從定義上看,這兩個量應該是風馬牛不相及的。(是不是有朋友感到愕然^_^)。
很多賣感測器的JS就是利用這一點來糊弄人的了。簡單做個比喻:
有這麼一把常見的塑料尺(中學生用的那種),它的量程是10釐米,上面有100個刻度,最小能讀出1毫米的有效值。
那麼我們就說這把尺子的解析度是1毫米,或者量程的1%;
而它的實際精度就不得而知了(算是0.1毫米吧)。
當我們用火來烤一下它,並且把它拉長一段,然後再考察一下它。
我們不難發現,它還有有100個刻度,它的“解析度”還是1毫米,跟原來一樣!
然而,您還會認為它的精度還是原來的0.1毫米麼?(這個例子是引用網上的,個人覺得比喻的很形象!)
回到電子技術上,我們考察一個常用的數字溫度感測器:AD7416。
供應商只是大肆宣揚它有10位的AD,解析度是1/1024。
那麼,很多人就會這麼欣喜:哇塞,如果測量溫度0-100攝氏度,100/1024……約等於0.098攝氏度!
這麼高的精度,足夠用了。但是我們去瀏覽一下AD7416的資料手冊,居然發現裡面赫然寫著:測量精度0.25攝氏度!
所以說解析度跟精度完全是兩回事,在這個溫度感測器裡,只要你願意,你甚至可以用一個14位的AD,獲得1/16384的解析度,但是測量值的精度還是0.25攝氏度^_^
所以很多朋友一談到精度,馬上就和解析度聯絡起來了,包括有些專案負責人,只會在那裡說:這個系統精度要求很高啊,你們AD的位數至少要多少多少啊……
其實,仔細瀏覽一下AD的資料手冊,會發現跟精度有關的有兩個很重要的指標:
DNL和INL。似乎知道這兩個指標的朋友並不多,所以在這裡很有必要解釋一下。
DNL:Differencial NonLiner——微分非線性度
INL:Interger NonLiner——積分非線性度(精度主要用這個值來表示)
他表示了ADC器件在所有的數值點上對應的模擬值,和真實值之間誤差最大的那一點的誤差值。
也就是,輸出數值偏離線性最大的距離。單位是LSB(即最低位所表示的量)。
當然,像有的AD如△—∑系列的AD,也用Linearity error 來表示精度。
為什麼有的AD很貴,就是因為INL很低。
解析度同為12bit的兩個ADC,一個INL=±3LSB,而一個做到了±1.5LSB,那麼他們的價格可能相差一倍。
LSB(Least Significant Bit),意為最低有效位;
MSB(Most Significant Bit),意為最高有效位,
若MSB=1,則表示資料為負值,若MSB=0,則表示資料為正。
當選擇模數轉換器(ADC)時,最低有效位(LSB)這一引數的含義是什麼?
有位工程師告訴我某某生產商的某款12位轉換器只有7個可用位。
也就是說,所謂12位的轉換器實際上只有7位。他的結論是根據器件的失調誤差和增益誤差引數得出的,
這兩個引數的最大值如下:
失調誤差 =±3LSB,
增益誤差 =±5LSB,
乍一看,覺得他似乎是對的。從上面列出的引數可知最差的技術引數是增益誤差(±5 LSB)。
進行簡單的數學運算,12位減去5位解析度等於7位,對嗎?
果真如此的話,ADC生產商為何還要推出這樣的器件呢?
增益誤差引數似乎表明只要購買成本更低的8位轉換器就可以了,但看起來這又有點不對勁了。
正如您所判斷的,上面的說法是錯誤的。
讓我們重新來看一下LSB的定義。考慮一個12位序列轉換器,它會輸出由1或0組成的12位數串。
通常,轉換器首先送出的是最高有效位(MSB)(即LSB + 11)。有些轉換器也會先送出LSB。
在下面的討論中,我們假設先送出的是MSB(如圖1所示),
然後依次送出MSB-1 (即 LSB + 10)和MSB -2(即LSB + 9)並依次類推。
轉換器最終送出MSB -11(即LSB)作為位串的末位。
LSB這一術語有著特定的含義,它表示的是數字流中的最後一位,也表示組成滿量程輸入範圍的最小單位。
對於12位轉換器來說,LSB的值相當於模擬訊號滿量程輸入範圍除以2^12 或 4,096的商。
如果用真實的數字來表示的話,對於滿量程輸入範圍為4.096V的情況,一個12位轉換器對應的LSB大小為1mV。
但是,將LSB定義為4096個可能編碼中的一個編碼對於我們的理解是有好處的。
讓我們回到開頭的技術指標,並將其轉換到滿量程輸入範圍為4.096V的12位轉換器中:
失調誤差 = ±3LSB =±3mV,
增益誤差 =±5LSB = ±5mV,
這些技術參數列明轉換器轉換過程引入的誤差最大僅為8mV(或 8個編碼)。
這絕不是說誤差發生在轉換器輸出位流的LSB、LSB-1、LSB-2、LSB-3、LSB-4、LSB-5、LSB-6和 LSB-7 八個位上,而是表示誤差最大是一個LSB的八倍(或8mV)。
準確地說,轉換器的傳遞函式可能造成在4,096個編碼中丟失最多8個編碼。
丟失的只可能是最低端或最高階的編碼。
例如,誤差為+8LSB ((+3LSB失調誤差) + (+5LSB增益誤差)) 的一個12位轉換器可能輸出的編碼範圍為0 至 4,088。
丟失的編碼為4088至4095。相對於滿量程這一誤差很小僅為其0.2%。
與此相對,一個誤差為-3LSB((-3LSB失調誤差)—(-5LSB增益誤差))的12位轉換器輸出的編碼範圍為3至4,095。此時增益誤差會造成精度下降,但不會使編碼丟失。丟
失的編碼為0、1和2。這兩個例子給出的都是最壞情況。在實際的轉換器中,失調誤差和增益誤差很少會如此接近最大值。
在實際應用中,由於ADC失調或增益引數的改進而使效能提升的程度微不足道,甚至可以忽略。
但是,對於那些將精度作為一項設計目標的設計人員來說,這種假設太過絕對。
利用韌體設計可以很容易地實現數字校準演算法。但更重要的是,電路的前端放大/訊號調理部分通常會產生比轉換器本身更大的誤差。
通過上面的討論可以對本文開頭提到的錯誤結論有一個更為全面而清晰的認識。
事實上,上述的12位轉換器的精度約為11.997位。採用微處理器或微控制器可以利用簡單的校準演算法消除這種失調和增益誤差,這對設計人員來說無疑是個好訊息。
本文來自CSDN部落格,轉載請標明出處:http://blog.csdn.net/jhjGeneral/archive/2009/03/24/4019447.aspx
解析度和精度之間的差異。
在與使用模數轉換器 (ADC) 的系統設計人員進行交談時,我最常聽到的一個問題就是:
“你的16位ADC的精度也是16位的嗎?”
這個問題的答案取決於對解析度和精度概念的基本理解。儘管是兩個完全不同的概念,這兩個資料項經常被搞混和交換使用。
今天的博文詳述了這兩個概念間的差異。我們將在一系列帖子中深入研究造成ADC不準確的主要原因。
ADC的解析度被定義為輸入訊號值的最小變化,這個最小數值變化會改變數字輸出值的一個數值。
對於一個理想ADC來說,傳遞函式是一個步寬等於解析度的階梯。
然而,在具有較高解析度的系統中(≥16位),傳輸函式的響應將相對於理想響應有一個較大的偏離。
這是因為ADC以及驅動器電路導致的噪聲會降低ADC的解析度。
此外,如果DC電壓被施加到理想ADC的輸入上並且執行多個轉換的話,數字輸出應該始終為同樣的程式碼(由圖1中的黑點表示)。
現實中,根據總體系統噪聲(也就是包括電壓基準和驅動器電路),輸出程式碼被分佈在多個程式碼上(由下面的一團紅點表示)。
系統中的噪聲越多,資料點的集合就越寬,反之亦然。
圖1中顯示的是一箇中量程DC輸入的示例。ADC傳遞函式上輸出點的集合通常被表現為ADC資料表中的DC柱狀圖。
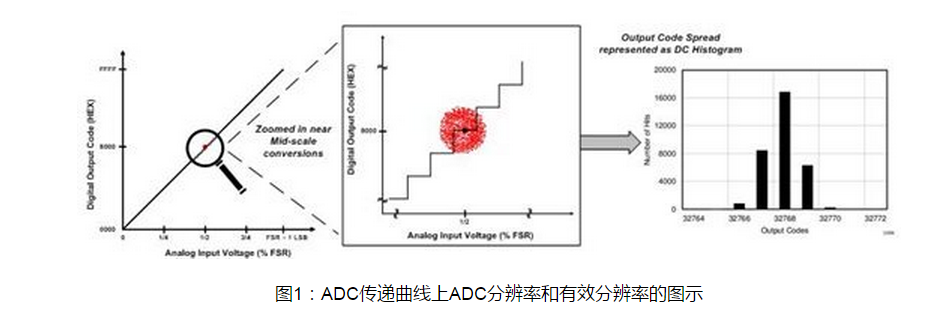
圖1中的圖表提出了一個有意思的問題。
如果同樣的模擬輸入會導致多個數字輸出,那麼對於ADC解析度的定義仍然有效嗎?
是的,前提是我們只考慮ADC的量化噪聲。
然而,當我們將訊號鏈中所有的噪聲和失真計算在內時,
正如等式 (1) 中所顯示的那樣,ADC的有效無噪聲解析度取決於輸出程式碼分佈 (NPP)。
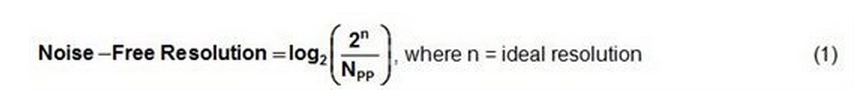
在典型ADC資料表中,有效位數 (ENOB) 間接地由AC引數和信噪失真比 (SINAD) 指定,可使用方程式2計算得出:
下面,考慮一下圖1中的輸出程式碼簇(紅點)不是位於理想輸出程式碼的中央,
而是位於遠離黑點的ADC傳遞曲線上的其他位置(如圖2中所示)。
這個距離是指示出採集系統精度。
不但ADC,還有前端驅動電路、基準和基準緩衝器都會影響到總體系統精度。
