一元、二元函式影象繪製

周見智發表於2015-09-09
函式

目錄

 

概述

本篇部落格主要是在上一篇《每個人都該懂點函數語言程式設計》的基礎上，進一步說明“函式”在函數語言程式設計中的重要作用。強調了函式和普通型別一樣，可以賦值、儲存、傳參以及作為另外函式的返回值。

本文附帶了一個Demo，該Demo可以將任意字串函式表示式解析之後生成對應的函式（一元、二元以及三元），如果你輸入的是一元或者二元函式表示式，則可以繪製出相應的函式影象。一元函式影象為平面曲線，二元函式影象為立體曲面。看下圖：

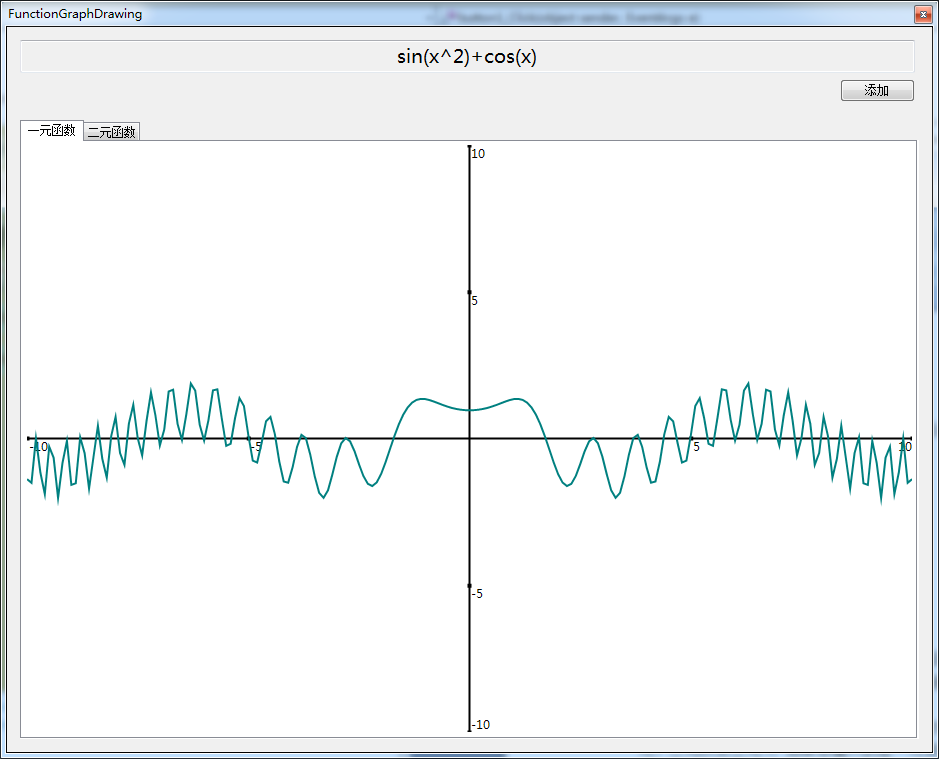
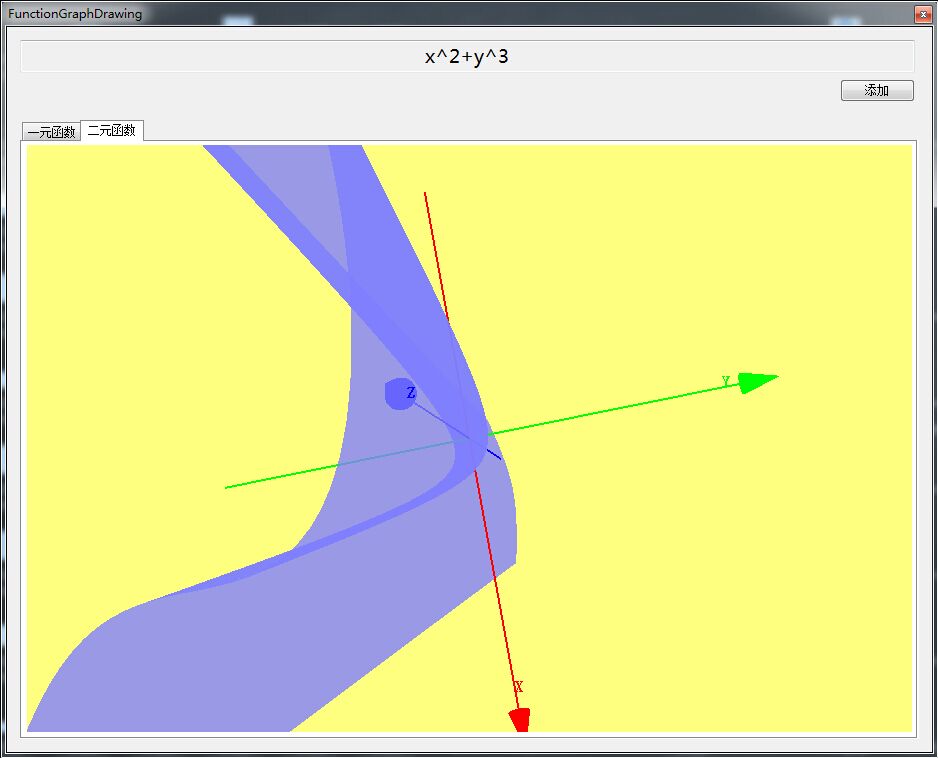
函式表示式中只識別X、Y、Z三個自變數。

Github原始碼下載

 

字串表示式解析

字串解析是重點。

怎樣去識別一串字串函式表示式呢？如x^2+sin(x)*cos(y)。之後怎樣去計算函式值呢？其實原理很簡單，由於每個函式表示式中包含的有效符號是有限的，如X、Y、Z、+、-、*、/以及一些函式諸如log、sin、cos等等，只要我們將這些有效符號均識別篩選出來之後，再根據這些符號的優先順序別生成一個函式語法樹即可。

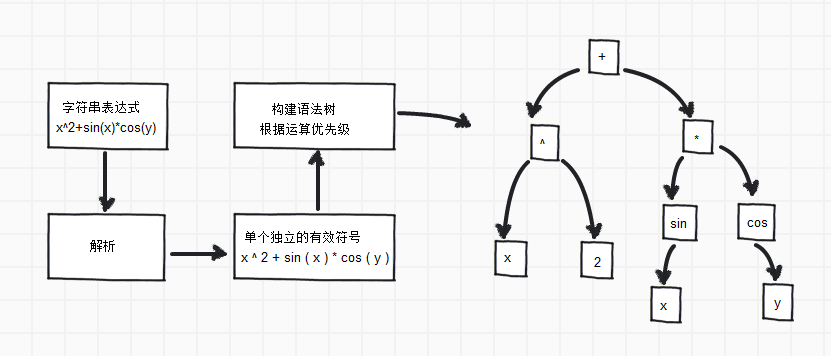
如上圖所示，使用一個“樹結構”去儲存最終的語法樹。最後帶入X、Y（二元）求得函式值。

表示式解析這塊難點是語法樹的構建和最終求值。語法樹的構建有點複雜，大家可以參見原始碼；最終求值的原理是，判斷當前符號（節點）是單目運算子號（如cos、sin、負號等）還是雙目運算子號（如+ - * /等），如果是單目運算比如cos函式，則先計運算元節點（只有一個子節點）的值，然後將得到的值進行cos運算（Math.Cos(子節點的值)）；相反，如果是雙目運算子比如+符號，那麼先計算左子節點和右子節點的值，最後將兩個值進行+操作（左子節點的值+右子節點的值），依次遞迴計算得到最終的函式值。

 

影象繪製

影象繪製這塊就比較簡單了。根據前一步得到的語法樹，我們可以建立出對應的一元函式、二元函式以及三元函式（委託的形式）。事先定義的委託結構如下：

    /// <summary>
    /// 一元函式
    /// </summary>
    /// <param name="x"></param>
    /// <returns></returns>
    public delegate double UnaryFunction(double x);
    /// <summary>
    /// 二元函式
    /// </summary>
    /// <param name="x"></param>
    /// <param name="y"></param>
    /// <returns></returns>
    public delegate double BinaryFunction(double x,double y);
    /// <summary>
    /// 三元函式
    /// </summary>
    /// <param name="x"></param>
    /// <param name="y"></param>
    /// <param name="z"></param>
    /// <returns></returns>
    public delegate double MultiFunction(double x,double y,double z);

很簡單就可以看出，一元函式接收一個引數，返回一個值；二元函式接收兩個引數，返回一個值；三元函式接收三個引數，返回一個值。生成委託的過程如下：

   (UnaryFunction)((double x) => { return root.GetValue(x, 0, 0); });
   (BinaryFunction)((double x, double y) => { return root.GetValue(x, y, 0); });
   (MultiFunction)((double x, double y, double z) => { return root.GetValue(x, y, z); });

最終給出對應的x、y、z呼叫委託，即可得到函式值。

一元函式繪製

隨便對X取一個區間（如[-10,10]），以0.1為間距，計算每個X對應的Y值（函式值）。最終將這些點連線起來，出來的就是對應的一元函式影象。

二元函式繪製

相似的，隨便對X、Y取一個區間（如X取[-10,10]，Y取[-10,10]），X、Y均以0.1為間距，計算每個（X、Y）對應的Z值（函式值），最後將這些三維點繪製成曲面。

 

函式作為屬性賦值

經過前幾步得到了函式（委託物件），我們直接將委託物件作為屬性賦給影象繪製控制元件，繪圖控制元件更新介面。

   //一元
   if (textBox1.Text.ToLower().Contains('x') && !textBox1.Text.ToLower().Contains('y') && !textBox1.Text.ToLower().Contains('z'))
   {
       UnaryFunction func = (new SyntaxManager().ParseUnaryFunction(textBox1.Text));
       unaryFunctionDrawingBoard1.Function = func;
       tabControl1.SelectedIndex = 0;
   }
   //二元
   else if (textBox1.Text.ToLower().Contains('x') && textBox1.Text.ToLower().Contains('y') && !textBox1.Text.ToLower().Contains('z'))
   {
       BinaryFunction func = (new SyntaxManager().ParseBinaryFunction(textBox1.Text));
       binaryFunctionDrawingBoard1.BinaryFunction = func;
       tabControl1.SelectedIndex = 1;
   }
   //三元
   else
   {
        MultiFunction func = (new SyntaxManager().ParseMultiFunction(textBox1.Text));
        MessageBox.Show("三元函式影象無法繪製！");
   }

如上程式碼，函式作為屬性賦值的示例。

 

參考及說明

1.Demo中有關3D圖形繪製參考了網上的一個OpenTK的demo：http://download.csdn.net/detail/dragonflies/3418135#comment

2.函式影象線上生成（為了驗證demo生成的影象是否正確）

3.注意 函式繪製時沒有做任何區間驗證，比如logX中的X不能為負,否則無效（繪製時異常）。這些需要自己注意。

 

相關文章