目錄
- 介紹
- 解決思路
- 問題一:點與線段的關係
- 問題二:線段與線段的關係
- 問題三:點與多邊形的關係
- 問題四:線段與多邊形的關係
- 總結
- 原始碼
介紹
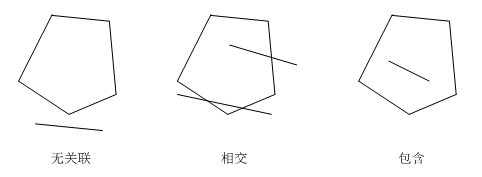
最近專案中要用到有關幾何(Geometry)方面的知識,程式需要判斷給定的一條線段(Segment)與指定多邊形(Polygon)的位置關係。這種關係分為三種:多邊形包含線段、多邊形與線段相交以及多邊形與線段無關聯。
起初我以為.NET類庫中已經包含此種判定功能的API,比如類似System.Drawing.Region這些型別,後來等到實際要用的時候才發現根本就沒這種“高階”演算法。
沒辦法,只能自己去寫程式碼實現。後來在stackoverflow(連結)上找到了一個解決方案,不過都是原始碼,並沒有詳細的說明。本文參照原作者提供的原始碼,進行詳細的說明。如果你只需要最終答案,可以不用閱讀本文所有內容,文章最後會給出判斷原始碼,很簡答使用,就一個方法,代入引數直接呼叫即可,但如果你想搞清楚怎麼回事,那麼可以靜下心來看看本文全部內容,雖然比較複雜,但是相信一定會有所收穫的。
解決思路
線段與多邊形的關係只有三種:無關聯、相交以及包含。我們可以分以下兩步來進行分析:
- 判斷線段與多邊形的各條邊是否相交,若是,則線段與多邊形屬於“相交”關係;
- 如果線段與多邊形的任何邊都不相交,那麼我們接著判斷線段的任意一個端點是否在多邊形內部,若是,則整條線段肯定在多邊形內(即“包含”關係);若不是,則整條線段肯定都在多邊形外部(即“無關聯”關係)。
上面兩步看似簡單,實質相當複雜。判斷線段與多邊形各條邊的關係涉及到了“線段與線段關係的判斷”、判斷線段任意一個端點是否在多邊形內部涉及到了“點與線段關係的判斷”,總之,要解決大問題必須先解決一些小問題:
- 點與線段的關係
- 線段與線段的關係
- 點與多邊形的關係
下面依次介紹以上三個小問題和整個大問題的解決方法。
問題一:點與線段的關係
點與線段只有兩種關係:
- 點線上段上
- 點與線段無關聯
這種判斷方法很簡單,只要我們能確保給定點P的Y座標線上段AB兩個端點的Y座標之間(或者點P的X座標在兩個端點的X座標之間也行),並且點P與線段AB任意端點間的斜率與AB線段斜率相等即可說明點P線上段AB上。
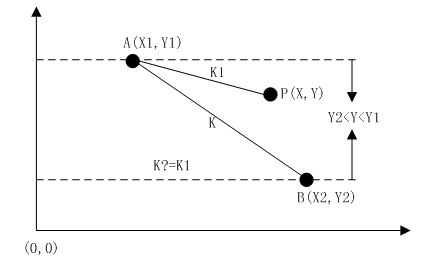
如上圖,如果Y2<Y<Y1且K==K1,則說明點P線上段AB上;否則,點P與線段AB無關聯。
問題二:線段與線段的關係
線段與線段也只有兩種關係:
- 兩線段相交
- 兩線段無關聯
這種判斷稍微複雜一些,為了更方便計算,涉及到了“平移”、“旋轉”等操作。給定線段AB和CD,先將兩線段整體平移(注意是整體),讓線段AB的A端點與原點(0,0)重合,接著將兩線段整體旋轉(注意是整體),讓線段AB與X軸的正方向重合。

如上圖,將任意兩線段AB和CD按照“先整體平移,再整體旋轉”的順序操作一遍,最終讓線段AB的A端點與原點(0,0)重合,並讓線段AB與X軸正方向重合。很顯然,任意線段均可以進行以上操作。接下來,再在此基礎上進行判斷就比較簡單了,如果線段CD的兩個端點C和D的Y座標均大於零(分佈在第一、二象限)或者均小於零(分佈在第三、四象限),那麼AB與CD肯定不相交,換句話說,CD的兩個端點必須一個在X軸上方另一個在X軸下方時,兩條線段才有可能相交。如果線段CD的端點確實是一個在X軸上方一個在X軸下方,接下來再計算直線AB和直線CD(注意這裡說的是直線)的交點(這時候兩條直線一定有交點,並且交點在X軸上),這裡暫定交點為P,如果P在X軸的負方向上(P.X<0),那麼說明線段AB和CD不相交,如果P在X軸正方向但是P的X座標大於線段AB的長度,那麼說明線段AB和CD也不相交,其他情況下,線段AB和CD才屬於“相交”關係。
問題三:點與多邊形的關係
點與多邊形有三種關係:
- 點與多邊形無關聯
- 點在多邊形上(某條邊上)
- 點在多邊形內部
判斷點是否在多邊形上需要用到解決問題一的方法,即判斷點與線段的關係。如果點不在多邊形上,那麼需要判斷它在多邊形內部還是外部,這個判斷方法說難也不難,說不難也挺難的。事實上,只需要判斷點在多邊形每條邊的左邊還是右邊(注意這裡的左邊和右邊定義,見下圖)
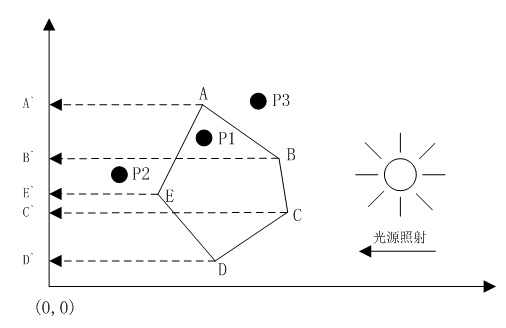
如上圖,多邊形ABCDE在右側光源的照射下,它的每條邊(如AB、BC等)都會與Y軸上各自的投影(如A`B`、B`C`等)之間形成一個梯形區域,如ABB`A`、BCC`B`等。我們只需要統計給定點P在這些梯形區域中的次數,若點P在某條邊對應的梯形區域內,那麼計數N加1,最後看N是否為偶數,如果N為偶數(包括0),那麼說明點P不在多邊形內部;否則,點P在多邊形內部。上圖中P1的計數N==1(只在ABB`A`內部),所以點P1在多邊形ABCDE內部,而點P2的計數N==2(同時在AEE`A`和BCC`B`內部),所以點P2不在多邊形ABCDE內部,同理,點P3的計數N==0,所以它也不在多邊形內部。
由上可以看出,解決問題三需要依賴問題一的解決方法。以上三個小問題都已經有解決方案了,那麼我們再來看看最開始那個問題“線段與多邊形關係”怎麼解決。
問題四:線段與多邊形關係
前三個問題解決了,這個問題其實已經很簡單了。再看一遍【解決思路】中的兩個步驟:
- 判斷線段與多邊形的各條邊是否相交,若是,則線段與多邊形屬於“相交”關係;
- 如果線段與多邊形的任何邊都不相交,那麼我們接著判斷線段的任意一個端點是否在多邊形內部,若是,則整條線段肯定在多邊形內(即“包含”關係);若不是,則整條線段肯定都在多邊形外部(即“無關聯”關係)。
我們可以使用問題二的解決方法去判斷線段是否與多邊形的各條邊相交,如果都不相交,那麼我們可以使用問題三的解決方法去判斷線段的某個端點是否在多邊形內部,如果在,那麼整個線段必然在多邊形內部;否則,整個線段必然在多邊形外部。
是的,問題四就是這麼簡單!只要我們弄懂了前三個問題的解決思路。
總結
(1)任何時候,都可以試著將大問題拆分成小問題,然後再各個擊破。大問題往往都是由許多相對簡單的小問題組成的,解決小問題肯定相對簡單。拆分問題的過程其實也是很鍛鍊人的,需要你將整個問題理清楚,先做什麼、再做什麼,再或者,做A之前是否需要先做B呢?
(2)數學與程式設計息息相關,尤其函數語言程式設計(Functional Program),可以看我前面幾篇有關函數語言程式設計的部落格:
http://www.cnblogs.com/xiaozhi_5638/category/619924.html(前幾篇)
原始碼
原始碼中包含四個方法,分別對應解決四個問題,可以去stackoverflow上看原版的,也可以看下面:

1 /// <summary> 2 /// 與幾何相關的輔助類 3 /// </summary> 4 public static class GeometryHelper 5 { 6 /// <summary> 7 /// 判斷線段與多邊形的關係 8 /// </summary> 9 /// <param name="line"></param> 10 /// <param name="polygon"></param> 11 /// <returns></returns> 12 public static Intersection IntersectionOf(Line line, Polygon polygon) 13 { 14 if (polygon.Length == 0) 15 { 16 return Intersection.None; 17 } 18 if (polygon.Length == 1) 19 { 20 return IntersectionOf(polygon[0], line); 21 } 22 bool tangent = false; 23 for (int index = 0; index < polygon.Length; index++) 24 { 25 int index2 = (index + 1) % polygon.Length; 26 Intersection intersection = IntersectionOf(line, new Line(polygon[index], polygon[index2])); 27 if (intersection == Intersection.Intersection) 28 { 29 return intersection; 30 } 31 if (intersection == Intersection.Tangent) 32 { 33 tangent = true; 34 } 35 } 36 return tangent ? Intersection.Tangent : IntersectionOf(line.P1, polygon); 37 } 38 /// <summary> 39 /// 判斷點與多邊形的關係 40 /// </summary> 41 /// <param name="point"></param> 42 /// <param name="polygon"></param> 43 /// <returns></returns> 44 public static Intersection IntersectionOf(PointF point, Polygon polygon) 45 { 46 switch (polygon.Length) 47 { 48 case 0: 49 return Intersection.None; 50 case 1: 51 if (polygon[0].X == point.X && polygon[0].Y == point.Y) 52 { 53 return Intersection.Tangent; 54 } 55 else 56 { 57 return Intersection.None; 58 } 59 case 2: 60 return IntersectionOf(point, new Line(polygon[0], polygon[1])); 61 } 62 63 int counter = 0; 64 int i; 65 PointF p1; 66 int n = polygon.Length; 67 p1 = polygon[0]; 68 if (point == p1) 69 { 70 return Intersection.Tangent; 71 } 72 73 for (i = 1; i <= n; i++) 74 { 75 PointF p2 = polygon[i % n]; 76 if (point == p2) 77 { 78 return Intersection.Tangent; 79 } 80 if (point.Y > Math.Min(p1.Y, p2.Y)) 81 { 82 if (point.Y <= Math.Max(p1.Y, p2.Y)) 83 { 84 if (point.X <= Math.Max(p1.X, p2.X)) 85 { 86 if (p1.Y != p2.Y) 87 { 88 double xinters = (point.Y - p1.Y) * (p2.X - p1.X) / (p2.Y - p1.Y) + p1.X; 89 if (p1.X == p2.X || point.X <= xinters) 90 counter++; 91 } 92 } 93 } 94 } 95 p1 = p2; 96 } 97 98 return (counter % 2 == 1) ? Intersection.Containment : Intersection.None; 99 } 100 /// <summary> 101 /// 判斷點與直線的關係 102 /// </summary> 103 /// <param name="point"></param> 104 /// <param name="line"></param> 105 /// <returns></returns> 106 public static Intersection IntersectionOf(PointF point, Line line) 107 { 108 float bottomY = Math.Min(line.Y1, line.Y2); 109 float topY = Math.Max(line.Y1, line.Y2); 110 bool heightIsRight = point.Y >= bottomY && 111 point.Y <= topY; 112 //Vertical line, slope is divideByZero error! 113 if (line.X1 == line.X2) 114 { 115 if (point.X == line.X1 && heightIsRight) 116 { 117 return Intersection.Tangent; 118 } 119 else 120 { 121 return Intersection.None; 122 } 123 } 124 float slope = (line.X2 - line.X1) / (line.Y2 - line.Y1); 125 bool onLine = (line.Y1 - point.Y) == (slope * (line.X1 - point.X)); 126 if (onLine && heightIsRight) 127 { 128 return Intersection.Tangent; 129 } 130 else 131 { 132 return Intersection.None; 133 } 134 } 135 /// <summary> 136 /// 判斷直線與直線的關係 137 /// </summary> 138 /// <param name="line1"></param> 139 /// <param name="line2"></param> 140 /// <returns></returns> 141 public static Intersection IntersectionOf(Line line1, Line line2) 142 { 143 // Fail if either line segment is zero-length. 144 if (line1.X1 == line1.X2 && line1.Y1 == line1.Y2 || line2.X1 == line2.X2 && line2.Y1 == line2.Y2) 145 return Intersection.None; 146 147 if (line1.X1 == line2.X1 && line1.Y1 == line2.Y1 || line1.X2 == line2.X1 && line1.Y2 == line2.Y1) 148 return Intersection.Intersection; 149 if (line1.X1 == line2.X2 && line1.Y1 == line2.Y2 || line1.X2 == line2.X2 && line1.Y2 == line2.Y2) 150 return Intersection.Intersection; 151 152 // (1) Translate the system so that point A is on the origin. 153 line1.X2 -= line1.X1; line1.Y2 -= line1.Y1; 154 line2.X1 -= line1.X1; line2.Y1 -= line1.Y1; 155 line2.X2 -= line1.X1; line2.Y2 -= line1.Y1; 156 157 // Discover the length of segment A-B. 158 double distAB = Math.Sqrt(line1.X2 * line1.X2 + line1.Y2 * line1.Y2); 159 160 // (2) Rotate the system so that point B is on the positive X axis. 161 double theCos = line1.X2 / distAB; 162 double theSin = line1.Y2 / distAB; 163 double newX = line2.X1 * theCos + line2.Y1 * theSin; 164 line2.Y1 = (float)(line2.Y1 * theCos - line2.X1 * theSin); line2.X1 = (float)newX; 165 newX = line2.X2 * theCos + line2.Y2 * theSin; 166 line2.Y2 = (float)(line2.Y2 * theCos - line2.X2 * theSin); line2.X2 = (float)newX; 167 168 // Fail if segment C-D doesn't cross line A-B. 169 if (line2.Y1 < 0 && line2.Y2 < 0 || line2.Y1 >= 0 && line2.Y2 >= 0) 170 return Intersection.None; 171 172 // (3) Discover the position of the intersection point along line A-B. 173 double posAB = line2.X2 + (line2.X1 - line2.X2) * line2.Y2 / (line2.Y2 - line2.Y1); 174 175 // Fail if segment C-D crosses line A-B outside of segment A-B. 176 if (posAB < 0 || posAB > distAB) 177 return Intersection.None; 178 179 // (4) Apply the discovered position to line A-B in the original coordinate system. 180 return Intersection.Intersection; 181 } 182 } 183 /// <summary> 184 /// 幾何體之間的關係型別 185 /// </summary> 186 public enum Intersection 187 { 188 None, 189 Tangent, 190 Intersection, 191 Containment 192 }
