程式設計正規化(Programming paradigm)
程式設計正規化指我們在編寫程式解決問題的思路和視角。它提供了同時也決定了程式設計師對程式執行的看法。計算機程式設計中存在許多程式設計正規化,如指令式程式設計、宣告式程式設計、物件導向程式設計以及結構化程式設計等等。其中物件導向程式設計正規化認為程式是由一系列相互作用的物件組成,而結構化程式設計正規化認為程式採用子程式、程式碼區塊、for迴圈以及while迴圈等結構組成。下面主要說明本篇文章將要講到的指令式程式設計正規化和宣告式程式設計正規化。
1)指令式程式設計(Imperative):
強調程式程式碼模擬電腦執行過程,強調“先做什麼”、“再做什麼”。如果我們要計算“2*3+1”,我們編寫程式碼時先計算2*3存入臨時變數,再計算該臨時變數與1的和。指令式程式設計是當前主流程式設計正規化,我們編寫的程式碼幾乎都屬於指令式程式設計正規化。
2)宣告式程式設計(Declarative):
強調程式程式碼模擬人腦計算過程,強調“最終要什麼”,相比指令式程式設計正規化來講,它更看重結果而非過程。宣告式程式設計正規化更接近人類思想,它的思考層面要高於指令式程式設計。
下圖顯示了指令式程式設計正規化與宣告式程式設計正規化的區別:
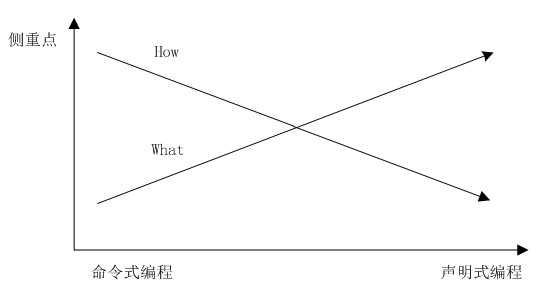
圖1
注:各種程式設計正規化之間並非都是對立的,很多正規化是從不同角度來劃分的。如物件導向程式設計正規化同時也屬於指令式程式設計正規化。當然,本篇文章講到的“指令式程式設計正規化”和“宣告式程式設計正規化”兩者是對立的。
宣告式程式設計正規化
宣告式程式設計正規化常見有以下兩種(最常見):
1)領域特定語言(Domain Specific Language,DSL):
名字很陌生,但是我們卻經常在用。如SQL、CSS以及正規表示式等等。這些語言只在特定領域起作用,並且使用這些語言時,我們大多數時候是在寫“陳述、宣告”的語句。如“select * from tb”,我們只關心我們要的結果,而不用去關係具體實現。
2)函數語言程式設計(Functional Program,FP):
函數語言程式設計是我們要討論的重點。既然它屬於宣告式程式設計正規化,那麼它也應該強調結果(What)而非過程(How)。沒錯,函數語言程式設計不同於常見的指令式程式設計,它不關心計算機具體的實現過程,而僅僅注重問題結果。
函數語言程式設計(Functional Program):
網上關於“函數語言程式設計”的解釋有很多,但大多數都比較模糊抽象。維基百科上對函數語言程式設計的解釋是“In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data”,翻譯成中文就是“函數語言程式設計是一種程式設計正規化,它將計算機運算看作是數學中函式的計算,並且避免了狀態以及變數的概念”。這是個什麼意思呢?很多文章分別從函數語言程式設計的幾個特點上做出瞭解釋,比如“函式是第一公民”、“高階函式(Higher Order Function)”、“無狀態性(No State)”、“無副作用性(Side-Effect)”、“易於並行開發”以及“惰性求值”等等。但是我覺得這些都只是函數語言程式設計的特點或者說是優點,並沒有實質上解釋出“函數語言程式設計”與普通指令式程式設計的區別。我認為要搞清楚函數語言程式設計,必須先認清“函式”的概念。沒錯,雖然我們自認為我們比較熟悉“函式”(或者叫“方法”,本文不區分這兩者的區別),但是我們真的熟悉它們嗎?
注:以後部落格將依次介紹“函數語言程式設計”以上幾種特點。
程式設計函式和數學函式:
第一次瞭解“函式”的概念應該是我們讀中學時,“y=x+1”在平面座標系中是一條直線,到後來(不知道哪年級)學習了二次函式,“y=x^2+2*x+1”在平面座標系中是一條拋物線。當時學習函式時知道以下知識點:
1)函式是一種對映,自變數經由一種對映關係變換後,得到因變數(函式值);
2)對於每個自變數,均能、有且僅有一個因變數與之對應,這是函式的確定性。也就是說,給定一個自變數,任何時候函式值都唯一;
那麼,到大學學習程式設計後(本人讀大學才開始學習程式設計),我們在程式中又遇見了“函式”,很熟悉的感覺。但是它和數學中的函式有什麼關聯呢?也就是說,數學思想與我們程式設計思想是否有關聯?如果以我們目前寫C#、Java、C++等程式碼來看,它們幾乎沒有關係,因為我們程式中的函式可以沒有引數(數學函式中的“自變數”),也可以沒有返回值(數學函式中的因變數),就算一個函式有返回值,那麼給定引數,呼叫函式後每次執行結果也可能不一樣。以上這些均不能滿足數學函式的概念。其實出現“兩種函式幾乎無關係”的現象很容易理解,數學描述的是人類思維過程,而我們(目前大部分人)編寫的程式程式碼描述的是計算機執行過程。在數學家與程式設計師之間早已產生了溝通障礙,比如下圖:
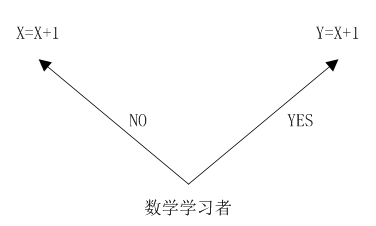
圖2
如上圖所示,“X=X+1”這種表示式如果從數學角度來看,幾乎是不可成立的,讓任何一個沒有學過程式設計的人去看這個表示式,TA都會以為你寫的是錯的,他們只認“Y=X+1”。原因很簡單,在程式中,符號可以代表變數,而變數表示一個記憶體單元,該記憶體處的值可以被重寫(賦值);而在數學中,符號永遠只是符號,等號“=”兩邊表示等價關係,“Y=X+1”表示Y與X+1是等價的,Y僅僅是X+1的一個代替符號。
同理,函式也一樣。數學中的函式僅僅描述一種“對映關係”,給定一個自變數,我們可以得到一個因變數,僅此而已。而程式中的函式更多的時候扮演的是一種“功能”角色,它能夠完成指定任務。當然,如果程式中一個函式包含引數,並且能夠返回值,那麼它完全可以模擬數學函式。下面使用C#編寫一個委託,它代表數學中的一個一元函式:
1 public delegate double Function1X(double x);
如上程式碼所示,委託簽名中包含一個double型別引數,並且返回一個double型別返回值。數學中的“f(x)=x^2+2*x+1”可以使用C#編寫以下函式:
1 public double f(double x) 2 { 3 return Math.Pow(x,2) + 2*x + 1; 4 }
函式f(x)在x=2處的值呼叫程式碼:f(2);。或者使用Lambda表示式:
x => Math.Pow(x,2) + 2*x + 1;
程式中的函式接收一個double型別引數,經過對映關係,返回一個double型別的返回值,它與“f(x)=x^2 + 2*x +1”對應。那麼數學函式中的二元函式在程式中怎樣表示呢?很簡單,二元函式包含兩個自變數,我們只需要為程式中函式定義兩個引數即可:
1 public delegate double Function2XY(double x,double y);
如上程式碼所示,委託簽名中包含兩個double型別引數,並且返回一個double型別返回值。
從上面的介紹可以看出,如果將程式中函式做一些限制,那麼它就可以模擬數學中的函式了:
1)每個函式必須包含輸入引數(作為自變數);
2)每個函式必須有返回值(作為因變數);
3)無論何時,給定引數呼叫函式時,返回值必須一致。
上面第三條限制是為了滿足函式的“確定性”,該條限制要求程式中的函式執行期間不能依賴於外界因素,也不要影響外部環境。換句話說,它在執行期間與外界是隔絕的。我們將滿足以上條件的函式稱為“純函式(Pure Function)”。純函式與外界互動只有一條渠道——傳入引數與返回值。純函式也不讀取/改變全域性變數、無IO操作等。

圖3
純函式是程式程式碼模擬數學函式的基礎。理論上講,函數語言程式設計中,函式是第一公民的同時,所有函式也都應該屬於“純函式”。到此,我們再回過頭看一下維基百科上對“函數語言程式設計”的解釋:函數語言程式設計是一種程式設計正規化,它將計算機運算看作是數學中函式的計算,並且避免了狀態以及變數的概念。很顯然,函數語言程式設計向數學驗算靠攏,使用一種平時正常的數學思維去解決問題。
注:函數語言程式設計是基於“lambda驗算(Lambda Calculus)”的,它並不屬於“圖靈機”理論範疇。我沒搞清楚lambda驗算,所以本文並沒詳細提到。看到Lambda很容易讓我們想到C#3.0中引入的Lambda表示式,這不是偶然。C# 3.0之後開始支援“函數語言程式設計”,後面文章將會講到。
(未完待續)