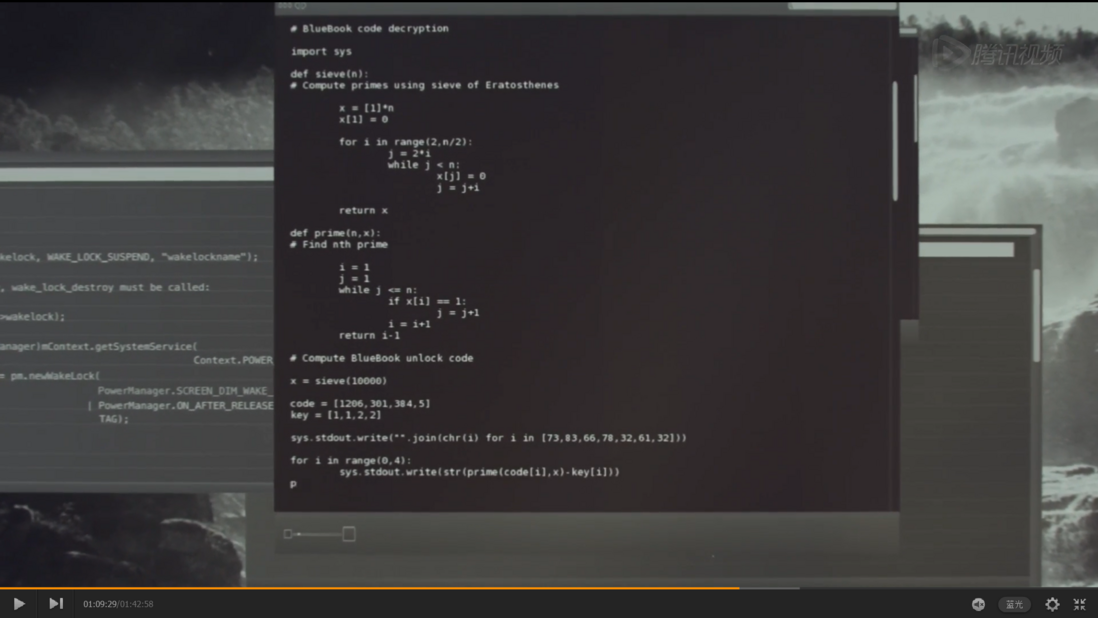
今天看了《機械姬》,探討人工智慧話題的電影,豆瓣評分7.5,還是蠻不錯的一部電影。影片1:09:29處出現了一段python程式碼,細看了一下,發現是篩法求質數的python程式碼,寫得非常簡練的。先貼個電影的截圖:
影片裡的程式碼略微有點模糊,我重新打一遍,是下面這個樣子的
#coding:utf8
import sys
def sieve(n):
#compute primes using sieve eratosthenes
x = [1] * n
x[1] = 0
for i in range(2,n/2):
j = 2 * i
while j < n:
x[j] = 0
j = j + i
return x
def prime(n,x):
#Find nth prime
i = 1
j = 1
while j <= n:
if x[i] == 1:
j = j + 1
i = i + 1
return i-1
x = sieve(10000)
code = [1206,301,384,5]
key = [1,1,2,2]
sys.stdout.write("".join(chr(i) for i in [73,83,66,78,32,61,22]))
for i in range(0,4):
sys.stdout.write(str(prime(code[i],x)-key[i]))程式碼的最後列印出來下面這個很奇怪的東西,目測是一本書的ISBN,上豆瓣查了一下,是Embodiment and the Inner Life,是關於思維、意識的內容的,和本片的主題息息相關。
ISBN =9780199226559[Finished in 0.1s]
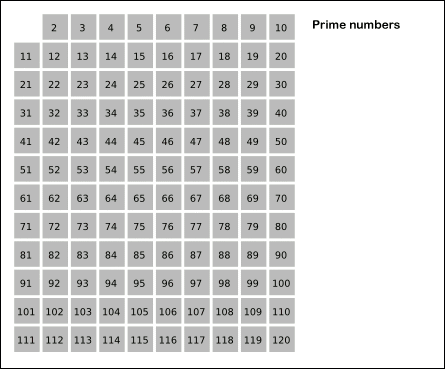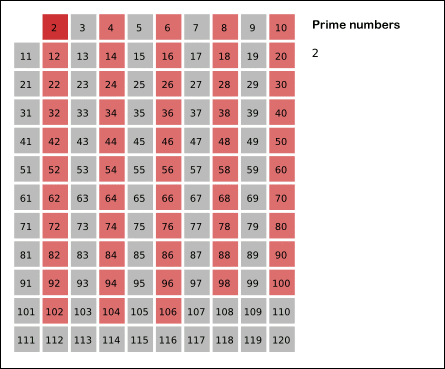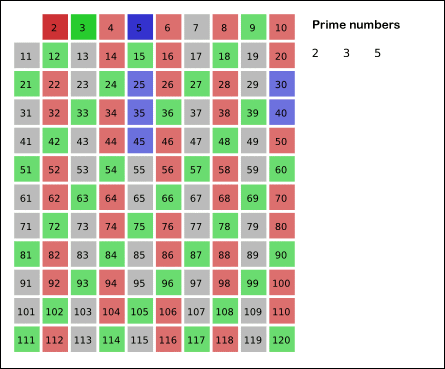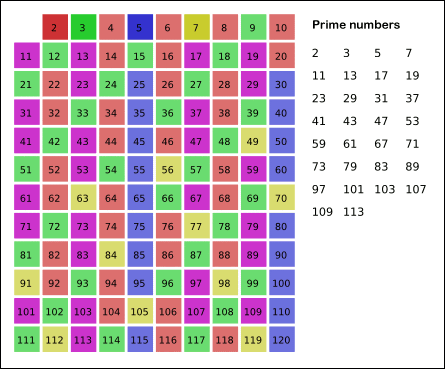
重點還是前面的兩個函式實現的篩法求質數。首先介紹一下什麼是篩法,篩法相傳是古希臘的埃拉託斯特尼發明的一種檢測素數的演算法。篩法的思路非常簡單,可以用下面的動圖來描述。給定一個範圍,首先用2去篩,把所有2的倍數都篩掉,然後再用3篩,用5篩,不斷重複下去......
再來看程式碼
def sieve(n): //對n以內的數進行篩選,返回一個長度為n的布林陣列 #compute primes using sieve eratosthenes x = [1] * n //定義長度為n的布林陣列(實際上電影裡用1和0來表示true和false了) x[1] = 0 //1既不是素數也不是合數,設為0 for i in range(2,n/2)://i從2開始一直到n/2 j = 2 * i //j從2倍i開始 while j < n: x[j] = 0 //把所有i的倍數篩除 j = j + i //下一個i的倍數 return x //返回陣列 def prime(n,x): //求第n個素數,只需要在篩選好的布林陣列中找第n個標記為1的數就可以了 #Find nth prime i = 1 //初始化為1 j = 1 while j <= n: //在布林陣列中尋找第n個標記為1的數 if x[i] == 1: j = j + 1 i = i + 1 return i-1 //前面迴圈中i多加了一次,返回時需要減1
可以看到,使用篩法求第n個質數的時間複雜度為O(n),缺點在需要提前求得篩選的結果,增加了空間複雜度,篩選結果可以用位元位來表示以節省空間。
此外還有一個問題,在求第n個質數的時候,如何要確定第n個質數的大致範圍,以確定篩選結果的布林陣列長度。根據素數定理,可以用來估算某個範圍內的素數個數,可以用公式x/ln(x)來描述,ln表示自然對數,假設要估計10000以內有多少質數,代入公式10000/ln(10000)得到的結果為1085.73,使用上面的篩法得到的10000以為的質數個數為1229,可以看到估計值比實際值略小一點,估計的範圍越大,估計值與實際值的誤差越小。實際使用中可以透過公式計算估計值,然後按一定百分比擴大範圍即可。
文章轉自: http://segmentfault.com/a/1190000004162829