地圖點聚合優化方案

zhanlijun發表於2015-04-11

http://www.cnblogs.com/LBSer/p/4417127.html

一、為什麼需要點聚合

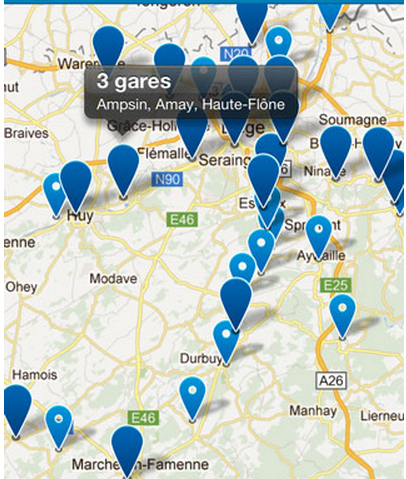
在地圖上查詢結果通常以標記點的形式展現，但是如果標記點較多，不僅會大大增加客戶端的渲染時間，讓客戶端變得很卡，而且會讓人產生密集恐懼症（圖1）。為了解決這一問題，我們需要一種手段能在使用者有限的可視區域範圍內，利用最小的區域展示出最全面的資訊，而又不產生重疊覆蓋。

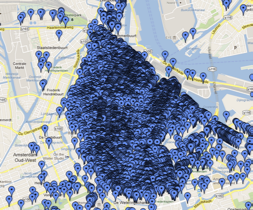
圖1

二、已嘗試的方案---kmeans

直覺上用聚類演算法能較好達成我們目標，因此採用簡單的kmeans聚類。根據客戶端的請求，我們知道了客戶端顯示的範圍，併到索引引擎裡取出在此範圍內的資料，並對這些資料進行kmeans聚類，最後將結果返回給客戶端。

但是上線之後發現kmeans效果並不如意，主要有以下兩個缺點。

a）效能問題

kmeans是計算密集型演算法，需要迭代多次才能完成，而且每次迭代過程中都涉及到複雜的距離計算，比較消耗cpu。

我們在上線後遇到load較高的問題。

b）效果問題

kmeans未能徹底解決重疊覆蓋問題！可以看到有些聚合後的圖示會疊合在一起。

三、優化方案

再次回顧我們的目的：我們需要一種手段能在使用者有限的可視區域範圍內，利用最小的區域展示出最全面的資訊，而又不產生重疊覆蓋。

3.1. 直接網格法

解決地理空間相關問題時，對空間劃分網格這種方法往往屢試不爽。

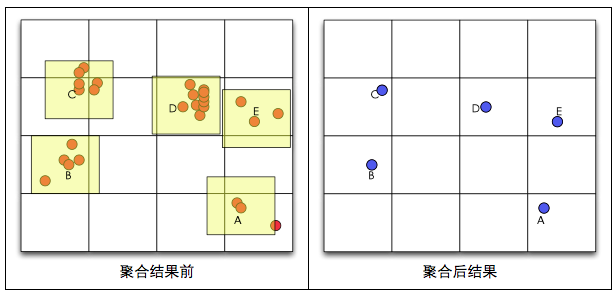
原理：將地圖範圍劃分成指定尺寸的正方形（每個縮放級別不同尺寸），然後將落在對應格子中的點聚合到該正方形中（正方形的中心），最終一個正方形內只顯示一箇中心點，並且點上顯示該聚合點所包含的原始點的數量。

如何將點落到正方形內呢？我們將空間人為指定100*100大小，通過這個公式進行對映。

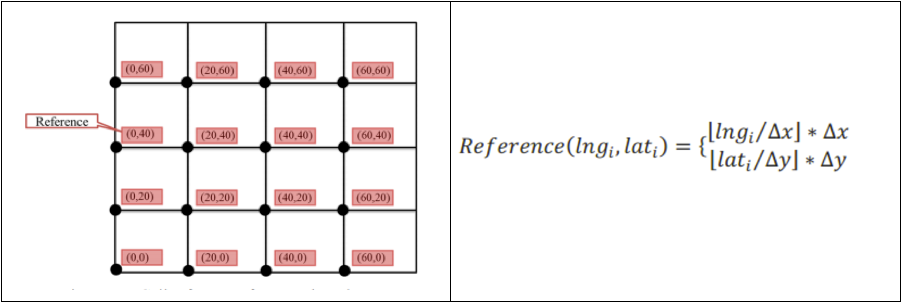
優點：運算速度較快，每個原始點只需計算一次，沒有複雜的距離計算。

缺點：有時明明很相近的點，卻僅僅因為網路的分界線而被逼分開在不同的聚合點中，此外，聚合點的位置採用的是該網格的中心，而非該網格的質心，這樣聚合出來的點可能不能較精確反映原始點的資訊。

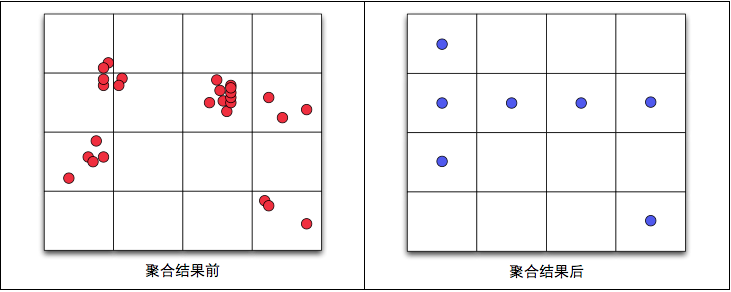
3.2. 網格距離法

原理：沿用方案一思想，1）將各個點落到相應正方形內；2）求解各個網格的質心；3）合併質心：判斷各個質心是否在某一範圍內，如果在某一範圍內則進行合併。

如何判斷各個質心點是否需要合併呢？以A點為例，畫一個矩形或者圓範圍，落在此範圍內的合併，B、C均落在範圍內，因此A、B、C三點合併。

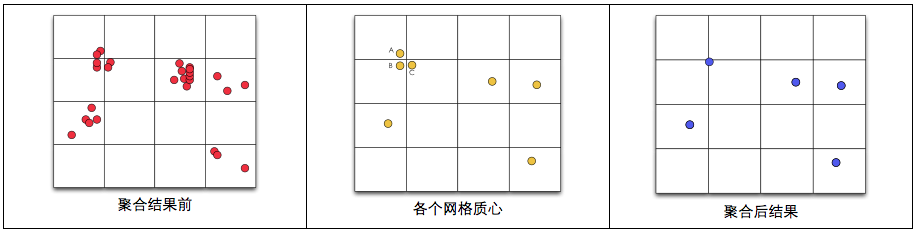
優點：運算速度同樣較快，相對於方案一，多了求解質心以及質心合併兩個步驟，但這兩個步驟都較為簡單，能很快完成。

3.3. 直接距離法

原理：初始時沒有任何已知聚合點，然後對每個點進行迭代，計算一個點的外包正方形，若此點的外包正方形與現有的聚合點的外包正方形不相交，則新建聚合點（這裡不是計算點與點間的距離，而是計算一個點的外包正方形，正方形的變長由使用者指定或程式設定一個預設值），若相交，則把該點聚合到該聚合點中，若點與多個已知的聚合點的外包正方形相交，則計算該點到到聚合點的距離，聚合到距離最近的聚合點中，如此迴圈，直到所有點都遍歷完畢。每個縮放級別都重新遍歷所有原始點要素。

優點：運算速度相對較快，每個原始點只需計算一次，可能會有點與點距離計算，聚合點較精確的反映了所包含的原始點要素的位置資訊。

缺點：速度不如完全基於網格的速度快等，此法還有個缺點，就是各個點迭代順序不同導致最終結果不同。因此涉及到制定迭代順序的問題。