經典演算法面試題(二)

1 . 大整數乘法

下面先介紹“列表法”:
例如當計算8765*234時，把乘數和被乘數照如下列出，見表：

8	7	6	5	*
16	14	12	10	2
24	21	18	15	3
32	28	24	20	4

16	14	12	10
	24	21	18	15
		32	28	24	20
16	38	65	56	39	20

	16	38	65	56	39	20
2	16+4=20	38+7=45	65+6=71	56+4=60	39+2=41
留2	留0進2	留5進4	留1進7	留0進6	留1進4	留0進2
2	0	5	1	0	1	0

根據以上思路 就可以編寫C++程式了，再經分析可得：

1，一個m位的整數與一個n位的整數相乘，乘積為m+n-1位或m+n位。
2，程式中，用三個字元陣列分別儲存乘數，被乘數與乘積。由第1點分析知，存放乘積的字元陣列餓長度應不小於存放乘數與被乘數的兩個陣列的長度之和。
3，可以把第二步“計算填表”與第三四步“累加進位”放在一起完成，可以節省儲存表格2所需的空間。
4，程式關鍵部分是兩層迴圈，內層迴圈累計一陣列的和，外層迴圈處理保留的數字和進位。

#include <iostream>
#include <string>

using namespace std;

int  resualt[2048] = { 0 };
string num1, num2;

void multiply(string n1,string n2)
{
    int n1len = n1.length();
    int n2len = n2.length();
    int sum = 0;
    int carry = 0;
    int i, j;
    for (i = n1len + n2len-2; i >=0; i--)
    {
        sum = carry;
        j = i - n1len+1;
        if (j < 0)
            j = 0;
        for (; j <= i&&j <= n2len-1; j++)
            sum += (n1[i - j] - '0')*(n2[j] - '0');
        resualt[i+1] = sum % 10;
        carry = sum / 10;
    }
    if (carry>0)
        resualt[0] = carry ;
}

int main()
{
    cin >> num1 >> num2;
    multiply(num1, num2);
    for (int y = 0; y <num1.length() + num2.length(); y++)
        cout << resualt[y];
    return 0;
}

演算法改進：
8216547*96785 將兩數從個位起，每3位分為節，列出乘法表，將斜線間的數字相加：

8	216	547
	96	785

8	216	547	*
768	20736	52512	96
6250	169560	429395	785

768	20736	52512
	6250	169560	429395
768	27016	222072	429395

將表中最後一行進行如下處理：從個位數開始，每一個方格里只保留三個數字，超出1000的部分進位到前一個方格里：

768	27016	222072	429395
768+27=795	27016+222=27238	222072+429=222501	留395進429
795	238	501	395

所以8216547*96785 = 795238501395

也就是說我們在計算生成這個二維表時，不必一位一位的乘，而可以三位三位的乘；在累加時也是滿1000進位。這樣，我們計算m位整數乘以n位整數，只需要進行m*n/9次乘法運算，再進行約（m+n）/3次加法運算和（m+n）/3次去摸運算。總體看來，效率是前一種演算法的9倍。

2 . 哈夫曼樹

定義哈夫曼樹之前先說明幾個與哈夫曼樹有關的概念：

路徑： 樹中一個結點到另一個結點之間的分支構成這兩個結點之間的路徑。
路徑長度：路徑上的分枝數目稱作路徑長度。
樹的路徑長度：從樹根到每一個結點的路徑長度之和。
結點的帶權路徑長度：在一棵樹中，如果其結點上附帶有一個權值，通常把該結點的路徑長度與該結點上的權值 之積稱為該結點的帶權路徑長度（weighted path length）
樹的帶權路徑長度：如果樹中每個葉子上都帶有一個權值，則把樹中所有葉子的帶權路徑長度之和稱為樹的帶
                               權路徑長度。

設某二叉樹有n個帶權值的葉子結點，則該二叉樹的帶權路徑長度記為：

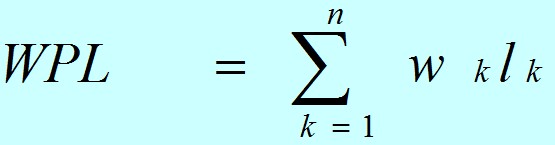
公式中，Wk為第k個葉子結點的權值；Lk為該結點的路徑長度。
示例：

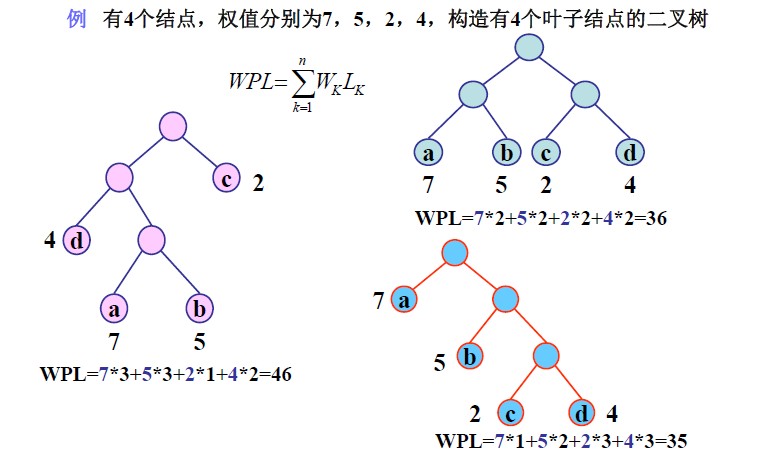
根據哈弗曼樹的定義，一棵二叉樹要使其WPL值最小，必須使權值越大的葉子結點越靠近根結點，而權值越小的葉子結點
越遠離根結點。
哈弗曼依據這一特點提出了一種構造最優二叉樹的方法，其基本思想如下：

下面演示了用Huffman演算法構造一棵Huffman樹的過程：

3 . 由一個等概率的隨機函式生成另一個等概率的隨機函式

知有個rand7()的函式，可以生成等概率的[1,7]範圍內的隨機整數，讓利用這個rand7()構造rand10()函式，生成等概率的[1,10]範圍內的隨機整數。

已知有個rand7()的函式，可以生成等概率的[1,7]範圍內的隨機整數，讓利用這個rand7()構造rand10()函式，生成等概率的[1,10]範圍內的隨機整數。

分析：要保證rand10()在整數1-10的均勻分佈，可以構造一個1-10*n的均勻分佈的隨機整數區間（n為任何正整數）。假設x是這個1-10*n區間上的一個隨機整數，那麼x%10+1就是均勻分佈在1-10區間上的整數。由於(rand7()-1)*7+rand7()可以構造出均勻分佈在1-49的隨機數（原因見下面的說明），可以將41～49這樣的隨機數剔除掉，得到的數1-40仍然是均勻分佈在1-40的，這是因為每個數都可以看成一個獨立事件。
下面說明為什麼(rand7()-1)*7+rand7()可以構造出均勻分佈在1-49的隨機數:
首先rand7()-1得到一個離散整數集合{0，1，2，3，4，5，6}，其中每個整數的出現概率都是1/7。那麼(rand7()-1)*7得到一個離散整數集合A={0，7，14，21，28，35，42}，其中每個整數的出現概率也都是1/7。而rand7()得到的集合B={1，2，3，4，5，6，7}中每個整數出現的概率也是1/7。顯然集合A和B中任何兩個元素組合可以與1-49之間的一個整數一一對應，也就是說1-49之間的任何一個數，可以唯一確定A和B中兩個元素的一種組合方式，反過來也成立。由於A和B中元素可以看成是獨立事件，根據獨立事件的概率公式P(AB)=P(A)P(B)，得到每個組合的概率是1/7*1/7=1/49。因此(rand7()-1)*7+rand7()生成的整數均勻分佈在1-49之間，每個數的概率都是1/49。

int rand_10()    
{    
    int x = 0;    
    do    
    {    
        x = 7 * (rand7() - 1) + rand7();    
    }while(x > 40);    
    return x % 10 + 1;    
}

另一種思路：第一個數由rand7()產生，第二個由rand7()+1產生，，，第10個由(rand7()+9)%10產生，由於是等概率的，以此迴圈，也生成的等概率的1-10之間的隨機數。

4 . 字串匹配演算法

字串匹配演算法一般有樸素的字串匹配演算法，Rabin-Karp演算法，優先自動機的演算法以及KMP演算法，其中最經典的就是KMP演算法。
首先看下KMP演算法的執行過程：
舉例說明，如下是使用上例的模式串對目標串執行匹配的步驟

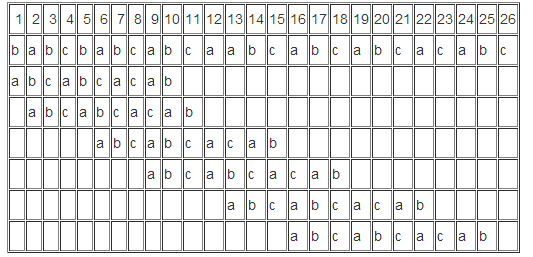
通過模式串的5次移動，完成了對目標串的模式匹配。這裡以匹配的第3步為例
此時pattern串的第1個字母與target[6]對齊，從6向後依次匹配目標串，到target[13]時發現target[13]=’a’，而pattern[8]=’c’，匹配失敗，此時next[8]=5，所以將模式串向後移動8-next[8] = 3個字元，將pattern[5]與target[13]對齊，然後由target[13]依次向後執行匹配操作。在整個匹配過程中，無論模式串如何向後滑動，目標串的輸入字元都在不會回溯，直到找到模式串，或者遍歷整個目標串都沒有發現匹配模式為止。
next跳轉表，在進行模式匹配，實現模式串向後移動的過程中，發揮了重要作用。這個表看似神奇，實際從原理上講並不複雜，對於模式串而言，其字首字串，有可能也是模式串中的非字首子串，這個問題我稱之為字首包含問題。以模式串abcabcacab為例，其字首4 abca，正好也是模式串的一個子串abc(abca)cab，所以當目標串與模式串執行匹配的過程中，如果直到第8個字元才匹配失敗，同時也意味著目標串當前字元之前的4個字元，與模式串的前4個字元是相同的，所以當模式串向後移動的時候，可以直接將模式串的第5個字元與當前字元對齊，執行比較，這樣就實現了模式串一次性向前跳躍多個字元。所以next表的關鍵就是解決模式串的字首包含。
下面給出該演算法的偽碼：

KMP-MATCHER(T,P)
n<-length(T)
m<-length(P)
next<-COMPUTE-PREFIX-FUNCTION(P)
q<-0
for i<-1 to n
    do while q>0 and P[q+1]!=T[i]
        do q<-next[q]
       if P[q+1]=T[i]
           then q<-q+1
       if q=m
           then print "Pattern occurs with shift" i<-m
           q<-next[q]

COMPUTE-PREFIX-FUNCTION(P)
m<-length(P)
next[1]<-0
k<-0
for q<-2 to m
    do while k>0 and P[k+1]!=P[q]
        do k<-next[k]
    if P[k+1]=P[q]
        then k<-k+1
    next[q]<-k
return next

KMP演算法的時間複雜度為O(m+n).