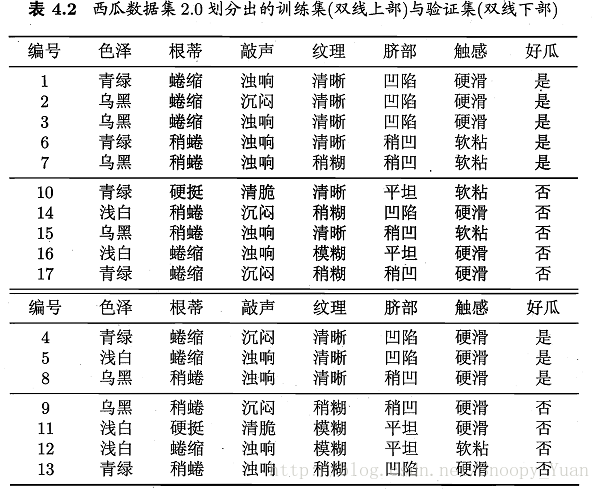
周志華《機器學習》課後習題解答系列（五）：Ch4.4 - 程式設計實現CART演算法與剪枝操作

這裡主要基於Python實現，許多地方採用了sklearn庫，環境搭建可參考 資料探勘入門：Python開發環境搭建（eclipse-pydev模式）.

相關答案和原始碼託管在我的Github上：PY131/Machine-Learning_ZhouZhihua.

4.4 程式設計實現CART演算法與剪枝操作

• 決策樹基於訓練集完全構建易陷入過擬合。為提升泛化能力。通常需要對決策樹進行剪枝。

• 原始的CART演算法採用基尼指數作為最優屬性劃分選擇標準。

編碼基於Python實現，詳細解答和編碼過程如下：（檢視完整程式碼和資料集）：

1.最優劃分屬性選擇 - 基尼指數

同資訊熵類似，基尼指數（Gini index）也常用以度量資料純度，一般基尼值越小，資料純度越高，相關內容可參考書p79，最典型的相關決策樹生成演算法是CART演算法。

下面是某屬性下資料的基尼指數計算程式碼樣例（連續和離散的不同操作）：

def GiniIndex(df, attr_id):
    '''
    calculating the gini index of an attribution

    @param df:      dataframe, the pandas dataframe of the data_set
    @param attr_id: the target attribution in df
    @return gini_index: the gini index of current attribution
    @return div_value: for discrete variable, value = 0
                   for continuous variable, value = t (the division value)
    '''  
    gini_index = 0  # info_gain for the whole label
    div_value = 0  # div_value for continuous attribute

    n = len(df[attr_id])  # the number of sample

    # 1.for continuous variable using method of bisection
    if df[attr_id].dtype == (float, int):
        sub_gini = {}  # store the div_value (div) and it's subset gini value

        df = df.sort([attr_id], ascending=1)  # sorting via column
        df = df.reset_index(drop=True)

        data_arr = df[attr_id]
        label_arr = df[df.columns[-1]]

        for i in range(n-1):
            div = (data_arr[i] + data_arr[i+1]) / 2
            sub_gini[div] = ( (i+1) * Gini(label_arr[0:i+1]) / n ) \
                              + ( (n-i-1) * Gini(label_arr[i+1:-1]) / n )
        # our goal is to get the min subset entropy sum and it's divide value
        div_value, gini_index = min(sub_gini.items(), key=lambda x: x[1])

    # 2.for discrete variable (categoric variable)
    else:
        data_arr = df[attr_id]
        label_arr = df[df.columns[-1]]
        value_count = ValueCount(data_arr)

        for key in value_count:
            key_label_arr = label_arr[data_arr == key]
            gini_index += value_count[key] * Gini(key_label_arr) / n

    return gini_index, div_value

---

2.完全決策樹生成

下圖是基於基尼指數進行最優劃分屬性選擇，然後在資料集watermelon-2.0全集上遞迴生成的完全決策樹。(基礎演算法和流程可參考題4.3，或檢視完整程式碼）

---

3.剪枝操作

參考書4.3節（p79-83），剪枝是提高決策樹模型泛化能力的重要手段，一般將剪枝操作分為預剪枝、後剪枝兩種方式，簡要說明如下：

剪枝型別	搜尋方向	方法開銷	結果樹的大小	擬合風險	泛化能力
預剪枝（prepruning）	自頂向下	小（與建樹同時進行）	很小	存在欠擬合風險	較強
後剪枝（postpruning）	自底向上	較大（決策樹已建好）	較小		很強

基於訓練集與測試集的劃分，程式設計實現預剪枝與後剪枝操作：

3.1 完全決策樹

下圖是基於訓練集生成的完全決策樹模型，可以看到，在有限的資料集下，樹的結構過於複雜，模型的泛化能力應該很差：

此時在測試集（驗證集）上進行預測，精度結果如下：

accuracy of full tree: 0.571

3.2 預剪枝

參考書p81，採用預剪枝生成決策樹，檢視相關程式碼， 結果樹如下：

現在的決策樹退化成了單個節點，（比決策樹樁還要簡單），其測試精度為：

accuracy of pre-pruning tree: 0.571

此精度與完全決策樹相同。進一步分析如下：

• 基於奧卡姆剃刀準則，這棵決策樹模型要優於前者；
• 由於資料集小，所以預剪枝優越性不明顯，實際預剪枝操作是有較好的模型提升效果的。
• 此處結果模型太簡單，有嚴重的欠擬合風險。

3.3 後剪枝

參考書p83-84 ，採用後剪枝生成決策樹，檢視相關程式碼，結果樹如下：

決策樹相較完全決策樹有了很大的簡化，其測試精度為：

accuracy of post-pruning tree: 0.714

此精度相較於前者有了很大的提升，說明經過後剪枝，模型泛化能力變強，同時保留了一定樹規模，擬合較好。

4.總結

• 由於本題資料集較差，決策樹的總體表現一般，交叉驗證存在很大波動性。
• 剪枝操作是提升模型泛化能力的重要途徑，在不考慮建模開銷的情況下，後剪枝一般會優於預剪枝。
• 除剪枝外，常採用最大葉深度約束等方法來保持決策樹泛化能力。

---