神經網路基礎 - PyBrain機器學習包的使用

---

PyBrain = Python-Based Reinforcement Learning, Artificial Intelligence and Neural Network，是一個基於Python的以神經網路為核心的機器學習包。這裡我們用它來實現一個基本的BP神經網路。

安裝準備

PyBrain安裝十分簡單（只是要提前裝好依賴包numpy，scipy，nose等）：

1. 由於PyBrain託管在GitHub上，可直接使用git命令來獲取最新版本：

   git clone git://github.com/pybrain/pybrain.git "指定路徑"
   

2. 進入指定路徑，執行安裝命令：

   python setup.py install
   

   安裝可能需要許可權。

更多安裝資訊可參考官方主頁-Installation.

資料準備

這裡我們採用UCI著名資料集Iris Data Set.

其資料集的簡述如下：

輸入：鳶尾花的四個屬性（連續值）
    1. sepal length in cm
    2. sepal width in cm
    3. petal length in cm
    4. petal width in cm

輸出：鳶尾花的品種（分類值）
    -- Iris Setosa
    -- Iris Versicolour
    -- Iris Virginica

過程：由輸入預測輸出

其他：
    樣本量：150，每類樣本量平均。
    缺失值：無

下面是一些資料示例：

5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
...
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
...
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
...

模型學習 - 基於PyBrain

檢視完整程式碼

資料預處理

這裡要採用BP神經網路（多層前饋神經網路）來構建IRIS預測模型（分類器），先對資料進行分析。

1. 讀取並檢視資料：

   已安裝的sklearn包自帶iris資料集，並且已將輸出型別從字串（Iris-setosa，Iris-versicolor，Iris-virginica）轉化為離散數（0，1，2），方便計算操作。

2. 資料歸一化處理：

   資料共有4個輸入屬性（特徵），一個輸出類別標籤，各屬性單位均是cm（連續值、同度量），故不考慮進行歸一化處理。

3. 進一步分析：

   通過視覺化可以對資料進行相關性檢驗。同時檢視資料點及標籤分散情況，從而對分類難度和分類器維度有一個初步的感知。

   下圖所示為採用matplotlib繪製的前兩個屬性的散點圖：

   

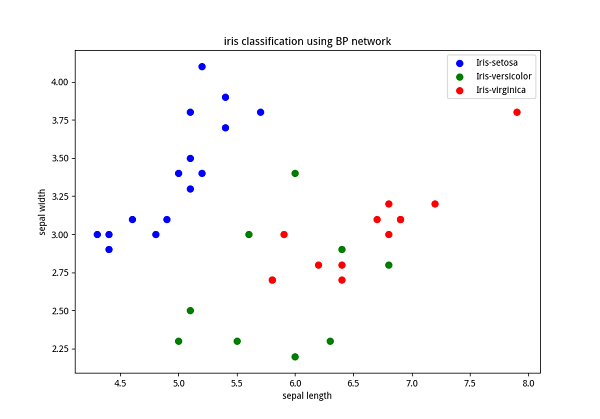
   從這些圖中可以得出線性不可分等基本認識。

4. 獨熱編碼：

   由於輸出為離散標稱值，考慮採用獨熱編碼（one hot encoding）將其轉換為數值變數。pybrain自帶獨熱編碼函式datasets.ClassificationDataSet_convertToOneOfMany()。編碼前後輸出變數示意如下：

   編碼前：

   [[1],
    [2],
    [1],
    [0]]
   

   編碼後：

   [[0, 1, 0],
    [0, 0, 1],
    [0, 1, 0],
    [1, 0, 0]]
   

   可以看到編碼後，神經網路的輸出從1維變到3維，所以輸出節點數設為3，為了讓輸出對映類別標籤，可採用softmax函式作為輸出層的啟用函式。

5. 程式示例：

   下面是讀取資料並進行編碼的程式示例（包括訓練集測試集的劃分）：

'''
preparation of data
'''
from sklearn import datasets  
iris_ds = datasets.load_iris()
X, y = iris_ds.data, iris_ds.target
label = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']

from pybrain.datasets import ClassificationDataSet
# 4 input attributes, 1 output with 3 class labels
ds = ClassificationDataSet(4, 1, nb_classes=3, class_labels=label)  
for i in range(len(y)): 
    ds.appendLinked(X[i], y[i])
ds.calculateStatistics()

# split training, testing, validation data set (proportion 4:1)
tstdata_temp, trndata_temp = ds.splitWithProportion(0.25)  
tstdata = ClassificationDataSet(4, 1, nb_classes=3, class_labels=label)
for n in range(0, tstdata_temp.getLength()):
    tstdata.appendLinked( tstdata_temp.getSample(n)[0], tstdata_temp.getSample(n)[1] )

trndata = ClassificationDataSet(4, 1, nb_classes=3, class_labels=label)
for n in range(0, trndata_temp.getLength()):
    trndata.appendLinked( trndata_temp.getSample(n)[0], trndata_temp.getSample(n)[1] )

# one hot encoding
trndata._convertToOneOfMany()
tstdata._convertToOneOfMany()

BP網路訓練

採用pybrain包訓練BP神經網路模型的基本步驟如下：

• 初始化網路（設定層數、每層節點數、每層啟用函式等），示例程式碼如下：

from pybrain.tools.shortcuts import buildNetwork
# 4 input nodes, 3 output node each represent one class
# here we set 5 hidden layer nodes.
# SoftmaxLayer(0/1) for multi-label output activation function
n_h = 5
net = buildNetwork(4, n_h, 3, outclass = SoftmaxLayer)  

• 初始化訓練子（如訓練模型物件，訓練集等），進行訓練（設定迭代次數（epoch引數），批處理或流處理（batchlearning引數）），示例程式碼如下：

# standard(incremental) BP algorithm: 
trainer = BackpropTrainer(net, trndata)
trainer.trainEpochs(1)

上述程式碼是採用一次資料集遍歷的**標準BP演算法**，若採用多次迭代直至收斂的**累積BP演算法**，示例程式碼如下（50次迭代，標準梯度下降）：

# accumulative BP algorithm: 
trainer = BackpropTrainer(net, trndata, batchlearning=True)
err_train, err_valid = trainer.trainUntilConvergence(maxEpochs=500)

模型驗證

直接在測試集上進行預測，計算輸出精度（累積BP演算法下可檢視收斂曲線）：

'''
test of model
'''
# convergence curve 
import matplotlib.pyplot as plt
plt.plot(err_train,'b',err_valid,'r')
plt.show()

# model testing
from pybrain.utilities import percentError
tstresult = percentError( trainer.testOnClassData(), tstdata['target'] )
print("epoch: %4d" % trainer.totalepochs, " test error: %5.2f%%" % tstresult)   

標準BP演算法在IRIS測試集上的精度結果如下所示：

epoch:    1  test error:  0.88%

可以看出，錯誤率＜1%，說明該模型精度表現良好（和資料集本身高維可分也有很大的關係）。

累積BP演算法下，得出引數收斂曲線如下圖所示：

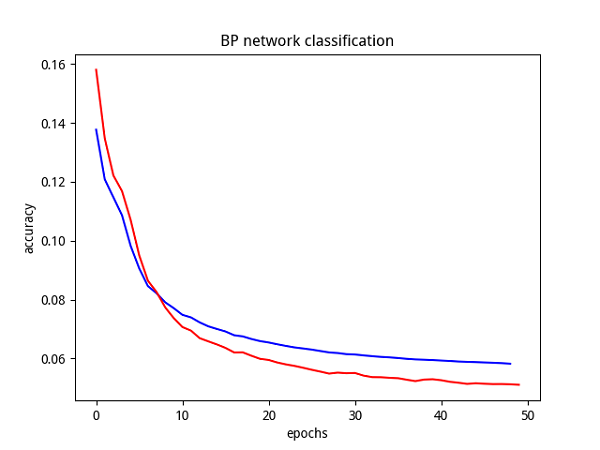
可以看出，累積BP演算法的引數收斂良好，預測精度結果比標準BP演算法還要好一些。

但是，採用datetime測試程式執行時間，可以看出累積BP演算法遠遠大於標準BP演算法。

總結

採用pybrain可以輕鬆實現一些基本的神經網路模型，方便了神經網路的實現練習。

ps.這個包本身的執行效率貌似也不是特別高。

參考

本文內容主要參考了官方文件：

• PyBrain官方文件主頁