周志華《機器學習》課後習題解答系列（六）：Ch5.5 - BP演算法實現

這裡的程式設計基於Python-PyBrain。Pybrain是一個以神經網路為核心的機器學習包，相關內容可參考神經網路基礎 - PyBrain機器學習包的使用

相關答案和原始碼託管在我的Github上：PY131/Machine-Learning_ZhouZhihua.

5.5 BP演算法實現

實驗過程：基於PyBrain分別實現標準BP和累積BP兩種演算法下的BP網路訓練，並進行比較；

1.演算法分析

參考書上推導及演算法圖5.8，首先給出BP演算法的兩種版本示意如下：

Algorithms 1. 標準BP演算法
----
    輸入： 訓練集 D，學習率 η.
    過程： 
        1. 隨即初始化連線權與閾值 (ω，θ).
        2. Repeat：
        3.   for x_k，y_k in D:
        4.     根據當前引數計算出樣本誤差 E_k.
        5.     根據公式計算出隨機梯度項 g_k.
        6.     根據公式更新 (ω，θ).
        7.   end for
        8. until 達到停止條件
    輸出：(ω，θ) - 即相應的多層前饋神經網路.
----

Algorithms 2. 累積BP演算法
----
    輸入： 訓練集 D，學習率 η，迭代次數 n.
    過程： 
        1. 隨即初始化連線權與閾值 (ω，θ).
        2. Repeat：
        3.     根據當前引數計算出累積誤差 E.
        4.     根據公式計算出標準梯度項 g.
        5.     根據公式更新 (ω，θ).
        6.     n = n-1
        7. until n=0 or 達到停止條件
    輸出：(ω，θ) - 即相應的多層前饋神經網路.
----

可以看出，兩種演算法的本質區別類似於隨機梯度下降法與標準梯度下降法的區別。pybrain包為我們實現這兩種不同的演算法提供了方便。我們只需要修改 pybrain.supervised.trainers 的初始化引數（如learningrate、batchlearning）並設定資料集遍歷次數 trainEpochs() 即可。

2.資料預處理

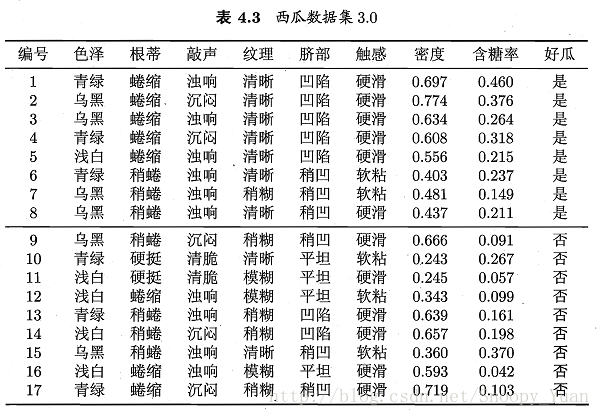
從表4.3的西瓜資料集3.0可以看到，樣本共有8個屬性變數和一個輸出變數。其中既有標稱變數（色澤~觸感、好瓜），也有連續變數（密度、含糖率）。

為了方便進行神經網路模型的搭建（主要是為對離散值進行數值計算），首先考慮對標稱變數進行數值編碼，這裡我們採用pandas.get_dummies()函式進行輸入的獨熱編碼（轉化為啞變數的形式），採用pybrain.datasets.ClassificationDataSet的_convertToOneOfMany()進行輸出的獨熱編碼。關於獨熱編碼原理可參考One-hot_Wikipedia或資料預處理之獨熱編碼（One-Hot Encoding）

對“西瓜資料集3.0”進行獨熱編碼：

編碼前：

編號  色澤  根蒂  敲聲  紋理  臍部  觸感     密度    含糖率 好瓜
0    1  青綠  蜷縮  濁響  清晰  凹陷  硬滑  0.697  0.460  是
1    2  烏黑  蜷縮  沉悶  清晰  凹陷  硬滑  0.774  0.376  是
2    3  烏黑  蜷縮  濁響  清晰  凹陷  硬滑  0.634  0.264  是
...

此時資料集大小[17,10]，8輸入，1輸出。

編碼後：

編號     密度    含糖率  色澤_烏黑  色澤_淺白  色澤_青綠  根蒂_硬挺  根蒂_稍蜷  根蒂_蜷縮  敲聲_沉悶  ...   \
0    1  0.697  0.460      0      0      1      0      0      1      0  ...    
1    2  0.774  0.376      1      0      0      0      0      1      1  ...    
2    3  0.634  0.264      1      0      0      0      0      1      0  ...   
... 

紋理_模糊  紋理_清晰  紋理_稍糊  臍部_凹陷  臍部_平坦  臍部_稍凹  觸感_硬滑  觸感_軟粘  好瓜_否  好瓜_是  
0       0      1      0      1      0      0      1      0     0     1  
1       0      1      0      1      0      0      1      0     0     1  
2       0      1      0      1      0      0      1      0     0     1  
...

此時資料集大小[17,22]，19輸入，2輸出。

3.模型訓練與測試

根據上面的資料，搭建一個19輸入，2輸出的前向反饋神經網路（BP network）。然後劃分訓練集與測試集，進行建模與驗證實驗。

實現說明，在pybrain中：splitWithProportion函式可直接劃分資料；buildNetwork函式可用於搭建BP神經網路；BackpropTrainer用於生成訓練模版並可基於此進行訓練，改變相關引數可分別實現標準BP演算法和累積BP演算法；

生成模型，pybrain預設的是Sigmoid啟用函式，其非常適用於二分類，另外還有一種啟用函式十分適用於多分類（包括二分類），即Softmax function。這裡我們將輸出進行了獨熱編碼，因此考慮採用Softmax作為輸出層的啟用函式，然後採用勝者通吃（winner-takes-all）法則確定分類結果。

模型生成樣例程式碼：
```
n_h = 5 # hidden layer nodes number
net = buildNetwork(19, n_h, 2, outclass = SoftmaxLayer)
```

標準BP演算法學習神經網路：

樣例程式碼：

trainer = BackpropTrainer(net, trndata)
trainer.trainEpochs(1)

累積BP演算法學習神經網路樣例程式碼（50次迭代）：

樣例程式碼：
```
trainer = BackpropTrainer(net, trndata, batchlearning=True)
trainer.trainEpochs(50) 
```
此外還可以繪製出累積BP演算法引數學習過程的收斂曲線，檢視詳細程式碼：
兩種演算法比較：

上述兩種BP演算法實現的程式碼區別可參考PyBrain官網: trainers – - Supervised Training for Networks and other Modules

進行一次訓練，然後基於測試集預測，得出兩種方法的預測精度如下：
```
標準BP演算法： epoch:    1  test error: 50.00%
累積BP演算法： epoch:   50  test error: 25.00%
```
可以看出，本次實驗累積BP演算法優於前者，但一次實驗說服力不夠，於是我們進行多次實驗得出預測結果平均精度比較如下：
```
標準BP演算法：
25.00%  75.00%  75.00%  75.00%  50.00%  50.00% ... 
average error rate: 47.50%

累積BP演算法：
25.00%  75.00%  50.00%  50.00%  25.00%  50.00% ...
average error rate: 38.75%
```
從結果可以看出，累積BP演算法精度總體還是優於標準BP演算法。但在實驗過程中我們注意到，累積BP演算法的執行時間遠大於標準BP演算法。

進一步地，我們注意到，由於資料集限制（樣本量太少），模型精度很差。

4.參考

本文涉及到的一些重要參考如下：