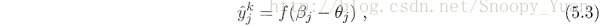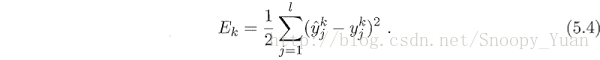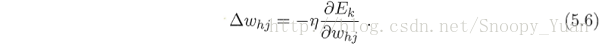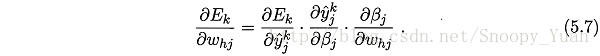神經網路基礎 - Python程式設計實現標準BP演算法

程式設計基於python，完整程式碼託管在我的Github PY131/Practice-of-Machine-Learning，歡迎訪問。

基礎知識參考“周志華《機器學習》第五章-神經網路”

1. BP演算法分析

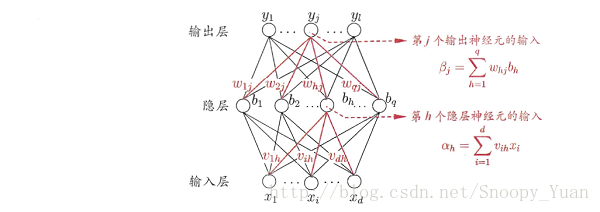
如下圖所示BP網路：

對樣本 a = (x_k,y_k)，其輸出為 ^y_k，即是：

由此得出在樣本 a 上的均方誤差：

我們的目標是是所有樣本得出的均方誤差最小化，為此我們要找到最優的引數（即上圖中的連線權(w, v)及對應閾值(θ, γ)）。考慮梯度下降法。比如對於 w = w+Δw，梯度下降法調整式為：

式中，η 是學習率，他控制著演算法迭代步長，直接關係著演算法的收斂速度甚至收斂性。

對於圖示BP網路，梯度項有：

其中：

當採用Sigmoid函式作為每個神經元的啟用函式是，可以根據其導數性質：

來得出最終的梯度項 g_j*b_h，其中：

於是得出BP演算法關於引數 w 的更新公式：

同樣的方式可以推匯出其他引數的更新公式，綜上，可以得出BP演算法中引數的更新公式如下：

其中：

經過上面的推導，給出標準BP演算法如下圖所示：

Algorithm 1. 標準BP演算法
----
    輸入： 訓練集 D，學習率 η.
    過程： 
        1. 隨即初始化連線權與閾值 (ω，θ).
        2. Repeat：
        3.   for x_k，y_k in D:
        4.     根據當前引數計算出樣本誤差 E_k.
        5.     根據公式計算出隨機梯度項 g_k.
        6.     根據公式更新 (ω，θ).
        7.   end for
        8. until 達到停止條件
    輸出：(ω，θ) - 即相應的多層前饋神經網路.
----

2. BP演算法程式設計實現

採用python程式設計實現上面的演算法，首先明確一些需求：

• 程式應保留神經網路結構調整的靈活性，主要面向隱層節點數的變動；
• 程式應保留啟用函式過載功能，此處先採用Sigmoid啟用函式；
• 程式應保留學習率設定功能，此處先採用固定學習率實現；
• 程式應具有快速高效，如考慮python-numpy進行高效的矩陣運算；
• …

下面是簡單的標準BP演算法程式示例：

def BackPropagate(self, x, y, lr):
    '''
    the implementation of BP algorithms on one slide of sample

    @param x, y: array, input and output of the data sample
    @param lr: float, the learning rate of gradient decent iteration
    '''

    # dependent packages
    import numpy as np 

    # get current network output
    self.Pred(x)

    # calculate the gradient based on output
    o_grid = np.zeros(self.o_n) 
    for j in range(self.o_n):
        o_grid[j] = (y[j] - self.o_v[j]) * self.afd(self.o_v[j])

    h_grid = np.zeros(self.h_n)
    for h in range(self.h_n):
        for j in range(self.o_n):
            h_grid[h] += self.ho_w[h][j] * o_grid[j]
        h_grid[h] = h_grid[h] * self.afd(self.h_v[h])   

    # updating the parameter
    for h in range(self.h_n):  
        for j in range(self.o_n): 
            self.ho_w[h][j] += lr * o_grid[j] * self.h_v[h]

    for i in range(self.i_n):  
        for h in range(self.h_n): 
            self.ih_w[i][h] += lr * h_grid[h] * self.i_v[i]     

    for j in range(self.o_n):
        self.o_t[j] -= lr * o_grid[j]    

    for h in range(self.h_n):
        self.h_t[h] -= lr * h_grid[h]

完整的程式實現點選檢視

3. 分類實驗

完整實驗程式

這裡我們採用sklearn自帶的資料集生成器Samples generator中的make_circles和make_moons()函式來生成兩個二分類的非線性可分資料集：

資料集生成程式示例（生成circles資料）：

# 生成circle資料集，並新增一定的噪聲  
from sklearn.datasets import make_circles 
X, y = make_circles(100, noise=0.10)  # 2 input 1 output

資料點如下圖所示：

從圖中可以看出，資料是二分類非線性可分的。採用神經網路對其分類模式進行學習是個不錯的選擇。

生成BP網路並初始化，這裡通過程式設計實現的一個BP網路類，各種操作及相關變數在類中定義。

下面是搭建網路並訓練的示例程式：

nn = BP_network()  # build a BP network class
nn.CreateNN(2, 6, 1, 'Sigmoid')  # build the network # 隱層節點數為6

for i in range(500): # 迭代500次
    err, err_k = nn.TrainStandard(X, y.reshape(len(y),1), lr=0.5)

經過大量的迭代訓練，可以觀察出神經網路在訓練樣本上的誤差收斂情況，如下圖示（由於circles的分類較困難一些，故而其上的迭代進行的次數多一些）：

最總得出的分類決策區域繪製如下圖：

可以看出，神經網路的分類決策區域還是比較精確的，進一步，為考慮所訓練的模型的泛化效能，可將資料集拆分為訓練集與測試集進行重新訓練與測試，並可以採用交叉驗證法等方法。

4. 小結

這裡基於python程式設計實現了標準BP演算法，並採用兩種有趣的資料集來進行的實驗。這裡給出實驗中的一些總結：

• BP神經網路訓練往往需要大量的計算（體現在迭代次數多，矩陣運算規模大等）；
• 標準BP演算法對引數較為敏感，如學習率，迭代次數，隱層節點數等都需要注意；
• 一般來說，足夠多隱層節點的BP網路能夠逼近任意目標函式，但訓練資料集的不充分性始終存在，要特別注意過擬合問題。