引言：

在關聯分析中，頻繁項集的挖掘最常用到的就是Apriori演算法。Apriori演算法是一種先產生候選項集再檢驗是否頻繁的“產生-測試”的方法。這種方法有種弊端：當資料集很大的時候，需要不斷掃描資料集造成執行效率很低。
而FP-Growth演算法就很好地解決了這個問題。它的思路是把資料集中的事務對映到一棵FP-Tree上面，再根據這棵樹找出頻繁項集。FP-Tree的構建過程只需要掃描兩次資料集。
更多關聯分析和Apriori演算法的資訊請見：什麼是關聯分析、Apriori演算法的介紹。

正言：

我們還是用購物籃的資料：

TID	Items
001	Cola, Egg, Ham
002	Cola, Diaper, Beer
003	Cola, Diaper, Beer, Ham
004	Diaper, Beer

TID代表交易流水號，Items代表一次交易的商品。

首先，FP-Growth演算法的任務是找出資料集中的頻繁項集。
然後，FP-Growth演算法的步驟，大體上可以分成兩步：(1)FP-Tree的構建； (2)FP-Tree上頻繁項集的挖掘。

FP-Tree的構造：

1. 掃描一遍資料庫，找出頻繁項的列表 L
   L
   ，按照支援度計數遞減排序。即：
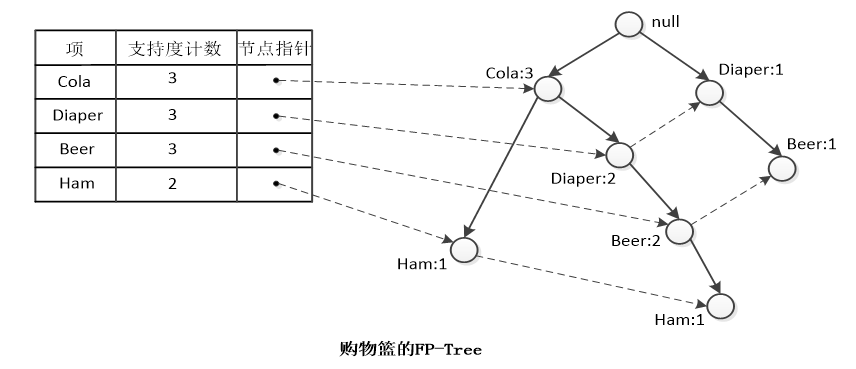
   L
   L
   = <(Cola:3), (Diaper:3), (Beer:3), (Ham:2)>
2. 再次掃描資料庫，由每個事務不斷構建FP-Tree：
   ①FP-Tree的根節點為 null 。
   ②從資料庫中取出事務，按照 L
   L
   排序，然後把每個項逐個新增到FP-Tree的分枝上去。例如，事務001排序後為{Cola, Ham}，在根節點上加一棵子樹Cola-Ham。事務002排序後為{Cola, Diaper, Beer}，因為根節點上已經有個子樹節點“Cola”，所以可以共用該節點，在Cola節點上加一棵子樹Diaper-Beer，同時Cola的計數加1。事務003可與樹共用節點Cola-Diaper-Beer，所以只需在Beer後面加個子樹節點“Ham”，同時把Cola、Diaper、Beer的計數加 1 即可。·········
3. FP-Tree還有一樣東西：頭結點表。作用是將所有相同的項鍊接起來，這樣比較容易遍歷。
   最後得到的FP-Tree如下：
   

構造FP-Tree的虛擬碼如下：

演算法：FP-Tree構造演算法
輸入：事務資料集 D，最小支援度閾值 min_sup
輸出：FP-Tree
(1) 　　掃描事務資料集 D 一次，獲得頻繁項的集合 F 和其中每個頻繁項的支援度。對 F 中的所有頻繁項按其支援度進行降序排序，結果為頻繁項表 L ;
(2) 　　建立一個 FP-Tree 的根節點 T，標記為“null”;
(3) 　　for 事務資料集 D 中每個事務 Trans do
(4) 　　　　對 Trans 中的所有頻繁項按照 L 中的次序排序;
(5) 　　　　對排序後的頻繁項表以 [p|P] 格式表示，其中 p 是第一個元素，而 P 是頻繁項表中除去 p 後剩餘元素組成的項表;
(6) 　　　　呼叫函式 insert_tree( [p|P], T );
(7) 　　end for

insert_tree( [p|P], root)
(1) 　　if root 有孩子節點 N and N.item-name=p.item-name then
(2) 　　　　N.count++;
(3) 　　Else
(4) 　　　　建立新節點 N;
(5) 　　　　N.item-name=p.item-name;
(6) 　　　　N.count++;
(7) 　　　　p.parent=root;
(8) 　　　　將 N.node-link 指向樹中與它同專案名的節點;
(9) 　　end if
(10)　　if P 非空 then
(11)　　　　把 P 的第一專案賦值給 p，並把它從 P 中刪除;
(12)　　　　遞迴呼叫 insert_tree( [p|P], N);
(13)　　end if

---

從FP-Tree提取頻繁項集：

相對而言，FP-Tree的構造比較簡單，而從FP-Tree提取頻繁項集比較難理解。其中出現了幾個新名詞，下面直接針對購物籃的FP-Tree進行講解吧。

求以“Ham”為字尾的頻繁項集：

• 根據頭結點表找出“Ham”結尾的路徑：<
  <
  Cola:3, Ham:1>
  >
  和<
  <
  Cola:3, Diaper:2, Beer:2, Ham:1>
  >
  ，代表的意義是：原資料集中(Cola, Ham)和(Cola, Diaper, Beer, Ham)各出現了一次。
• “Ham”的兩個字首路徑{(Cola:1), (Cola Diaper Beer:1)}構成了“Ham”的條件模式基，注意條件模式基的計數都定義為了“Ham”的計數。
• 根據條件模式基構建“Ham”的條件FP-樹：因為在Ham的條件模式基中 Diaper、Beer 只出現了一次，Coal 出現了兩次，所以 Diaper、Beer 是非頻繁項，不包含在Ham的條件FP-樹中。
• “Ham”的條件FP-樹只有一個分支<
  <
  Cola:2>
  >
  ，得到條件頻繁項集 {Cola:2}。
• 條件頻繁項集 {Cola:2} 和字尾模式“Ham”合併，得到頻繁項集 {Cola Ham:2}。

求以“Beer”為字尾的頻繁項集：

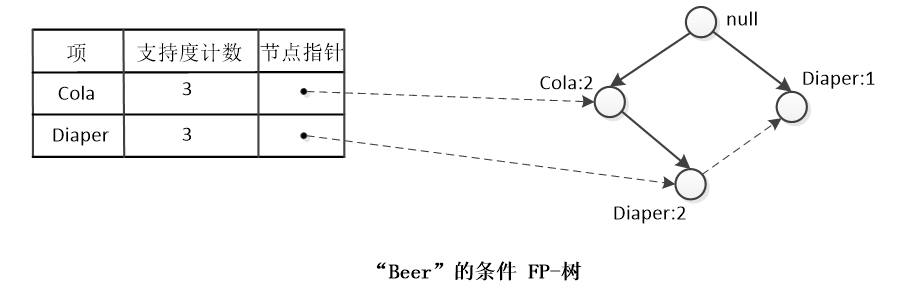
• “Beer”的條件模式基有{(Cola Diaper:2), (Diaper:1)}。
• “Beer”的條件FP-樹如下。
• “Beer”為字尾的頻繁項集為 {Cola Diaper Beer:2}、{Diaper Beer:2}、{Cola Beer:2}
  

求以“Diaper”為字尾的頻繁項集：
　　條件模式基為{(Cola:2)}，最後求得頻繁項集為{Cola Diaper:2}。

綜上，得到的頻繁項集有：{Cola Ham:2}、{Cola Beer:2}、{Diaper Beer:3}、{Cola Diaper:2}、{Cola Diaper Beer:2}。

從FP-Tree提取頻繁項集的主要步驟是：

• 對於每個頻繁項，通過以下步驟求它的條件頻繁項集：
  
  • 找出它的條件模式基
  • 把條件模式基當做事務集去建造一棵樹，這棵樹不叫FP-Tree，而叫做該頻繁項的條件FP-Tree。
  • 對這棵條件FP-Tree遞迴以上操作，即找這棵條件FP-Tree上的子條件頻繁項集。
• 以上找到的都是該頻繁項的條件頻繁項集而已，所以每次遞迴都需要把條件頻繁項集和該頻繁項拼接起來才是我們最終要求的頻繁項集

虛擬碼如下：

演算法：FP-Growth(FP-Tree, α
輸入：已經構造好的 FP-Tree，項集 α

\alpha

（初值為空），最小支援度 min_sup;
輸出：事務資料集 D 中的頻繁項集 L;
(1) 　　L 初值為空
(2) 　　if Tree 只包含單個路徑 P then
(3) 　　　　for 路徑 P 中節點的每個組合（記為 β

\beta

） do
(4) 　　　　　　產生專案集 α∪β

\alpha \cup \beta

，其支援度 support 等於 β

\beta

中節點的最小支援度數;
(5) 　　　　　　return L = L ∪

\cup

支援度數大於 min_sup 的專案集 β∪α

\beta \cup \alpha

(6)　　 else　　　　//包含多個路徑
(7) 　　　　for Tree 的頭表中的每個頻繁項 αf

\alpha_f

do
(8) 　　　　　　產生一個專案集 β

\beta

= αf∪α

\alpha_f \cup \alpha

，其支援度等於 αf

\alpha_f

的支援度;
(9) 　　　　　　構造 β

\beta

的條件模式基 B，並根據該條件模式基 B 構造 β

\beta

的條件 FP- 樹 Treeβ

Tree_{\beta}

;
(10) 　　　　　　if Treeβ≠Φ

Tree_\beta \neq \Phi

then
(11) 　　　　　　　　遞迴呼叫 FP-Growth(Treeβ

Tree_\beta

, β
(12) 　　　　　　end if
(13) 　　　　end for
(14)　　end if

用python語言實現 FP-Growth 的介紹請見：FP_Growth演算法python實現。

轉載請註明出處，謝謝！（原文連結：http://blog.csdn.net/bone_ace/article/details/46669699）