介紹：

樹是資料結構中非常重要的一種，主要的用途是用來提高查詢效率，對於要重複查詢的情況效果更佳，如二叉排序樹、FP-樹。另外可以用來提高編碼效率，如哈弗曼樹。

程式碼：

用python實現樹的構造和幾種遍歷演算法，雖然不難，不過還是把程式碼作了一下整理總結。實現功能：

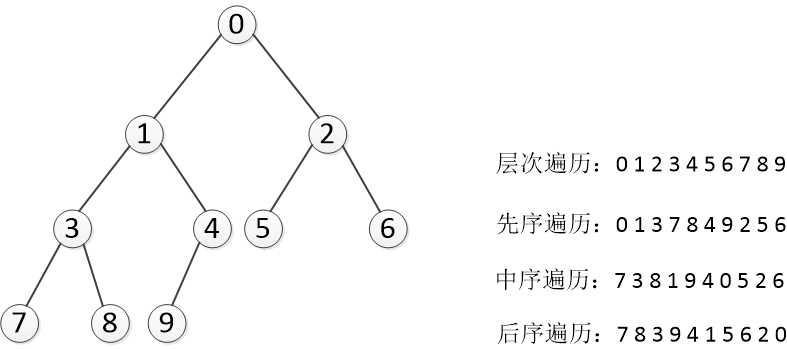
• 樹的構造
• 遞迴實現先序遍歷、中序遍歷、後序遍歷
• 堆疊實現先序遍歷、中序遍歷、後序遍歷
• 佇列實現層次遍歷

#coding=utf-8

class Node(object):
    """節點類"""
    def __init__(self, elem=-1, lchild=None, rchild=None):
        self.elem = elem
        self.lchild = lchild
        self.rchild = rchild


class Tree(object):
    """樹類"""
    def __init__(self):
        self.root = Node()
        self.myQueue = []

    def add(self, elem):
        """為樹新增節點"""
        node = Node(elem)
        if self.root.elem == -1:  # 如果樹是空的，則對根節點賦值
            self.root = node
            self.myQueue.append(self.root)
        else:
            treeNode = self.myQueue[0]  # 此結點的子樹還沒有齊。
            if treeNode.lchild == None:
                treeNode.lchild = node
                self.myQueue.append(treeNode.lchild)
            else:
                treeNode.rchild = node
                self.myQueue.append(treeNode.rchild)
                self.myQueue.pop(0)  # 如果該結點存在右子樹，將此結點丟棄。


    def front_digui(self, root):
        """利用遞迴實現樹的先序遍歷"""
        if root == None:
            return
        print root.elem,
        self.front_digui(root.lchild)
        self.front_digui(root.rchild)


    def middle_digui(self, root):
        """利用遞迴實現樹的中序遍歷"""
        if root == None:
            return
        self.middle_digui(root.lchild)
        print root.elem,
        self.middle_digui(root.rchild)


    def later_digui(self, root):
        """利用遞迴實現樹的後序遍歷"""
        if root == None:
            return
        self.later_digui(root.lchild)
        self.later_digui(root.rchild)
        print root.elem,


    def front_stack(self, root):
        """利用堆疊實現樹的先序遍歷"""
        if root == None:
            return
        myStack = []
        node = root
        while node or myStack:
            while node:                     #從根節點開始，一直找它的左子樹
                print node.elem,
                myStack.append(node)
                node = node.lchild
            node = myStack.pop()            #while結束表示當前節點node為空，即前一個節點沒有左子樹了
            node = node.rchild                  #開始檢視它的右子樹


    def middle_stack(self, root):
        """利用堆疊實現樹的中序遍歷"""
        if root == None:
            return
        myStack = []
        node = root
        while node or myStack:
            while node:                     #從根節點開始，一直找它的左子樹
                myStack.append(node)
                node = node.lchild
            node = myStack.pop()            #while結束表示當前節點node為空，即前一個節點沒有左子樹了
            print node.elem,
            node = node.rchild                  #開始檢視它的右子樹


    def later_stack(self, root):
        """利用堆疊實現樹的後序遍歷"""
        if root == None:
            return
        myStack1 = []
        myStack2 = []
        node = root
        myStack1.append(node)
        while myStack1:                   #這個while迴圈的功能是找出後序遍歷的逆序，存在myStack2裡面
            node = myStack1.pop()
            if node.lchild:
                myStack1.append(node.lchild)
            if node.rchild:
                myStack1.append(node.rchild)
            myStack2.append(node)
        while myStack2:                         #將myStack2中的元素出棧，即為後序遍歷次序
            print myStack2.pop().elem,


    def level_queue(self, root):
        """利用佇列實現樹的層次遍歷"""
        if root == None:
            return
        myQueue = []
        node = root
        myQueue.append(node)
        while myQueue:
            node = myQueue.pop(0)
            print node.elem,
            if node.lchild != None:
                myQueue.append(node.lchild)
            if node.rchild != None:
                myQueue.append(node.rchild)


if __name__ == '__main__':
    """主函式"""
    elems = range(10)           #生成十個資料作為樹節點
    tree = Tree()          #新建一個樹物件
    for elem in elems:                  
        tree.add(elem)           #逐個新增樹的節點

    print '佇列實現層次遍歷:'
    tree.level_queue(tree.root)

    print '\n\n遞迴實現先序遍歷:'
    tree.front_digui(tree.root)
    print '\n遞迴實現中序遍歷:' 
    tree.middle_digui(tree.root)
    print '\n遞迴實現後序遍歷:'
    tree.later_digui(tree.root)

    print '\n\n堆疊實現先序遍歷:'
    tree.front_stack(tree.root)
    print '\n堆疊實現中序遍歷:'
    tree.middle_stack(tree.root)
    print '\n堆疊實現後序遍歷:'
    tree.later_stack(tree.root)

總結：

樹的遍歷主要有兩種，一種是深度優先遍歷，像前序、中序、後序；另一種是廣度優先遍歷，像層次遍歷。在樹結構中兩者的區別還不是非常明顯，但從樹擴充套件到有向圖，到無向圖的時候，深度優先搜尋和廣度優先搜尋的效率和作用還是有很大不同的。
深度優先一般用遞迴，廣度優先一般用佇列。一般情況下能用遞迴實現的演算法大部分也能用堆疊來實現。

我印象中是有遞迴構造樹的方法，卻一直想不出該怎麼構造。後來仔細想了一下，遞迴思想有點類似深度優先演算法，而樹的構造應該是廣度優先的。如果用遞迴的話一定要有個終止條件，例如規定樹深等。不然構造出來的樹會偏向左單子樹或者右單子樹。所以一般樹的構造還是應該用佇列比較好。

以上說的不夠嚴謹，有錯誤之處，歡迎指正！

轉載請註明出處，謝謝！（原文連結：http://blog.csdn.net/bone_ace/article/details/46718683）