跳錶（SkipList）簡介：

給你一個有序陣列，如果現在需要查詢某一個數字，你可能會用二分法。
但是如果給你的是一個有序連結串列，那就用不上二分法了，你能想到什麼方法？
跳錶是一種很好的選擇，理解和實現出來也相對比較容易。

跳錶的查詢：

例如給出連結串列： 30 → 40 → 50 → 60 → 70 → 90
現在要插入一個 80 ，如果是用普通方法從頭到尾逐個搜尋的話需要比較的次數是 6 。但是如果下面的跳錶，則只需要比較 4 次（在元素數量大的時候優勢將會很明顯）：

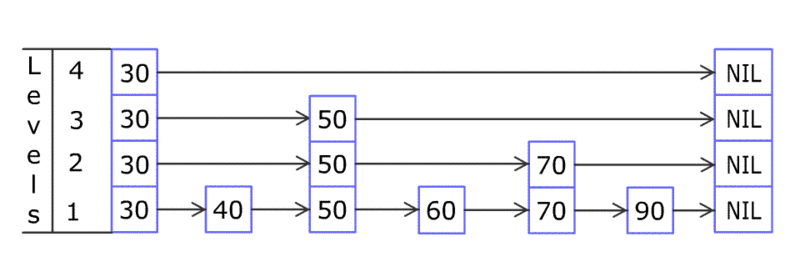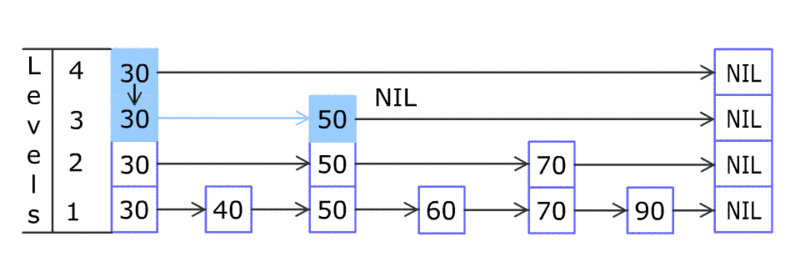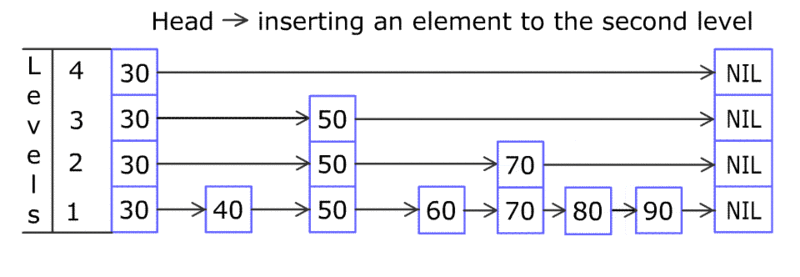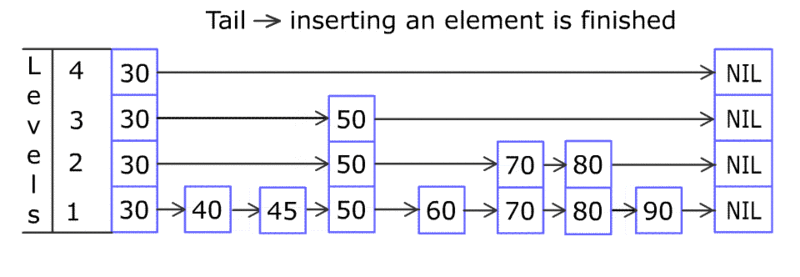
首先認識一下跳錶的結構，以上例子的跳錶有四層，其中最下面一層是完整的連結串列（即包含所有元素）。第 i 層的元素間隔取出，充當“索引”的功能，組成第 i-1 層的元素……

查詢元素的步驟（以80為例）：
首先在第四層比較：80<=30 不成立，第四層比較完畢，進入第三層；
在第三層：80<=50 不成立，第三層比較完畢，進入第二層；
在第二層：80<=70 不成立，第二層比較完畢，進入第一層；
在第一層：80<=90 成立，則找到80的位置，插入即可。

再例如下面的跳錶（-1表示開頭，1表示結尾）：

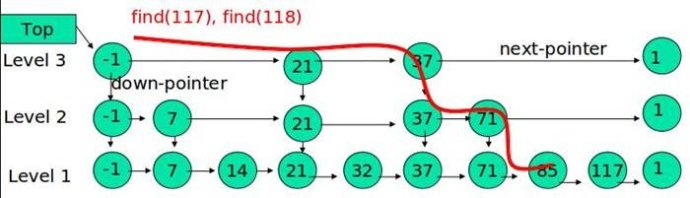
查詢 117 的步驟：
首先在第三層比較：117<=21 不成立，再比較 117<=37 不成立，第三層比較完畢，進入第二層；
在第二層：117<=71 不成立，第二層比較完畢，進入第一層；
在第一層：117<=85不成立，再比較 117<=117 成立，則找到117的位置。

跳錶的插入：

以上步驟已經找到某個元素的位置了，然後在插入某個元素之後還需要考慮是否要將它當做“索引元素”？
例如在第一個例子中：在第一層的連結串列中查詢到並插入80，之後還需要在第二層插入80嗎？第三層呢？到底需要在多少層插入80？

很有意思，這個答案是由一個隨機數決定的，也就是說你還需要新增一個產生隨機數的程式碼，產生一個隨機數來決定到底需要在多少層插入80（一般隨機數的範圍是 [1, 已有層數+1] ）。
但不管插入幾行跳錶都要滿足：如果元素在第 i 層出現了，則一定也出現在 i-1 層。例如對於第一例插入80的情況，如果產生隨機數為2，則一定是在第一層和第二層插入80。

跳錶的刪除：

跳錶的刪除簡單多了，如果要刪除某元素，則所有層的該元素都要刪除。例如對於第一例要刪除50，則第一層、第二層、第三層的 50 都要刪除。

跳錶的核心思想及優點：

很明顯，跳錶主要是利用了“索引”的功能，以空間換時間的思想，使演算法的時間複雜度降低到了 O（logn）！
相對於陣列而言，連結串列最大的優點就是能動態地分配儲存空間、增刪改非常方便，但致命的缺點就在於查詢。
而SkipList的思想簡直就是連結串列的救星，大大縮減了它的缺陷，使連結串列的使用更加廣泛和方便。

參考文獻：《Skip list》、《SkipList跳錶基本原理》。

轉載請註明出處，謝謝！（原文連結：http://blog.csdn.net/bone_ace/article/details/50754242）