Particle Filter Tutorial 粒子濾波：從推導到應用（一）

前言：

     早幾年前寫部落格的時候，編輯公式都是線上網站編輯的，有時候這個網站不穩定，貼的公式看不到。如果有需要，pdf版下載地址點選開啟連結，給您閱讀帶來的不便表示抱歉，祝大家好運。

      博主在自主學習粒子濾波的過程中，看了很多文獻或部落格，不知道是看文獻時粗心大意還是悟性太低，看著那麼多公式，總是無法把握住粒子濾波的思路，也無法將理論和實踐對應起來。比如：理論推導過程中那麼多概率公式，概率怎麼和系統的狀態變數對應上了？狀態粒子是怎麼一步步取樣出來的，為什麼程式裡面都是直接用狀態方程來計算？粒子的權重是怎麼來的？經過一段時間的理解，總算理清了它的脈絡。同時也覺得，只有對理論的推導心中有數了，才能知道什麼樣的地方可以用這個演算法，以及這個演算法有什麼不足。因此，本文將結合實際程式給出粒子濾波的詳細推導，在推導過程中加入博主自己的理解，如有不妥，請指出，謝謝。

     文章架構：

     由最基礎的貝葉斯估計開始介紹，再引出蒙特卡羅取樣，重要性取樣，SIS粒子濾波，重取樣，基本粒子濾波Generic Particle Filter，SIR粒子濾波，這些概念的引進，都是為了解決上一個概念中出現的問題而環環相扣的。最後給出幾個在matlab和python中的應用，例程包括影像跟蹤，濾波，機器人定位。

      再往下看之前，也可以看看《卡爾曼濾波:從推導到應用》，好對這種通過狀態方程來濾波的思路有所瞭解。

一、貝葉斯濾波

      假設有一個系統，我們知道它的狀態方程，和測量方程如下：

        如：       (1)

               如：                                                                  (2)

其中x為系統狀態，y為測量到的資料，f,h是狀態轉移函式和測量函式，v,n為過程噪聲和測量噪聲，噪聲都是獨立同分布的。上面對應的那個例子將會出現在程式中。

      從貝葉斯理論的觀點來看，狀態估計問題（目標跟蹤、訊號濾波）就是根據之前一系列的已有資料（後驗知識）遞推的計算出當前狀態的可信度。這個可信度就是概率公式，它需要通過預測和更新兩個步奏來遞推的計算。

      預測過程是利用系統模型(狀態方程1)預測狀態的先驗概率密度，也就是通過已有的先驗知識對未來的狀態進行猜測，即p( x(k)|x(k-1) )。更新過程則利用最新的測量值對先驗概率密度進行修正，得到後驗概率密度，也就是對之前的猜測進行修正。

     在處理這些問題時，一般都先假設系統的狀態轉移服從一階馬爾科夫模型，即當前時刻的狀態x(k)只與上一個時刻的狀態x(k-1)有關。這是很自然的一種假設，就像小時候玩飛行棋，下一時刻的飛機跳到的位置只由當前時刻的位置和骰子決定。同時，假設k時刻測量到的資料y(k)只與當前的狀態x(k)有關，如上面的狀態方程2。

     為了進行遞推，不妨假設已知k-1時刻的概率密度函式

     預測：由上一時刻的概率密度得到，這個公式的含義是既然有了前面1：k-1時刻的測量資料，那就可以預測一下狀態x(k)出現的概率。

     計算推導如下：

     

                         

                         

等式的第一行到第二行純粹是貝葉斯公式的應用。第二行得到第三行是由於一階馬爾科夫過程的假設，狀態x(k)只由x(k-1)決定。

樓主看到這裡的時候想到兩個問題：

      第一：既然 ，x(k)都只由x(k-1)決定了，即，在這裡弄一個是什麼意思？

      這兩個概率公式含義是不一樣的，前一個是純粹根據模型進行預測，x(k)實實在在的由x(k-1)決定，後一個是既然測到的資料和狀態是有關係的，現在已經有了很多測量資料 y 了，那麼我可以根據已有的經驗對你進行預測，只是猜測x(k)，而不能決定x(k)。

     第二：上面公式的最後一行是假設已知的，但是怎麼得到呢？

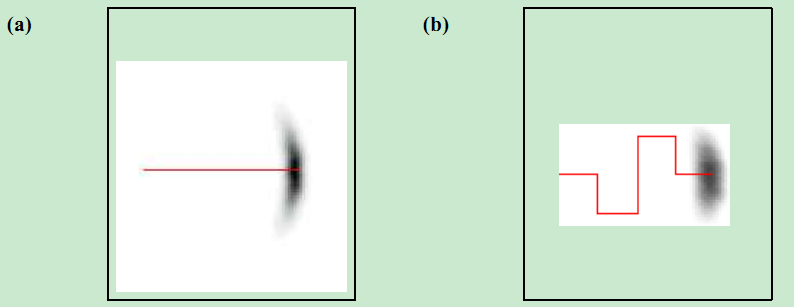
     其實它由系統狀態方程決定，它的概率分佈形狀和系統的過程噪聲形狀一模一樣。如何理解呢?觀察狀態方程(1)式我們知道，x(k) = Constant( x(k-1) ) + v(k-1)  也就是x(k)由一個通過x(k-1)計算出的常數疊加一個噪聲得到。看下面的圖：

如果沒有噪聲，x(k)完全由x(k-1)計算得到，也就沒由概率分佈這個概念了，由於出現了噪聲，所以x(k)不好確定，他的分佈就如同圖中的陰影部分，實際上形狀和噪聲是一樣的，只是進行了一些平移。理解了這一點，對粒子濾波程式中，狀態x(k)的取樣的計算很有幫助，要取樣x(k)，直接取樣一個過程噪聲，再疊加上 f(x(k-1)) 這個常數就行了。

     更新：由得到後驗概率。這個後驗概率才是真正有用的東西，上一步還只是預測，這裡又多了k時刻的測量，對上面的預測再進行修正，就是濾波了。這裡的後驗概率也將是代入到下次的預測，形成遞推。

     推導：

     

                              

其中歸一化常數：

      

等式第一行到第二行是因為測量方程知道, y(k)只與x(k)有關，也稱之為似然函式，由量測方程決定。也和上面的推理一樣，, x(k)部分是常數，也是隻和量測噪聲n(k)的概率分佈有關，注意這個也將為SIR粒子濾波里權重的取樣提供程式設計依據。

       貝葉斯濾波到這裡就告一段落了。但是，請注意上面的推導過程中需要用到積分，這對於一般的非線性，非高斯系統，很難得到後驗概率的解析解。為了解決這個問題，就得引進蒙特卡洛取樣。關於它的具體推導請見 下一篇博文。

（轉載請註明作者和出處：http://blog.csdn.net/heyijia0327 未經允許請勿用於商業用途）

reference：

1.M. Sanjeev Arulampalam 《A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking》

2.ZHE CHEN 《Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond》

3.Sebastian THRUN 《Probabilistic Robotics》

3.百度文庫 《粒子濾波理論》