c#擴充套件方法奇思妙用變態篇一：由Fibonacci數列引出“委託擴充套件”及“遞推遞迴委託”

先回顧一個數列的概念：按一定次序排列的一列 數 稱為數列...(請參見百度百科：數列)
幾個簡單的數列：
      1, 1, 1, 1, 1, 1, 1...                //數列1
      0, 1, 2, 3, 4, 5, 6, 7...                //數列2
      0, 1, 4, 9, 16, 25, 36, 49...        //數列3
通項公式的定義：數列的第n項與項的序數這間的關係，也就是數列生成演算法
上面幾個數列可表示為
       An = F(n) = 1
       An = F(n) = n
       An = F(n) = n * n

有了數列和通項公式的定義，我們的任務就好描述了：
      用最簡潔的程式碼描述通項公式，用最簡潔演算法生成數列的前N個數。

在此要求下，用常規程式碼是做不到簡潔的，這裡我們用lambda表示式描述通項公式：

lambda表示式是不是與數學公式很像啊！

再來看生成演算法，這裡用了一個不一般的擴充套件：

        /// 

        /// 生成佇列的前count項
        /// 
        /// 通項公式
        /// 生成的數量
        /// 佇列前count項
        public static IEnumerable<int> GetSequence(this Func<int, int> func, int count)
        {
            for (int i = 0; i < count; i++) yield return func(i);
        }

相信大家見的擴充套件大多針對類(object, string)、介面(IEnumerable)進行擴充套件，針對Func（委託）估計對大多數人來說都是第一次。
這個擴充套件就是標題中說的“委託擴充套件”，感覺很怪吧，很彆扭吧，很別管太多，看看怎麼呼叫吧：

        public static void Test1()
        {
            int[] ints1 = fun1.GetSequence(10).ToArray();      //1, 1, 1, 1
            int[] ints2 = fun2.GetSequence(10).ToArray();      //0, 1, 2, 3
            int[] ints3 = fun3.GetSequence(10).ToArray(); ;    //0, 1, 4, 9
        }

自我感覺比較簡潔，而且將生成數列（GetSequence）與數列演算法(通項公式)分開，也達到了生成數列（GetSequence）的複用。

上面幾個數列比較簡單，現在來看Fibonacci，
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
用圖形表示如下：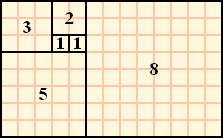

這個序列在大家學習c語言遞推遞迴時都接觸過，這個序列很神奇，請參看維基百科：斐波那契數列
它的通項公式是 An = F(n) = n                          n =0, 1
                                       F(n-1) + F(n-2)      n>1
注意：關於這數列有的是從n從0開始，有的是從1開始，這裡不計較。

遞推遞迴演算法如下，容易理解效率確很低！！

本文是為了引出遞推遞迴委託，暫不是演算法的效率
下面就要大（改）變（形）態了。

不考慮 <1 的情況

與數學通項式對比一下，何其相似！這就是我們的“遞推遞迴委託”！

考慮所有情況，完成Fibonacci，如下

實在感嘆c#精簡的語法，一句程式碼可以表示一個遞推遞迴！
呼叫測試下吧！

當然這個生成演算法效率不是一般的低！

最後給出一個數學推匯出的精確演算法

一點意見：像這樣程式碼，最好是給封裝起來，否則會很麻煩的。
這篇文章是給極少數人看的（啟發一下），看完後封裝好給大多數人用。這是也“變態篇”系列文章的宗旨.
希望大家對 “委託擴充套件” 和 “遞推遞迴委託”提些看法，名字定義不太好，請指正！