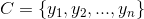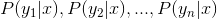抽象的藝術-樸素貝葉斯

浩哥001發表於2017-03-08
抽象

Situation

2016年，A市對30000+市民進行了年收入統計，收入>=50K的人數7000+，<=50K的人數20000+。

為了提高稅收，需要分析兩種收入群體的特徵，分析員抽取了“職業、年齡、性別、出生地、教育程度”等屬性，更進一步分析哪些職業收入高，哪個年齡段收入高等等，為來年稅收做預測。

問題來了：2017年2月，A市人口增加了20000+，對這個群體年收入做預測。

樸素貝葉斯

分類演算法有很多種，今天講樸素貝葉斯的原理和Java實現。

樸素貝葉斯分類的正式定義如下：

  • 設為一個待分類樣本x，而每個a為x的一個特徵屬性。

    • screenshot.png

  • 分類集合。

    • screenshot.png

  • 計算分類樣本x的分類概率。

    • screenshot.png

  • 求樣本x的分類概率max。

    • screenshot.png

要解決上面提到的問題，對新的人口樣本做年收入預測，一般的步驟如下（適合入門的同學）：

  • 歷史樣本準備。
  • 訓練，輸出模型。
  • 測試，輸出測試結果。
  • 評估，評估測試結果，預測模型是否足夠準確。
  • 應用。

接下來上程式碼：

樣本

public class Sample {
    //分類
    private String label;
    //屬性
    private List<Attribute> attributes;

    public Sample(String label, List<Attribute> attributes) {
        this.label = label;
        this.attributes = attributes;
    }

    public Integer getId() {
        return hashCode();
    }

    public String getLabel() {
        return label;
    }

    public List<Attribute> getAttributes() {
        return attributes;
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;

        Sample sample = (Sample) o;

        if (!attributes.equals(sample.attributes)) return false;
        if (!label.equals(sample.label)) return false;

        return true;
    }

    @Override
    public int hashCode() {
        int result = label.hashCode();
        result = 31 * result + attributes.hashCode();
        return result;
    }
}

屬性

public class Attribute {
    private String field;
    private String value;

    public Attribute(String field, String value) {
        this.field = field;
        this.value = value;
    }

    public String getField() {
        return field;
    }

    public String getValue() {
        return value;
    }
}

訓練

  • train
   /**
     * 訓練
     */
    public void train() {
        calClassesPrior();
        calFeatureClassPrior();
    }
  • 分類的先驗概率
   /**
     * 計算分類先驗概率
     */
    private synchronized void calClassesPrior() {
        for (Sample sample : trainingDataSet) {
            String label = sample.getLabel();
            Double labelCount = classCount.get(label);
            if (labelCount == null) {
                classCount.put(label, 1.0);
            } else {
                classCount.put(label, ++labelCount);
            }
        }
        Double total = new Double(trainingDataSet.size());
        for (Map.Entry<String, Double> entry : classCount.entrySet()) {
            Double prob = entry.getValue() / total.doubleValue();
            classPrior.put(entry.getKey(), prob);
        }
    }
  • 特徵在各分類的先驗概率
   /**
     * 計算feature class的先驗概率
     */
    private synchronized void calFeatureClassPrior() {
        Map<String, Double> featureClassCounts = new HashMap<String, Double>();
        for (Sample sample : trainingDataSet) {
            String label = sample.getLabel();
            for (Attribute attribute : sample.getAttributes()) {
                String attName = attribute.getField();
                String attValue = attribute.getValue();
                //feature class key
                String fc = String.format(FEATURE_CLASS_FORMAT, attName, attValue, label);
                Double fcCount = featureClassCounts.get(fc);
                if (fcCount == null) {
                    featureClassCounts.put(fc, 1.0);
                } else {
                    featureClassCounts.put(fc, ++fcCount);
                }
            }
        }

        //輸出模型
        for (Map.Entry<String, Double> entry : featureClassCounts.entrySet()) {
            String label = entry.getKey().split("_")[2];
            Double prob = (entry.getValue() / classCount.get(label)) * getClassPrior(label);
            featureClassProb.put(entry.getKey(), prob);
            System.out.printf("f|c: %s, fc count: %f, class count: %f , P(f|c): %.12f 
", entry.getKey(), entry.getValue(), classCount.get(label), featureClassProb.get(entry.getKey()));
        }
    }
  • 屬性特徵分類概率
f|c: a8_ 2635_ <=50K, fc count: 11.000000, class count: 24720.000000 , P(f|c): 0.000337827462 
f|c: a10_ 63_ <=50K, fc count: 7.000000, class count: 24720.000000 , P(f|c): 0.000214981112 
f|c: a9_ 1668_ <=50K, fc count: 4.000000, class count: 24720.000000 , P(f|c): 0.000122846350 
f|c: a8_ 7896_ >50K, fc count: 3.000000, class count: 7841.000000 , P(f|c): 0.000092134762 
f|c: a9_ 2489_ <=50K, fc count: 1.000000, class count: 24720.000000 , P(f|c): 0.000030711587 
f|c: a10_ 65_ >50K, fc count: 104.000000, class count: 7841.000000 , P(f|c): 0.003194005098 
f|c: a10_ 74_ <=50K, fc count: 1.000000, class count: 24720.000000 , P(f|c): 0.000030711587 
f|c: a8_ 4865_ <=50K, fc count: 17.000000, class count: 24720.000000 , P(f|c): 0.000522096987 
f|c: a10_ 7_ >50K, fc count: 4.000000, class count: 7841.000000 , P(f|c): 0.000122846350 
f|c: a10_ 70_ >50K, fc count: 106.000000, class count: 7841.000000 , P(f|c): 0.003255428273 
f|c: a11_ Yugoslavia_ <=50K, fc count: 10.000000, class count: 24720.000000 , P(f|c): 0.000307115875 
f|c: a9_ 1902_ <=50K, fc count: 13.000000, class count: 24720.000000 , P(f|c): 0.000399250637 
f|c: a2_ 2_ <=50K, fc count: 162.000000, class count: 24720.000000 , P(f|c): 0.004975277172 
f|c: a10_ 30_ <=50K, fc count: 1066.000000, class count: 24720.000000 , P(f|c): 0.032738552256 
f|c: a8_ 3674_ <=50K, fc count: 14.000000, class count: 24720.000000 , P(f|c): 0.000429962225 
f|c: a8_ 34095_ <=50K, fc count: 5.000000, class count: 24720.000000 , P(f|c): 0.000153557937 
f|c: a10_ 13_ >50K, fc count: 2.000000, class count: 7841.000000 , P(f|c): 0.000061423175 
f|c: a11_ Thailand_ >50K, fc count: 3.000000, class count: 7841.000000 , P(f|c): 0.000092134762 
f|c: a10_ 41_ <=50K, fc count: 29.000000, class count: 24720.000000 , P(f|c): 0.000890636037

分類

/**
     * 分類
     *
     * @param sample
     * @return
     */
    public String classify(Sample sample) {
        String clazz = "";
        Double clazzProb = 0.0;
        for (Map.Entry<String, Double> classProb : classPrior.entrySet()) {
            String label = classProb.getKey();
            Double prob = classProb.getValue();
            for (Attribute attribute : sample.getAttributes()) {
                prob *= getFeatureProb(attribute.getField(), attribute.getValue(), label);
            }

            if (prob > clazzProb) {
                clazz = label;
                clazzProb = prob;
            }

        }
        System.out.printf("probability: %.12f ,class pre: %s, class fact: %s 
", clazzProb, clazz, sample.getLabel());
        return clazz;
    }

測試

抽樣100條測試資料進行分類

probability: 0.000001088450 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000000053 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000918274 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000000002 ,class pre:  >50K, class fact:  >50K. 
probability: 0.000000016812 ,class pre:  <=50K, class fact:  >50K. 
probability: 0.000000002483 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000003344 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000012379 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000485467 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000262052 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000000000024 ,class pre:  <=50K, class fact:  >50K. 
probability: 0.000005353829 ,class pre:  <=50K, class fact:  <=50K. 
probability: 0.000004912284 ,class pre:  <=50K, class fact:  >50K. 
total: 100 correct: 84

gitlab原始碼

內網：gitlab/我的域賬號/algorithm

後記

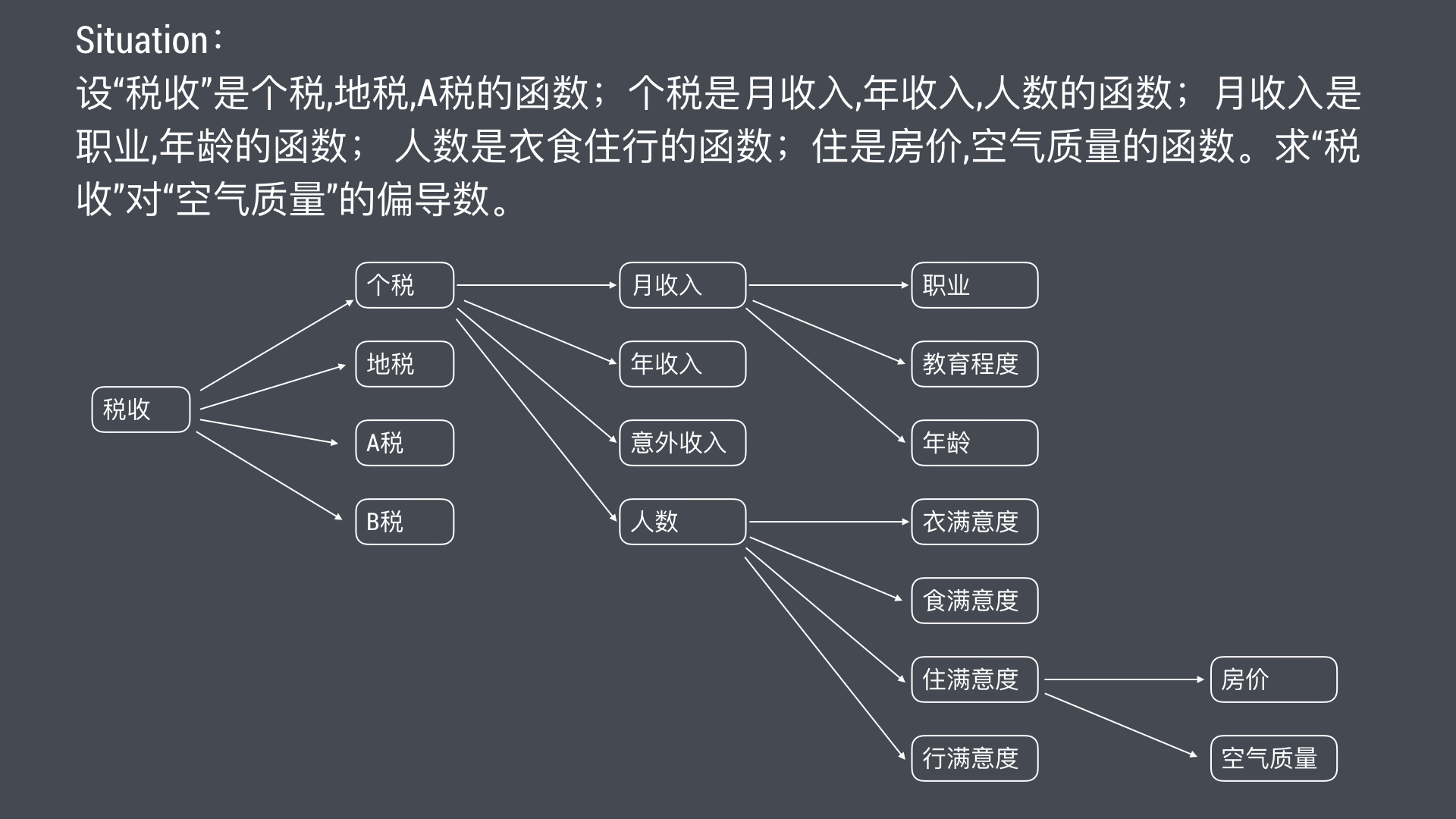
2017年，A市對40000+市民進行了居住滿意度調研，衣食住行，結果市民對環境很不滿意。
問題：改善環境對稅收的收益。

智慧預測.001.jpeg


相關文章