一個例子

高斯混合模型（Gaussian Mixed Model）指的是多個高斯分佈函式的線性組合，理論上GMM可以擬合出任意型別的分佈，通常用於解決同一集合下的資料包含多個不同的分佈的情況（或者是同一類分佈但引數不一樣，或者是不同型別的分佈，比如正態分佈和伯努利分佈）。

如圖1，圖中的點在我們看來明顯分成兩個聚類。這兩個聚類中的點分別通過兩個不同的正態分佈隨機生成而來。但是如果沒有GMM，那麼只能用一個的二維高斯分佈來描述圖1中的資料。圖1中的橢圓即為二倍標準差的正態分佈橢圓。這顯然不太合理，畢竟肉眼一看就覺得應該把它們分成兩類。

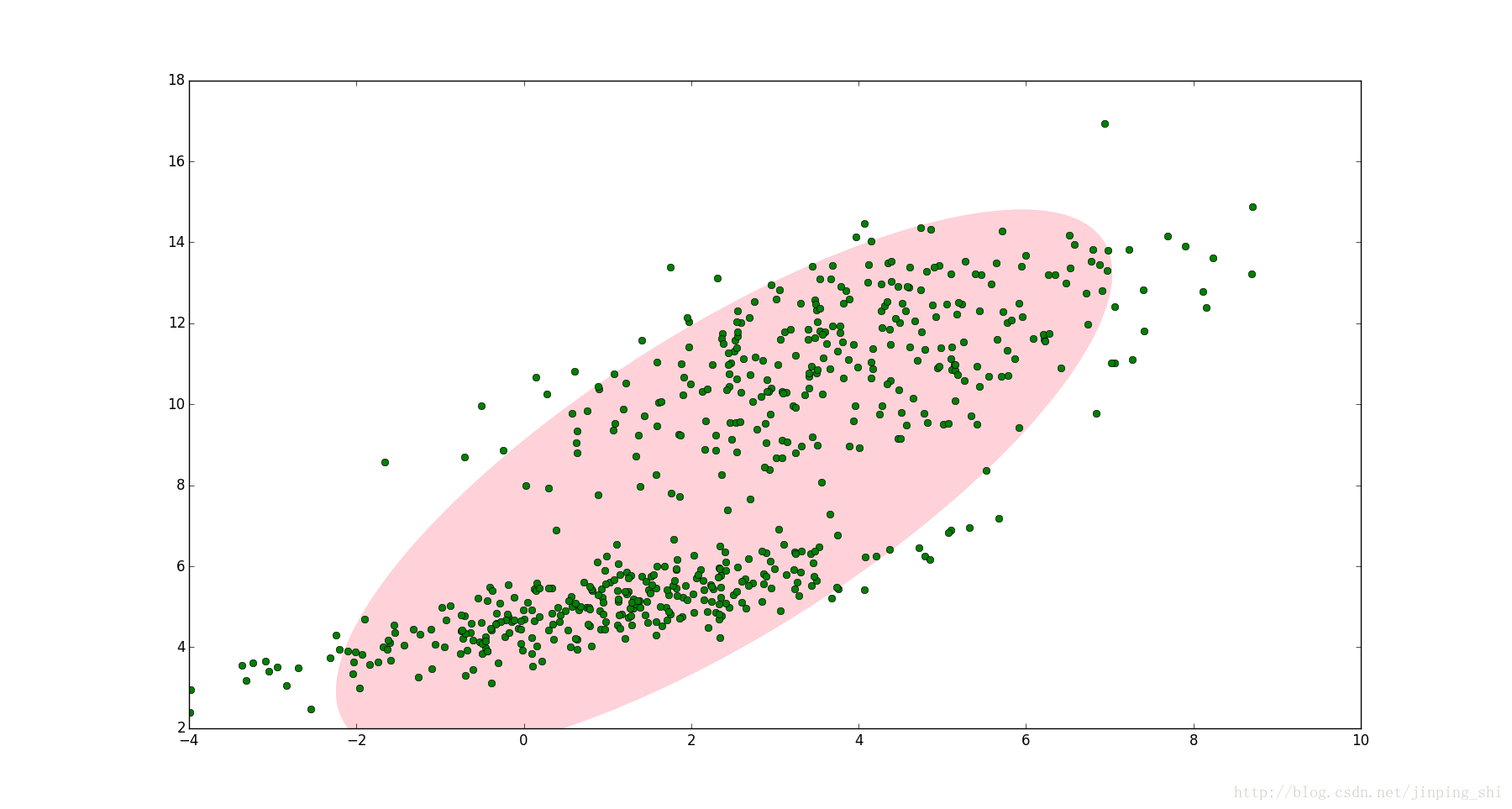
圖1

這時候就可以使用GMM了！如圖2，資料在平面上的空間分佈和圖1一樣，這時使用兩個二維高斯分佈來描述圖2中的資料，分別記為$\mathcal{N}(\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1)$和$\mathcal{N}(\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)$. 圖中的兩個橢圓分別是這兩個高斯分佈的二倍標準差橢圓。可以看到使用兩個二維高斯分佈來描述圖中的資料顯然更合理。實際上圖中的兩個聚類的中的點是通過兩個不同的正態分佈隨機生成而來。如果將兩個二維高斯分佈$\mathcal{N}(\boldsymbol{\mu_1}, \boldsymbol{\Sigma}_1)$和$\mathcal{N}(\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)$合成一個二維的分佈，那麼就可以用合成後的分佈來描述圖2中的所有點。最直觀的方法就是對這兩個二維高斯分佈做線性組合，用線性組合後的分佈來描述整個集合中的資料。這就是高斯混合模型（GMM）。

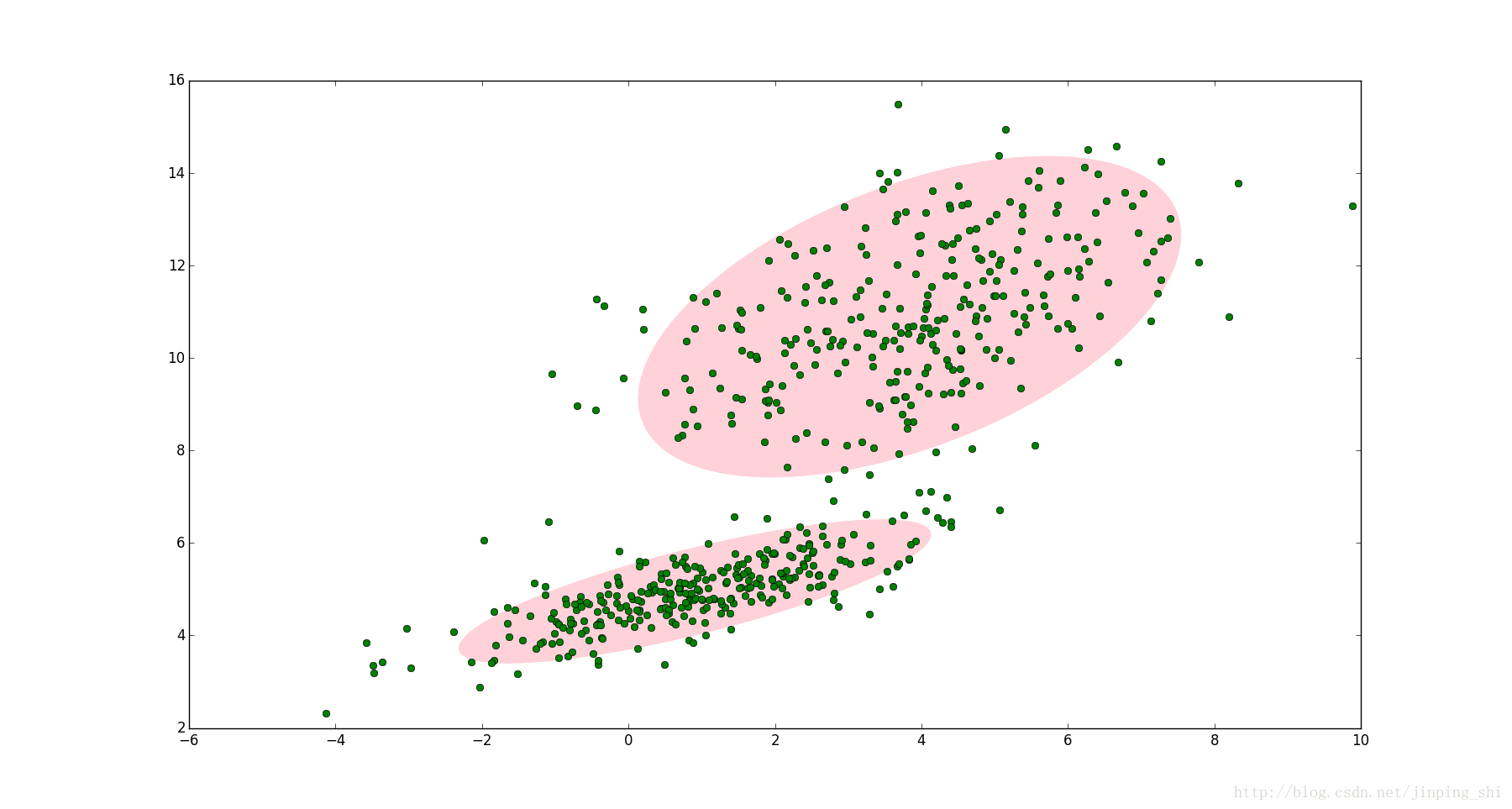
圖2

高斯混合模型（GMM）

設有隨機變數$\boldsymbol{X}$，則混合高斯模型可以用下式表示：
$p(\boldsymbol{x}) = \sum_{k=1}^K\pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$

其中$\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$稱為混合模型中的第$k$個分量（component）。如前面圖2中的例子，有兩個聚類，可以用兩個二維高斯分佈來表示，那麼分量數$K = 2$. $\pi_k$是混合係數（mixture coefficient），且滿足：
$\sum_{k=1}^K\pi_k = 1$
$0 \leq \pi_k \leq 1$

實際上，可以認為$\pi_k$就是每個分量$\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$的權重。

GMM的應用

GMM常用於聚類。如果要從 GMM 的分佈中隨機地取一個點的話，實際上可以分為兩步：首先隨機地在這 K 個 Component 之中選一個，每個 Component 被選中的概率實際上就是它的係數$\pi_k$ ，選中 Component 之後，再單獨地考慮從這個 Component 的分佈中選取一個點就可以了──這裡已經回到了普通的 Gaussian 分佈，轉化為已知的問題。

將GMM用於聚類時，假設資料服從混合高斯分佈（Mixture Gaussian Distribution），那麼只要根據資料推出 GMM 的概率分佈來就可以了；然後 GMM 的 K 個 Component 實際上對應$K$個 cluster 。根據資料來推算概率密度通常被稱作 density estimation 。特別地，當我已知（或假定）概率密度函式的形式，而要估計其中的引數的過程被稱作『引數估計』。

例如圖2的例子，很明顯有兩個聚類，可以定義$K=2$. 那麼對應的GMM形式如下：
$p(\boldsymbol{x}) =\pi_1 \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1) + \pi_2 \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)$

上式中未知的引數有六個：$(\pi_1, \boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1; \pi_2, \boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)$. 之前提到GMM聚類時分為兩步，第一步是隨機地在這$K$個分量中選一個，每個分量被選中的概率即為混合係數$\pi_k$. 可以設定$\pi_1 = \pi_2 = 0.5$，表示每個分量被選中的概率是0.5，即從中抽出一個點，這個點屬於第一類的概率和第二類的概率各佔一半。但實際應用中事先指定$\pi_k$的值是很笨的做法，當問題一般化後，會出現一個問題：當從圖2中的集合隨機選取一個點，怎麼知道這個點是來自$N(\boldsymbol{x}|\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1)$還是$N(\boldsymbol{x}|\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)$呢？換言之怎麼根據資料自動確定$\pi_1$和$\pi_2$的值？這就是GMM引數估計的問題。要解決這個問題，可以使用EM演算法。通過EM演算法，我們可以迭代計算出GMM中的引數：$(\pi_k, \boldsymbol{x}_k, \boldsymbol{\Sigma}_k)$.

GMM引數估計過程

GMM的貝葉斯理解

在介紹GMM引數估計之前，先改寫GMM的形式，改寫之後的GMM模型可以方便地使用EM估計引數。GMM的原始形式如下：

$p(\boldsymbol{x}) = \sum_{k=1}^K\pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \tag{1}$

前面提到$\pi_k$可以看成是第$k$類被選中的概率。我們引入一個新的$K$維隨機變數$\boldsymbol{z}$. $z_k (1 \leq k \leq K)$只能取0或1兩個值；$z_k = 1$表示第$k$類被選中的概率，即：$p(z_k = 1) = \pi_k$；如果$z_k = 0$表示第$k$類沒有被選中的概率。更數學化一點，$z_k$要滿足以下兩個條件：
$z_k \in \{0,1\}$
$\sum_K z_k = 1$

例如圖2中的例子，有兩類，則$\boldsymbol{z}$的維數是2. 如果從第一類中取出一個點，則$\boldsymbol{z} = (1, 0)$；，如果從第二類中取出一個點，則$\boldsymbol{z} = (0, 1)$.

$z_k=1$的概率就是$\pi_k$，假設$z_k$之間是獨立同分布的（iid），我們可以寫出$\boldsymbol{z}$的聯合概率分佈形式，就是連乘：

$p(\boldsymbol{z}) = p(z_1) p(z_2)...p(z_K) = \prod_{k=1}^K \pi_k^{z_k} \tag{2}$

因為$z_k$只能取0或1，且$\boldsymbol{z}$中只能有一個$z_k$為1而其它$z_j (j\neq k)$全為0，所以上式是成立的。

圖2中的資料可以分為兩類，顯然，每一類中的資料都是服從正態分佈的。這個敘述可以用條件概率來表示：
$p(\boldsymbol{x}|z_k = 1) = \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$
即第$k$類中的資料服從正態分佈。進而上式有可以寫成如下形式：
$p(\boldsymbol{x}| \boldsymbol{z}) = \prod_{k=1}^K \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)^{z_k} \tag{3}$

上面分別給出了$p(\boldsymbol{z})$和$p(\boldsymbol{x}| \boldsymbol{z})$的形式，根據條件概率公式，可以求出$p(\boldsymbol{x})$的形式：

$\begin{aligned} p(\boldsymbol{x}) &= \sum_{\boldsymbol{z}} p(\boldsymbol{z}) p(\boldsymbol{x}| \boldsymbol{z}) \\ &= \sum_{\boldsymbol{z}} \left(\prod_{k=1}^K \pi_k^{z_k} \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)^{z_k} \right ) \\ &= \sum_{k=1}^K \pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \end{aligned} \tag{4}$

（注：上式第二個等號，對$\boldsymbol{z}$求和，實際上就是$\sum_{k=1}^K$。又因為對某個$k$，只要$i \ne k$，則有$z_i = 0$，所以$z_k=0$的項為1，可省略，最終得到第三個等號）

可以看到GMM模型的(1)式與(4)式有一樣的形式，且(4)式中引入了一個新的變數$\boldsymbol{z}$，通常稱為隱含變數（latent variable）。對於圖2中的資料，『隱含』的意義是：我們知道資料可以分成兩類，但是隨機抽取一個資料點，我們不知道這個資料點屬於第一類還是第二類，它的歸屬我們觀察不到，因此引入一個隱含變數$\boldsymbol{z}$來描述這個現象。

注意到在貝葉斯的思想下，$p(\boldsymbol{z})$是先驗概率， $p(\boldsymbol{x}| \boldsymbol{z})$是似然概率，很自然我們會想到求出後驗概率$p(\boldsymbol{z}| \boldsymbol{x})$：
$\begin{aligned} \gamma(z_k) &= p(z_k = 1| \boldsymbol{x}) \\ &= \frac{p(z_k = 1) p(\boldsymbol{x}|z_k = 1)}{p(\boldsymbol{x}, z_k = 1)} \\ &= \frac{p(z_k = 1) p(\boldsymbol{x}|z_k = 1)}{\sum_{j=1}^K p(z_j = 1) p(\boldsymbol{x}|z_j = 1)} \\ &= \frac{\pi_k \mathcal{N}(\boldsymbol{x|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k})}{\sum_{j=1}^K \pi_j \mathcal{N}(\boldsymbol{x|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j})} \end{aligned} \tag{5}$

（第2行，貝葉斯定理。關於這一行的分母，很多人有疑問，應該是$p(\boldsymbol{x}, z_k = 1)$還是$p(\boldsymbol{x})$，按照正常寫法，應該是$p(\boldsymbol{x})$。但是為了強調$z_k$的取值，有的書會寫成$p(\boldsymbol{x}, z_k = 1)$，比如李航的《統計學習方法》，這裡就約定$p(\boldsymbol{x})$與$p(\boldsymbol{x}, z_k = 1)$是等同的）
（第3行，全概率公式)
（最後一個等號，結合(3)(4)）

上式中我們定義符號$\gamma(z_k)$來表示來表示第$k$個分量的後驗概率。在貝葉斯的觀點下，$\pi_k$可視為$z_k=1$的先驗概率。

上述內容改寫了GMM的形式，並引入了隱含變數$\boldsymbol{z}$和已知${\boldsymbol{x}}$後的的後驗概率$\gamma(z_k)$，這樣做是為了方便使用EM演算法來估計GMM的引數。

EM演算法估計GMM引數

EM演算法（Expectation-Maximization algorithm）分兩步，第一步先求出要估計引數的粗略值，第二步使用第一步的值最大化似然函式。因此要先求出GMM的似然函式。

假設$\boldsymbol{x} = \{\boldsymbol{x}_1, \boldsymbol{x}_2, ..., \boldsymbol{x}_N\}$，對於圖2，$\boldsymbol{x}$是圖中所有點（每個點有在二維平面上有兩個座標，是二維向量，因此$\boldsymbol{x}_1, \boldsymbol{x}_2$等都用粗體表示）。GMM的概率模型如(1)式所示。GMM模型中有三個引數需要估計，分別是$\boldsymbol{\pi}$，$\boldsymbol{\mu}$和$\boldsymbol{\Sigma}$. 將(1)式稍微改寫一下：
$p(\boldsymbol{x}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{k=1}^K\pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \tag{6}$

為了估計這三個引數，需要分別求解出這三個引數的最大似然函式。先求解$\mu_k$的最大似然函式。樣本符合iid，(6)式所有樣本連乘得到最大似然函式，對(6)式取對數得到對數似然函式，然後再對$\boldsymbol{\mu_k}$求導並令導數為0即得到最大似然函式。
$0 = -\sum_{n=1}^N \frac{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\sum_j \pi_j \mathcal{N}(\boldsymbol{x}_n|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)} \boldsymbol{\Sigma}_k (\boldsymbol{x}_n - \boldsymbol{\mu}_k) \tag{7}$

注意到上式中分數的一項的形式正好是(5)式後驗概率的形式。兩邊同乘$\boldsymbol{\Sigma}_k^{-1}$，重新整理可以得到：
$\boldsymbol{\mu}_k = \frac{1}{N_k}\sum_{n=1}^N \gamma(z_{nk}) \boldsymbol{x}_n \tag{8}$

其中：
$N_k = \sum_{n=1}^N \gamma(z_{nk}) \tag{9}$

(8)式和(9)式中，$N$表示點的數量。$\gamma(z_{nk})$表示點$n$（$\boldsymbol{x}_n$）屬於聚類$k$的後驗概率。則$N_k$可以表示屬於第$k$個聚類的點的數量。那麼$\boldsymbol{\mu}_k$表示所有點的加權平均，每個點的權值是$\sum_{n=1}^N \gamma(z_{nk})$，跟第$k$個聚類有關。

同理求$\boldsymbol{\Sigma}_k$的最大似然函式，可以得到：
$\boldsymbol{\Sigma}_k = \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk}) (x_n - \boldsymbol{\mu}_k)(x_n - \boldsymbol{\mu}_k)^T \tag{10}$

最後剩下$\pi_k$的最大似然函式。注意到$\pi_k$有限制條件$\sum_{k=1}^K\pi_k = 1$，因此我們需要加入拉格朗日運算元：
$\ln p(\boldsymbol{x}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) + \lambda(\sum_{k=1}^K \pi_k -1)$

求上式關於$\pi_k$的最大似然函式，得到：
$0 = \sum_{n=1}^N \frac{\mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\sum_j \pi_j \mathcal{N}(\boldsymbol{x}_n|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)} + \lambda \tag{11}$

上式兩邊同乘$\pi_k$，我們可以做如下推導：

$0 = \sum_{n=1}^N \frac{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\sum_j \pi_j \mathcal{N}(\boldsymbol{x}_n|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)} + \lambda \pi_k \tag{11.1}$

結合公式(5)、(9)，可以將上式改寫成：

$0 = N_k + \lambda \pi_k \tag{11.2}$

注意到$\sum_{k=1}^K \pi_k = 1$，上式兩邊同時對$k$求和。此外$N_k$表示屬於第個聚類的點的數量（公式(9)）。對$N_k，$從$k=1$到$k=K$求和後，就是所有點的數量$N$:

$0 = \sum_{k=1}^K N_k + \lambda \sum_{k=1}^K \pi_k \tag{11.3}$

$0 = N + \lambda \tag{11.4}$

從而可得到$\lambda = -N$，帶入(11.2)，進而可以得到$\pi_k$更簡潔的表示式：
$\pi_k = \frac{N_k}{N} \tag{12}$

EM演算法估計GMM引數即最大化(8)，(10)和(12)。需要用到(5)，(8)，(10)和(12)四個公式。我們先指定$\boldsymbol{\pi}$，$\boldsymbol{\mu}$和$\boldsymbol{\Sigma}$的初始值，帶入(5)中計算出$\gamma(z_{nk})$，然後再將$\gamma(z_{nk})$帶入(8)，(10)和(12)，求得$\pi_k$，$\boldsymbol{\mu}_k$和$\boldsymbol{\Sigma}_k$；接著用求得的$\pi_k$，$\boldsymbol{\mu}_k$和$\boldsymbol{\Sigma}_k$再帶入(5)得到新的$\gamma(z_{nk})$，再將更新後的$\gamma(z_{nk})$帶入(8)，(10)和(12)，如此往復，直到演算法收斂。

EM演算法

1. 定義分量數目$K$，對每個分量$k$設定$\pi_k$，$\boldsymbol{\mu}_k$和$\boldsymbol{\Sigma}_k$的初始值，然後計算(6)式的對數似然函式。
2. E step
   根據當前的$\pi_k$、$\boldsymbol{\mu}_k$、$\boldsymbol{\Sigma}_k$計算後驗概率$\gamma(z_{nk})$
   $\gamma(z_{nk}) = \frac{\pi_k\mathcal{N}(\boldsymbol{x}_n| \boldsymbol{\mu}_n, \boldsymbol{\Sigma}_n)}{\sum_{j=1}^K \pi_j \mathcal{N}(\boldsymbol{x}_n| \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}$
3. M step
   根據E step中計算的$\gamma(z_{nk})$再計算新的$\pi_k$、$\boldsymbol{\mu}_k$、$\boldsymbol{\Sigma}_k$
   $\begin{aligned} \boldsymbol{\mu}_k^{new} &= \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk}) \boldsymbol{x}_n \\ \boldsymbol{\Sigma}_k^{new} &= \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk}) (\boldsymbol{x}_n - \boldsymbol{\mu}_k^{new}) (\boldsymbol{x}_n - \boldsymbol{\mu}_k^{new})^T \\ \pi_k^{new} &= \frac{N_k}{N} \end{aligned}$
   其中：
   $N_k = \sum_{n=1}^N \gamma(z_{nk})$
4. 計算(6)式的對數似然函式
   $\ln p(\boldsymbol{x}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{n=1}^N \ln \left\{\sum_{k=1}^K \pi_k \mathcal{N}(\boldsymbol{x}_k| \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\right\}$
5. 檢查引數是否收斂或對數似然函式是否收斂，若不收斂，則返回第2步。

Reference

1. 漫談 Clustering (3): Gaussian Mixture Model
2. Draw Gaussian distribution ellipse
3. Pang-Ning Tan 等, 資料探勘導論（英文版）, 機械工業出版社, 2010
4. Christopher M. Bishop etc., Pattern Recognition and Machine Learning, Springer, 2006
5. 李航, 統計學習方法, 清華大學出版社, 2012