堆排序演算法

在瞭解堆排序演算法的原理之前，我們必須先來了解一下什麼是堆？堆就是一個近似的完全的二叉樹。那什麼又是完全二叉樹呢？完全二叉樹的定義如下：

　　若設二叉樹的高度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第 h 層從右向左連續缺若干結點，這就是完全二叉樹。完全二叉樹的圖示如下：

　　由上面這幅圖可看出完全二叉樹的特點：最後一層從左向右連續缺失節點。

　　堆就是將陣列表示為完全二叉樹的形式，那麼如何把陣列轉換成堆呢？接下來以一個圖演示陣列轉換成堆。假設有一個整型陣列：｛5，4，8，3，2，1｝

  瞭解完堆的概念之後，我們還需要知道大根堆：大根堆中就是每個父節點的資料大於子節點中的資料。小根堆則相反，每個父節點的資料小於子節點。下面就是一個大根堆跟一個小根堆

                           大根堆                                                                                        小根堆

   堆排序的原理就是每次將未排序陣列構建成一個大根堆或者是一個小根堆，得到根節點便是未排序陣列中的最大或者是最小值，然後將根節點即陣列中第一個資料跟未排序陣列中的最後一個元素即進行交換。然後將未排序陣列的數量減一，再次構建大根堆或者小根堆。以此類推，直到未排序陣列剩下一個元素。下面以大根堆為例：

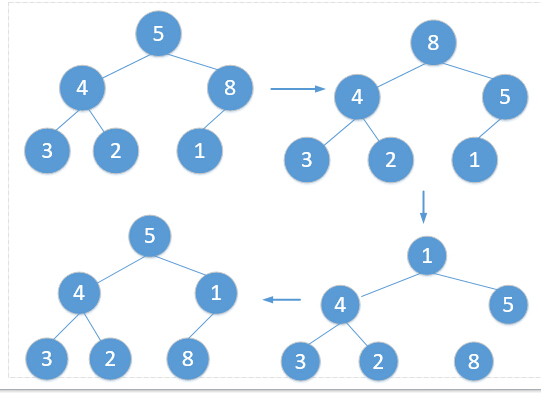
   按照上圖的做法不斷迴圈直到最後未排序陣列中剩下一個元素，排序完成。

   下面是堆排序陣列的java實現程式碼：HeapSort進行構建大根堆並且實現堆中最大元素與最後一個元素的交換，BuildHeap實現構建大根堆

 public static void HeapSort(int[] array , int lengthIndex){
            // 將未排序陣列構建大根堆
            BuildHeap(array,lengthIndex);
            // 交換堆中的根節點和最後一個節點
            int temp = array[lengthIndex];
            array[lengthIndex] = array[0];
            array[0] = temp;
            // 判斷未排序元素是否大於一個
            if(lengthIndex > 0){
                 HeapSort(array, lengthIndex - 1);
            }   
        }
        
        // 構建大根堆
        public static void BuildHeap(int[] array,int lengthIndex){
            int temp = 0;
            // 迴圈堆中的所有父節點和它兩個子節點進行比較，保證父節點是最大值
            for(int i = lengthIndex/2;i>=0;i--){
                if( (2*i+1) <= lengthIndex && array[i]<array[2*i+1] ){
                    temp = array[i];
                    array[i] = array[2*i+1];
                    array[2*i+1] = temp;
                }
                if((2*i+2) <= lengthIndex && array[i]<array[2*i+2] ){
                    temp = array[i];
                    array[i] = array[2*i+2];
                    array[2*i+2] = temp;
                }
            }
        }

堆排序的空間複雜度為O(1),時間複雜度為O(nlogn)。

原文地址：http://www.cnblogs.com/huangweikun/p/5155808.html