題目：

有一個包含正數和負數的二維陣列。一個子矩陣是指在該二維陣列裡，任意相鄰的下標是1×1或更大的子陣列。一個子矩陣的和是指該子矩陣中所有元素的和。
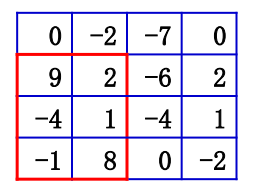
本題中，把具有最大和的子矩陣稱為最大子矩陣。例如，如下陣列的最大子矩陣位於左下角，其和為15。

輸入

是N×N個整數的陣列。第一行是一個正整數N，表示二維方陣的大小。接下來是N2個整數（由空格和換行隔開）。該陣列的N2個整數，是以行序給出的。先是第一行的數，由左到右；然後是第二的數，由左到右，等等。N可能達到100，陣列元素的範圍是[-127，127]。

輸出：

輸出是最大子矩陣的和。

思路：

1、此問題是“最大欄位和”問題的推廣。
2、程式碼具體過程如下：

程式碼：

#include<cstdio>
#include<cstring>

int n;
int a[110][110];
int b[110];

int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=0; i<n; i++)
            for(int j=0; j<n; j++)
                scanf("%d",&a[i][j]);

        int Max = -32767;
        for(int i=0; i<n; i++)
        {
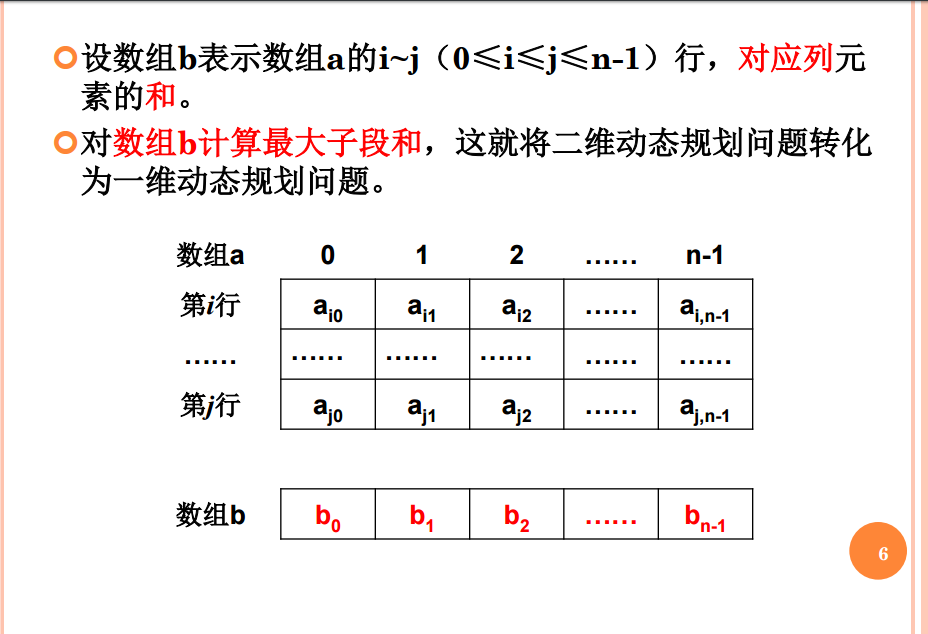
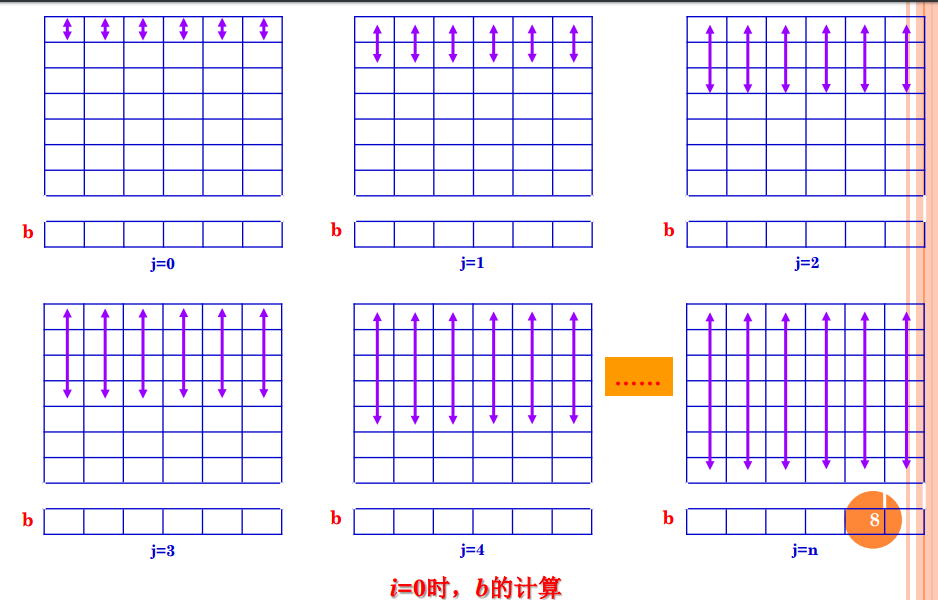
            //陣列b表示i~j行，對應列元素的和
            //將二維動態規劃問題轉化為一維動態規劃問題
            memset(b, 0, sizeof(b));
            for(int j=i; j<n; j++)
            {
                //下面是針對陣列b求最大子段和的動態規劃演算法
                int sum=0;
                for(int k=0; k<n; k++)
                {
                    b[k] += a[j][k];
                    sum += b[k];
                    if(sum<0) sum = b[k];
                    if(sum>Max) Max = sum;
                }
            }
        }
        printf("%d\n",Max);
    }

    return 0;
}