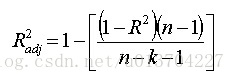迴歸預測評估指標

標註說明

f

評價指標

• MAE(Mean Absolute Error) 平均絕對誤差
  
  MAE=1n∑i=1n|fi−yi|
  MAE = \frac{1}{n}\sum_{i=1}^n|f_i-y_i|
• MSE(Mean Square Error) 平均平方差/均方誤差是迴歸任務最常用的效能度量。
  
  MSE=1n∑i=1n(fi−yi)2
  MSE=\frac{1}{n}\sum_{i=1}^n{(f_i-y_i)^2}

• RMSE(Root Mean Square Error) 方均根差
  

  RMSE=MSE‾‾‾‾‾√
  RMSE=\sqrt{MSE}
  
  缺點：因為它使用的是平均誤差，而平均誤差對異常點較敏感，如果迴歸器對某個點的迴歸值很不合理，那麼它的誤差則比較大，從而會對RMSE的值有較大影響，即平均值是非魯棒的。

• MAPE
  全稱是Mean Absolute Percentage Error（WikiPedia）, 也叫mean absolute percentage deviation (MAPD)，在統計領域是一個預測準確性的衡量指標。
  

  MAPE=100n∑t=1n|yi−fiyi|
  MAPE=\frac{100}{n}\sum_{t=1}^{n}|\frac{y_i-f_i}{y_i}|

• R平方
  y¯

  \bar{y}
  表示觀測資料的平均值
  殘差平方和
  
  SSres=∑(yi−fi)2
  SS_{res}=\sum{(y_i-f_i)^2}
  
  總平均值
  
  SStot=∑(yi−y¯)2
  SS_{tot}=\sum{(y_i-\bar{y})^2}
  
  R平方
  
  r2=1−SSresSStot=1−∑(yi−fi)2∑(yi−y¯)2
  r^2=1-\frac{SS_{res}}{SS_{tot}}=1-\frac{\sum{(y_i-f_i)^2}}{\sum{(y_i-\bar{y})^2}}
  
  R平方是多元迴歸中的迴歸平方和佔總平方和的比例,它是度量多元迴歸方程中擬合程度的一個統計量,反映了在因變數y
  y
  的變差中被估計的迴歸方程所解釋的比例。
  R平方越接近1,表明迴歸平方和佔總平方和的比例越大,迴歸線與各觀測點越接近,用x
  x
  的變化來解釋y
  y
  值變差的部分就越多,迴歸的擬合程度就越好。

• 校正R平方
  http://www.statisticshowto.com/adjusted-r2/
  

  where: N is the number of points in your data sample.
  K is the number of independent regressors, i.e. the number of variables in your model, excluding the constant

• RMSPE
  

  RMSPE=1n∑i=1n(yi−ŷ iyi)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾⎷
  \textrm{RMSPE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left(\frac{y_i - \hat{y}_i}{y_i}\right)^2}
  
  where yi
  y_i
  denotes the sales of a single store on a single day and ŷ i
  \hat{y}_i
  denotes the corresponding prediction.

https://www.kaggle.com/cast42/xgboost-in-python-with-rmspe-v2/code

• RMSLE(Root Mean Squared Logarithmic Error) Kaggle 上用的一個指標https://www.kaggle.com/wiki/RootMeanSquaredLogarithmicError

def rmsle(predicted,real):
    sum=0.0
    for x in range(len(predicted)):
        p = np.log(predicted[x]+1)
        r = np.log(real[x]+1)
        sum = sum + (p - r)**2
    return (sum/len(predicted))**0.5

# https://www.kaggle.com/jpopham91/rmlse-vectorized
# vectorized error calc
def rmsle(y, y0):
    assert len(y) == len(y0)
    return np.sqrt(np.mean(np.power(np.log1p(y)-np.log1p(y0), 2)))