NYOJ--重建二叉樹

輸入

輸入有多組資料（少於100組），以檔案結尾結束。
每組資料僅一行，包括兩個字串，中間用空格隔開，分別表示二叉樹的後序和中序序列（字串長度小於26，輸入資料保證合法）。

輸出

每組輸出資料單獨佔一行，輸出對應得先序序列。

樣例輸入

ACBFGED ABCDEFG
CDAB CBAD

樣例輸出

DBACEGF
BCAD

來源

原創

解析：這是一道資料結構中很水的題，可惜自己因為檔案結束符EOF這個TLE了很多次，唉……粗心哈！先簡單說一下二叉樹的遍歷

先序遍歷二叉樹：先序遍歷根節點，先序遍歷左子樹，先序遍歷右子樹，也就是NLR

中序遍歷二叉樹：中序遍歷左子樹，中序遍歷根節點，中序遍歷右子樹，也就是LNR

後序遍歷二叉樹：後序遍歷左子樹，後序遍歷右子樹，後序遍歷根節點，也就是LRN

要想由這三種遍歷二叉樹的序列重建唯一的二叉樹則至少得有兩種遍歷序列，且這兩種中一定要有中序序列，也就是先序+中序-->二叉樹  或者  後序+中序-->二叉樹，而先序+中序得不到唯一的二叉樹。

下面看一下這三種遍歷的特點，首先先序序列總是先遍歷根節點，所以它的序列的第一個必然是整個二叉樹的根節點，相反，後序遍歷的序列最後一個必然是二叉樹的根節點，通過缺點了二叉樹的根節點，在中序序列中找到這個根節點，因為中序序列是先遍歷左字數再遍歷根節點，然後是右子樹，所以在中序序列中的根節點左邊的節點全都是左子樹的，右邊的序列都應該是右子樹的，接著遞迴的應用就可以得到整個二叉樹了(不知道說清楚的沒)

後序序列：ACBFGED

中序序列：ABCDEFG

首先確定D是整個二叉樹的根節點，然後在中序序列中找到D則其左邊的ABC就是D的左子樹，EFG就是 D的右子樹。

提取出左字數的後序和中序序列

後序序列：ACB

中序序列: ABC

後序序列的最後一個字元是B則B是當前子樹的根節點，然後在中序序列中找到B則左邊的A是B的左子樹,C是B的右子樹。

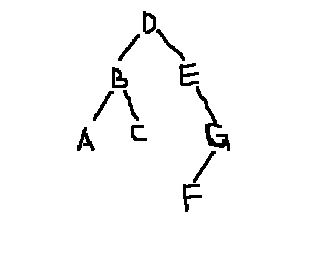
以此遞推就可以得到整個二叉樹的結構了，如下圖所示

同樣知道先序序列和中序序列後也可以構建出唯一的二叉樹，掌握的思想，下面就是用程式碼實現的事情了。

程式碼本著重建二叉樹的原則，並沒考慮太多OJ時間和空間的限制，但AC還是可以的，在程式碼中我右加上了先序+中序-->二叉樹的函式

當然在實際的OJ上做類似的題時不用那麼麻煩根根節點分配空間，直接輸出就好了，我只不過是想將二叉樹建立起來，看起來比較直觀而已

#include <stdio.h>
#include <malloc.h>
#include <string.h>
//二叉連結串列
typedef struct node{
	char data;//節點資料元素
	struct node *lchild;//指向左孩子
	struct node *rchild;//指向右孩子
}BiNode,*BTree;
//利用後序和中序建立二叉樹
void GetPreOrder(char *last,char *mid,BTree &T,int len)
{
	if(len==0)
	{
		T = NULL;
		return;
	}
	//取出後序序列中的最後一個節點
	char ch=last[len-1];
	int index=0;
	//在中序序列中進行查詢根節點，並用index記錄其在序列中的索引
	while(mid[index]!=ch)
	{
		index++;
	}
	//給根節點分配空間
	T=(BTree)malloc(sizeof(BiNode));
	T->data=mid[index];
	//建立左子樹
	GetPreOrder(last,mid,T->lchild,index);
	//建立右子樹
	GetPreOrder(last+index,mid+index+1,T->rchild,len-index-1);
}
void GetPostOrder(char *prim,char *mid,BTree &T,int len)
{
	if(len==0)
	{
		T=NULL;
		return;
	}
	//提出先序序列中的第一個節點
	char ch=prim[0];
	int index=0;
	//在中序序列中查詢當前根節點，並用index記錄其在序列中的位置
	while(mid[index]!=ch)
	{
		index++;
	}
	//給根節點分配空間
	T=(BTree)malloc(sizeof(BiNode));
	T->data=mid[index];
	//建立左子樹
	GetPostOrder(prim+1,mid,T->lchild,index);
	//建立右子樹
	GetPostOrder(prim+index+1,mid+index+1,T->rchild,len-index-1);
}
//先序輸出二叉樹
void PreOrder(BTree T)
{
	if(T!=NULL)
	{
		printf("%c",T->data);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}
//後序輸出二叉樹
void PostOrder(BTree T)
{
	if(T!=NULL)
	{
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		printf("%c",T->data);
	}
}
int main()
{
	char first[26],mid[26],last[26];
	while(scanf("%s%s",last,mid)!=EOF)
	{
		BTree T=NULL;
		GetPreOrder(last,mid,T,strlen(last));
		PreOrder(T);
// 		GetPostOrder(last,mid,T,strlen(last));
// 		PostOrder(T);
		printf("\n");
	}
	return 0;
}