JavaScript 函數語言程式設計介紹

探索函數語言程式設計，透過它讓你的程式更具有可讀性和易於除錯

當 Brendan Eich 在 1995 年創造 JavaScript 時，他原本打算將 Scheme 移植到瀏覽器裡 。Scheme 作為 Lisp 的方言，是一種函數語言程式設計語言。而當 Eich 被告知新的語言應該是一種可以與 Java 相比的指令碼語言後，他最終確立了一種擁有 C 風格語法的語言（也和 Java 一樣），但將函式視作一等公民。而 Java 直到版本 8 才從技術上將函式視為一等公民，雖然你可以用匿名類來模擬它。這個特性允許 JavaScript 透過函式式正規化程式設計。

JavaScript 是一個多正規化語言，允許你自由地混合和使用物件導向式、過程式和函式式的程式設計正規化。最近，函數語言程式設計越來越火熱。在諸如 Angular 和 React 這樣的框架中，透過使用不可變資料結構可以切實提高效能。不可變是函數語言程式設計的核心原則，它以及純函式使得編寫和除錯程式變得更加容易。使用函式來代替程式的迴圈可以提高程式的可讀性並使它更加優雅。總之，函數語言程式設計擁有很多優點。

什麼不是函數語言程式設計

在討論什麼是函數語言程式設計前，讓我們先排除那些不屬於函數語言程式設計的東西。實際上它們是你需要丟棄的語言元件（再見，老朋友）：

• 迴圈：
  • while
  • do...while
  • for
  • for...of
  • for...in
• 用 var 或者 let 來宣告變數
• 沒有返回值的函式
• 改變物件的屬性 (比如: o.x = 5;)
• 改變陣列本身的方法：
  • copyWithin
  • fill
  • pop
  • push
  • reverse
  • shift
  • sort
  • splice
  • unshift
• 改變對映本身的方法：
  • clear
  • delete
  • set
• 改變集合本身的方法：
  • add
  • clear
  • delete

脫離這些特性應該如何編寫程式呢？這是我們將在後面探索的問題。

純函式

你的程式中包含函式不一定意味著你正在進行函數語言程式設計。函式式正規化將純函式pure function和非純函式impure function區分開。鼓勵你編寫純函式。純函式必須滿足下面的兩個屬性：

• 引用透明：函式在傳入相同的引數後永遠返回相同的返回值。這意味著該函式不依賴於任何可變狀態。
• 無副作用：函式不能導致任何副作用。副作用可能包括 I/O（比如向終端或者日誌檔案寫入），改變一個不可變的物件，對變數重新賦值等等。

我們來看一些例子。首先，multiply 就是一個純函式的例子，它在傳入相同的引數後永遠返回相同的返回值，並且不會導致副作用。

function multiply(a, b) {
  return a * b;
}

下面是非純函式的例子。canRide 函式依賴捕獲的 heightRequirement 變數。被捕獲的變數不一定導致一個函式是非純函式，除非它是一個可變的變數（或者可以被重新賦值）。這種情況下使用 let 來宣告這個變數，意味著可以對它重新賦值。multiply 函式是非純函式，因為它會導致在 console 上輸出。

let heightRequirement = 46;

// Impure because it relies on a mutable (reassignable) variable.
function canRide(height) {
  return height >= heightRequirement;
}

// Impure because it causes a side-effect by logging to the console.
function multiply(a, b) {
  console.log('Arguments: ', a, b);
  return a * b;
}

下面的列表包含著 JavaScript 內建的非純函式。你可以指出它們不滿足兩個屬性中的哪個嗎？

• console.log
• element.addEventListener
• Math.random
• Date.now
• $.ajax (這裡 $ 代表你使用的 Ajax 庫)

理想的程式中所有的函式都是純函式，但是從上面的函式列表可以看出，任何有意義的程式都將包含非純函式。大多時候我們需要進行 AJAX 呼叫，檢查當前日期或者獲取一個隨機數。一個好的經驗法則是遵循 80/20 規則：函式中有 80％ 應該是純函式，剩下的 20％ 的必要性將不可避免地是非純函式。

使用純函式有幾個優點：

• 它們很容易匯出和除錯，因為它們不依賴於可變的狀態。
• 返回值可以被快取或者“記憶”來避免以後重複計算。
• 它們很容易測試，因為沒有需要模擬（mock）的依賴（比如日誌，AJAX，資料庫等等）。

你編寫或者使用的函式返回空（換句話說它沒有返回值），那代表它是非純函式。

不變性

讓我們回到捕獲變數的概念上。來看看 canRide 函式。我們認為它是一個非純函式，因為 heightRequirement 變數可以被重新賦值。下面是一個構造出來的例子來說明如何用不可預測的值來對它重新賦值。

let heightRequirement = 46;

function canRide(height) {
  return height >= heightRequirement;
}

// Every half second, set heightRequirement to a random number between 0 and 200.
setInterval(() => heightRequirement = Math.floor(Math.random() * 201), 500);

const mySonsHeight = 47;

// Every half second, check if my son can ride.
// Sometimes it will be true and sometimes it will be false.
setInterval(() => console.log(canRide(mySonsHeight)), 500);

我要再次強調被捕獲的變數不一定會使函式成為非純函式。我們可以透過只是簡單地改變 heightRequirement 的宣告方式來使 canRide 函式成為純函式。

const heightRequirement = 46;

function canRide(height) {
  return height >= heightRequirement;
}

透過用 const 來宣告變數意味著它不能被再次賦值。如果嘗試對它重新賦值，執行時引擎將丟擲錯誤；那麼，如果用物件來代替數字來儲存所有的“常量”怎麼樣？

const constants = {
  heightRequirement: 46,
  // ... other constants go here
};

function canRide(height) {
  return height >= constants.heightRequirement;
}

我們用了 const ，所以這個變數不能被重新賦值，但是還有一個問題：這個物件可以被改變。下面的程式碼展示了，為了真正使其不可變，你不僅需要防止它被重新賦值，你也需要不可變的資料結構。JavaScript 語言提供了 Object.freeze 方法來阻止物件被改變。

'use strict';

// CASE 1: 物件的屬性是可變的，並且變數可以被再次賦值。
let o1 = { foo: 'bar' };

// 改變物件的屬性
o1.foo = 'something different';

// 對變數再次賦值
o1 = { message: "I'm a completely new object" };


// CASE 2: 物件的屬性還是可變的，但是變數不能被再次賦值。
const o2 = { foo: 'baz' };

// 仍然能改變物件
o2.foo = 'Something different, yet again';

// 不能對變數再次賦值
// o2 = { message: 'I will cause an error if you uncomment me' }; // Error!


// CASE 3: 物件的屬性是不可變的，但是變數可以被再次賦值。
let o3 = Object.freeze({ foo: "Can't mutate me" });

// 不能改變物件的屬性
// o3.foo = 'Come on, uncomment me. I dare ya!'; // Error!

// 還是可以對變數再次賦值
o3 = { message: "I'm some other object, and I'm even mutable -- so take that!" };


// CASE 4: 物件的屬性是不可變的，並且變數不能被再次賦值。這是我們想要的！！！！！！！！
const o4 = Object.freeze({ foo: 'never going to change me' });

// 不能改變物件的屬性
// o4.foo = 'talk to the hand' // Error!

// 不能對變數再次賦值
// o4 = { message: "ain't gonna happen, sorry" }; // Error

不變性適用於所有的資料結構，包括陣列、對映和集合。它意味著不能呼叫例如 Array.prototype.push 等會導致本身改變的方法，因為它會改變已經存在的陣列。可以透過建立一個含有原來元素和新加元素的新陣列，而不是將新元素加入一個已經存在的陣列。其實所有會導致陣列本身被修改的方法都可以透過一個返回修改好的新陣列的函式代替。

'use strict';

const a = Object.freeze([4, 5, 6]);

// Instead of: a.push(7, 8, 9);
const b = a.concat(7, 8, 9);

// Instead of: a.pop();
const c = a.slice(0, -1);

// Instead of: a.unshift(1, 2, 3);
const d = [1, 2, 3].concat(a);

// Instead of: a.shift();
const e = a.slice(1);

// Instead of: a.sort(myCompareFunction);
const f = R.sort(myCompareFunction, a); // R = Ramda

// Instead of: a.reverse();
const g = R.reverse(a); // R = Ramda

// 留給讀者的練習:
// copyWithin
// fill
// splice

對映 和 集合 也很相似。可以透過返回一個新的修改好的對映或者集合來代替使用會修改其本身的函式。

const map = new Map([
  [1, 'one'],
  [2, 'two'],
  [3, 'three']
]);

// Instead of: map.set(4, 'four');
const map2 = new Map([...map, [4, 'four']]);

// Instead of: map.delete(1);
const map3 = new Map([...map].filter(([key]) => key !== 1));

// Instead of: map.clear();
const map4 = new Map();

const set = new Set(['A', 'B', 'C']);

// Instead of: set.add('D');
const set2 = new Set([...set, 'D']);

// Instead of: set.delete('B');
const set3 = new Set([...set].filter(key => key !== 'B'));

// Instead of: set.clear();
const set4 = new Set();

我想提一句如果你在使用 TypeScript（我非常喜歡 TypeScript），你可以用 Readonly<T>、ReadonlyArray<T>、ReadonlyMap<K, V> 和 ReadonlySet<T> 介面來在編譯期檢查你是否嘗試更改這些物件，有則丟擲編譯錯誤。如果在對一個物件字面量或者陣列呼叫 Object.freeze，編譯器會自動推斷它是隻讀的。由於對映和集合在其內部表達，所以在這些資料結構上呼叫 Object.freeze 不起作用。但是你可以輕鬆地告訴編譯器它們是隻讀的變數。

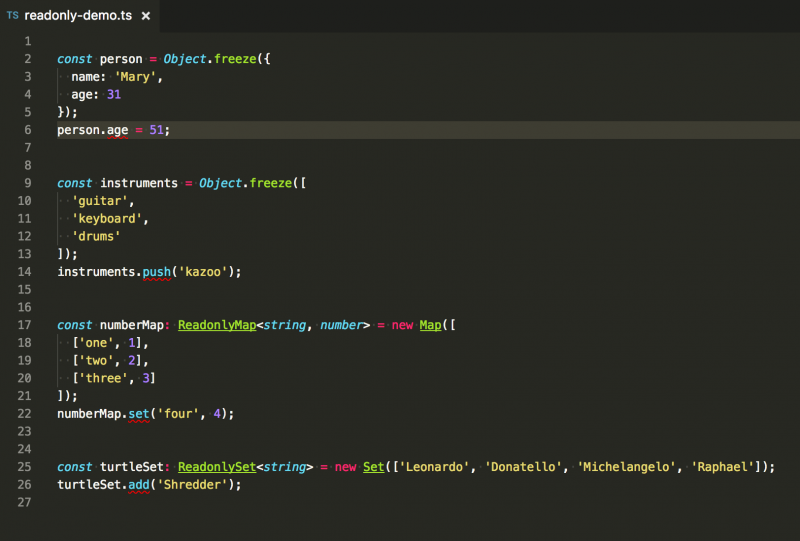
TypeScript 只讀介面

好，所以我們可以透過建立新的物件來代替修改原來的物件，但是這樣不會導致效能損失嗎？當然會。確保在你自己的應用中做了效能測試。如果你需要提高效能，可以考慮使用 Immutable.js。Immutable.js 用持久的資料結構 實現了連結串列、堆疊、對映、集合和其他資料結構。使用瞭如同 Clojure 和 Scala 這樣的函式式語言中相同的技術。

// Use in place of `[]`.
const list1 = Immutable.List(['A', 'B', 'C']);
const list2 = list1.push('D', 'E');

console.log([...list1]); // ['A', 'B', 'C']
console.log([...list2]); // ['A', 'B', 'C', 'D', 'E']


// Use in place of `new Map()`
const map1 = Immutable.Map([
  ['one', 1],
  ['two', 2],
  ['three', 3]
]);
const map2 = map1.set('four', 4);

console.log([...map1]); // [['one', 1], ['two', 2], ['three', 3]]
console.log([...map2]); // [['one', 1], ['two', 2], ['three', 3], ['four', 4]]


// Use in place of `new Set()`
const set1 = Immutable.Set([1, 2, 3, 3, 3, 3, 3, 4]);
const set2 = set1.add(5);

console.log([...set1]); // [1, 2, 3, 4]
console.log([...set2]); // [1, 2, 3, 4, 5]

函式組合

記不記得在中學時我們學過一些像 (f ∘ g)(x) 的東西？你那時可能想，“我什麼時候會用到這些？”，好了，現在就用到了。你準備好了嗎？f ∘ g讀作 “函式 f 和函式 g 組合”。對它的理解有兩種等價的方式，如等式所示： (f ∘ g)(x) = f(g(x))。你可以認為 f ∘ g 是一個單獨的函式，或者視作將呼叫函式 g 的結果作為引數傳給函式 f。注意這些函式是從右向左依次呼叫的，先執行 g，接下來執行 f。

關於函式組合的幾個要點:

1. 我們可以組合任意數量的函式（不僅限於 2 個）。
2. 組合函式的一個方式是簡單地把一個函式的輸出作為下一個函式的輸入（比如 f(g(x))）。

// h(x) = x + 1
// number -> number
function h(x) {
  return x + 1;
}

// g(x) = x^2
// number -> number
function g(x) {
  return x * x;
}

// f(x) = convert x to string
// number -> string
function f(x) {
  return x.toString();
}

// y = (f ∘ g ∘ h)(1)
const y = f(g(h(1)));
console.log(y); // '4'

Ramda 和 lodash 之類的庫提供了更優雅的方式來組合函式。我們可以在更多的在數學意義上處理函式組合，而不是簡單地將一個函式的返回值傳遞給下一個函式。我們可以建立一個由這些函式組成的單一複合函式(就是 (f ∘ g)(x))。

// h(x) = x + 1
// number -> number
function h(x) {
  return x + 1;
}

// g(x) = x^2
// number -> number
function g(x) {
  return x * x;
}

// f(x) = convert x to string
// number -> string
function f(x) {
  return x.toString();
}

// R = Ramda
// composite = (f ∘ g ∘ h)
const composite = R.compose(f, g, h);

// Execute single function to get the result.
const y = composite(1);
console.log(y); // '4'

好了，我們可以在 JavaScript 中組合函式了。接下來呢？好，如果你已經入門了函數語言程式設計，理想中你的程式將只有函式的組合。程式碼裡沒有迴圈（for, for...of, for...in, while, do），基本沒有。你可能覺得那是不可能的。並不是這樣。我們下面的兩個話題是：遞迴和高階函式。

遞迴

假設你想實現一個計算數字的階乘的函式。 讓我們回顧一下數學中階乘的定義：

n! = n * (n-1) * (n-2) * ... * 1.

n! 是從 n 到 1 的所有整數的乘積。我們可以編寫一個迴圈輕鬆地計算出結果。

function iterativeFactorial(n) {
  let product = 1;
  for (let i = 1; i <= n; i++) {
    product *= i;
  }
  return product;
}

注意 product 和 i 都在迴圈中被反覆重新賦值。這是解決這個問題的標準過程式方法。如何用函式式的方法解決這個問題呢？我們需要消除迴圈，確保沒有變數被重新賦值。遞迴是函式式程式設計師的最有力的工具之一。遞迴需要我們將整體問題分解為類似整體問題的子問題。

計算階乘是一個很好的例子，為了計算 n! 我們需要將 n 乘以所有比它小的正整數。它的意思就相當於：

n! = n * (n-1)!

啊哈！我們發現了一個解決 (n-1)! 的子問題，它類似於整個問題 n!。還有一個需要注意的地方就是基礎條件。基礎條件告訴我們何時停止遞迴。 如果我們沒有基礎條件，那麼遞迴將永遠持續。 實際上，如果有太多的遞迴呼叫，程式會丟擲一個堆疊溢位錯誤。啊哈！

function recursiveFactorial(n) {
  // Base case -- stop the recursion
  if (n === 0) {
    return 1; // 0! is defined to be 1.
  }
  return n * recursiveFactorial(n - 1);
}

然後我們來計算 recursiveFactorial(20000) 因為……，為什麼不呢？當我們這樣做的時候，我們得到了這個結果：

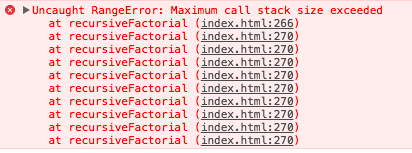
堆疊溢位錯誤

這裡發生了什麼？我們得到一個堆疊溢位錯誤！這不是無窮的遞迴導致的。我們已經處理了基礎條件(n === 0 的情況)。那是因為瀏覽器的堆疊大小是有限的，而我們的程式碼使用了越過了這個大小的堆疊。每次對 recursiveFactorial 的呼叫導致了新的幀被壓入堆疊中，就像一個盒子壓在另一個盒子上。每當 recursiveFactorial 被呼叫，一個新的盒子被放在最上面。下圖展示了在計算 recursiveFactorial(3) 時堆疊的樣子。注意在真實的堆疊中，堆疊頂部的幀將儲存在執行完成後應該返回的記憶體地址，但是我選擇用變數 r 來表示返回值，因為 JavaScript 開發者一般不需要考慮記憶體地址。

遞迴計算 3! 的堆疊（三次乘法）

你可能會想象當計算 n = 20000 時堆疊會更高。我們可以做些什麼最佳化它嗎？當然可以。作為 ES2015 (又名 ES6) 標準的一部分，有一個最佳化用來解決這個問題。它被稱作尾呼叫最佳化proper tail calls optimization（PTC）。當遞迴函式做的最後一件事是呼叫自己並返回結果的時候，它使得瀏覽器刪除或者忽略堆疊幀。實際上，這個最佳化對於相互遞迴函式也是有效的，但是為了簡單起見，我們還是來看單一遞迴函式。

你可能會注意到，在遞迴函式呼叫之後，還要進行一次額外的計算（n * r）。那意味著瀏覽器不能透過 PTC 來最佳化遞迴；然而，我們可以透過重寫函式使最後一步變成遞迴呼叫以便最佳化。一個竅門是將中間結果（在這裡是 product）作為引數傳遞給函式。

'use strict';

// Optimized for tail call optimization.
function factorial(n, product = 1) {
  if (n === 0) {
    return product;
  }
  return factorial(n - 1, product * n)
}

讓我們來看看最佳化後的計算 factorial(3) 時的堆疊。如下圖所示，堆疊不會增長到超過兩層。原因是我們把必要的資訊都傳到了遞迴函式中（比如 product）。所以，在 product 被更新後，瀏覽器可以丟棄掉堆疊中原先的幀。你可以在圖中看到每次最上面的幀下沉變成了底部的幀，原先底部的幀被丟棄，因為不再需要它了。

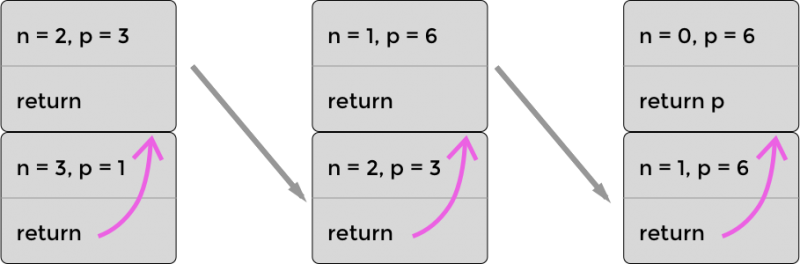
遞迴計算 3! 的堆疊（三次乘法）使用 PTC

現在選一個瀏覽器執行吧，假設你在使用 Safari，你會得到 Infinity（它是比在 JavaScript 中能表達的最大值更大的數）。但是我們沒有得到堆疊溢位錯誤，那很不錯！現在在其他的瀏覽器中呢怎麼樣呢？Safari 可能現在乃至將來是實現 PTC 的唯一一個瀏覽器。看看下面的相容性表格：

PTC 相容性

其他瀏覽器提出了一種被稱作語法級尾呼叫syntactic tail calls（STC）的競爭標準。“語法級”意味著你需要用新的語法來標識你想要執行尾遞迴最佳化的函式。即使瀏覽器還沒有廣泛支援，但是把你的遞迴函式寫成支援尾遞迴最佳化的樣子還是一個好主意。

高階函式

我們已經知道 JavaScript 將函式視作一等公民，可以把函式像其他值一樣傳遞。所以，把一個函式傳給另一個函式也很常見。我們也可以讓函式返回一個函式。就是它！我們有高階函式。你可能已經很熟悉幾個在 Array.prototype 中的高階函式。比如 filter、map 和 reduce 就在其中。對高階函式的一種理解是：它是接受（一般會呼叫）一個回撥函式引數的函式。讓我們來看看一些內建的高階函式的例子：

const vehicles = [
  { make: 'Honda', model: 'CR-V', type: 'suv', price: 24045 },
  { make: 'Honda', model: 'Accord', type: 'sedan', price: 22455 },
  { make: 'Mazda', model: 'Mazda 6', type: 'sedan', price: 24195 },
  { make: 'Mazda', model: 'CX-9', type: 'suv', price: 31520 },
  { make: 'Toyota', model: '4Runner', type: 'suv', price: 34210 },
  { make: 'Toyota', model: 'Sequoia', type: 'suv', price: 45560 },
  { make: 'Toyota', model: 'Tacoma', type: 'truck', price: 24320 },
  { make: 'Ford', model: 'F-150', type: 'truck', price: 27110 },
  { make: 'Ford', model: 'Fusion', type: 'sedan', price: 22120 },
  { make: 'Ford', model: 'Explorer', type: 'suv', price: 31660 }
];

const averageSUVPrice = vehicles
  .filter(v => v.type === 'suv')
  .map(v => v.price)
  .reduce((sum, price, i, array) => sum + price / array.length, 0);

console.log(averageSUVPrice); // 33399

注意我們在一個陣列物件上呼叫其方法，這是物件導向程式設計的特性。如果我們想要更函式式一些，我們可以用 Rmmda 或者 lodash/fp 提供的函式。注意如果我們使用 R.compose 的話，需要倒轉函式的順序，因為它從右向左依次呼叫函式（從底向上）；然而，如果我們想從左向右呼叫函式就像上面的例子，我們可以用 R.pipe。下面兩個例子用了 Rmmda。注意 Rmmda 有一個 mean 函式用來代替 reduce 。

const vehicles = [
  { make: 'Honda', model: 'CR-V', type: 'suv', price: 24045 },
  { make: 'Honda', model: 'Accord', type: 'sedan', price: 22455 },
  { make: 'Mazda', model: 'Mazda 6', type: 'sedan', price: 24195 },
  { make: 'Mazda', model: 'CX-9', type: 'suv', price: 31520 },
  { make: 'Toyota', model: '4Runner', type: 'suv', price: 34210 },
  { make: 'Toyota', model: 'Sequoia', type: 'suv', price: 45560 },
  { make: 'Toyota', model: 'Tacoma', type: 'truck', price: 24320 },
  { make: 'Ford', model: 'F-150', type: 'truck', price: 27110 },
  { make: 'Ford', model: 'Fusion', type: 'sedan', price: 22120 },
  { make: 'Ford', model: 'Explorer', type: 'suv', price: 31660 }
];

// Using `pipe` executes the functions from top-to-bottom. 
const averageSUVPrice1 = R.pipe(
  R.filter(v => v.type === 'suv'),
  R.map(v => v.price),
  R.mean
)(vehicles);

console.log(averageSUVPrice1); // 33399

// Using `compose` executes the functions from bottom-to-top.
const averageSUVPrice2 = R.compose(
  R.mean,
  R.map(v => v.price),
  R.filter(v => v.type === 'suv')
)(vehicles);

console.log(averageSUVPrice2); // 33399

使用函式式方法的優點是清楚地分開了資料（vehicles）和邏輯（函式 filter，map 和 reduce）。物件導向的程式碼相比之下把資料和函式用以方法的物件的形式混合在了一起。

柯里化

不規範地說，柯里化currying是把一個接受 n 個引數的函式變成 n 個每個接受單個引數的函式的過程。函式的 arity 是它接受引數的個數。接受一個引數的函式是 unary，兩個的是 binary，三個的是 ternary，n 個的是 n-ary。那麼，我們可以把柯里化定義成將一個 n-ary 函式轉換成 n 個 unary 函式的過程。讓我們透過簡單的例子開始，一個計算兩個向量點積的函式。回憶一下線性代數，兩個向量 [a, b, c] 和 [x, y, z] 的點積是 ax + by + cz。

function dot(vector1, vector2) {
  return vector1.reduce((sum, element, index) => sum += element * vector2[index], 0);
}

const v1 = [1, 3, -5];
const v2 = [4, -2, -1];

console.log(dot(v1, v2)); // 1(4) + 3(-2) + (-5)(-1) = 4 - 6 + 5 = 3

dot 函式是 binary，因為它接受兩個引數；然而我們可以將它手動轉換成兩個 unary 函式，就像下面的例子。注意 curriedDot 是一個 unary 函式，它接受一個向量並返回另一個接受第二個向量的 unary 函式。

function curriedDot(vector1) {
  return function(vector2) {
    return vector1.reduce((sum, element, index) => sum += element * vector2[index], 0);
  }
}

// Taking the dot product of any vector with [1, 1, 1]
// is equivalent to summing up the elements of the other vector.
const sumElements = curriedDot([1, 1, 1]);

console.log(sumElements([1, 3, -5])); // -1
console.log(sumElements([4, -2, -1])); // 1

很幸運，我們不需要把每一個函式都手動轉換成柯里化以後的形式。Ramda 和 lodash 等庫可以為我們做這些工作。實際上，它們是柯里化的混合形式。你既可以每次傳遞一個引數，也可以像原來一樣一次傳遞所有引數。

function dot(vector1, vector2) {
  return vector1.reduce((sum, element, index) => sum += element * vector2[index], 0);
}

const v1 = [1, 3, -5];
const v2 = [4, -2, -1];

// Use Ramda to do the currying for us!
const curriedDot = R.curry(dot);

const sumElements = curriedDot([1, 1, 1]);

console.log(sumElements(v1)); // -1
console.log(sumElements(v2)); // 1

// This works! You can still call the curried function with two arguments.
console.log(curriedDot(v1, v2)); // 3

Ramda 和 lodash 都允許你“跳過”一些變數之後再指定它們。它們使用置位符來做這些工作。因為點積的計算可以交換兩項。傳入向量的順序不影響結果。讓我們換一個例子來闡述如何使用一個置位符。Ramda 使用雙下劃線作為其置位符。

const giveMe3 = R.curry(function(item1, item2, item3) {
  return `
    1: ${item1}
    2: ${item2}
    3: ${item3}
  `;
});

const giveMe2 = giveMe3(R.__, R.__, 'French Hens');   // Specify the third argument.
const giveMe1 = giveMe2('Partridge in a Pear Tree');  // This will go in the first slot.
const result = giveMe1('Turtle Doves');               // Finally fill in the second argument.

console.log(result);
// 1: Partridge in a Pear Tree
// 2: Turtle Doves
// 3: French Hens

在我們結束探討柯里化之前最後的議題是偏函式應用partial application。偏函式應用和柯里化經常同時出場，儘管它們實際上是不同的概念。一個柯里化的函式還是柯里化的函式，即使沒有給它任何引數。偏函式應用，另一方面是僅僅給一個函式傳遞部分引數而不是所有引數。柯里化是偏函式應用常用的方法之一，但是不是唯一的。

JavaScript 擁有一個內建機制可以不依靠柯里化來做偏函式應用。那就是 function.prototype.bind 方法。這個方法的一個特殊之處在於，它要求你將 this 作為第一個引數傳入。 如果你不進行物件導向程式設計，那麼你可以透過傳入 null 來忽略 this。

1function giveMe3(item1, item2, item3) {
  return `
    1: ${item1}
    2: ${item2}
    3: ${item3}
  `;
}

const giveMe2 = giveMe3.bind(null, 'rock');
const giveMe1 = giveMe2.bind(null, 'paper');
const result = giveMe1('scissors');

console.log(result);
// 1: rock
// 2: paper
// 3: scissors

總結

我希望你享受探索 JavaScript 中函數語言程式設計的過程。對一些人來說，它可能是一個全新的程式設計正規化，但我希望你能嘗試它。你會發現你的程式更易於閱讀和除錯。不變性還將允許你最佳化 Angular 和 React 的效能。

這篇文章基於 Matt 在 OpenWest 的演講 JavaScript the Good-er Parts. OpenWest 將在 6/12-15 ,2017 在 Salt Lake City, Utah 舉行。

---

作者簡介：

Matt Banz - Matt 於 2008 年五月在猶他大學獲得了數學學位畢業。一個月後他得到了一份 web 開發者的工作，他從那時起就愛上了它！在 2013 年，他在北卡羅萊納州立大學獲得了電腦科學碩士學位。他在 LDS 商學院和戴維斯學區社群教育計劃教授 Web 課程。他現在是就職於 Motorola Solutions 公司的高階前端開發者。

---

via: https://opensource.com/article/17/6/functional-javascript

作者：Matt Banz 譯者：trnhoe 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出