秀爾演算法：破解RSA加密的“不滅神話”

RSA加密曾被視為最可靠的加密演算法，直到秀爾演算法出現，打破了RSA的不滅神話。

RSA加密 VS 秀爾演算法

作為RSA加密技術的終結者——“太多運算，無法讀取”的秀爾演算法（Shor’s algorithm）不是透過暴力破解的方式找到最終密碼的，而是利用量子計算的並行性，可以快速分解出公約數，從而打破了RSA演算法的基礎（即假設我們不能很有效的分解一個已知的整數）。同時，秀爾演算法展示了因數分解這問題在量子計算機上可以很有效率的解決，所以一個足夠大的量子計算機可以破解RSA。

RSA加密“曾經”之所以強大，是因為它對極大整數做因數分解的難度決定了RSA演算法的可靠性。將兩個質數相乘是件很容易的事情，但要找到一個龐大數字的質因子卻非常困難。這便是大量現代科技的依靠之處，RSA加密就是憑藉其簡潔性迅速風靡。

然而，有一種技術可以讓RSA加密無用武之地。秀爾演算法可以破解RSA，但是怎樣才能讓它真正見效呢？

我們這裡並非建議你同時嘗試所有可能的質因子。

而是使用（相對）簡潔的語句：

如果我們快速找到下面這個週期函式的週期，

 f(x) = m^x (mod N)

我們便可以破解RSA加密。

秀爾五步走

那麼，秀爾演算法究竟是怎樣工作的呢？在秀爾五步法中，只有一步需要是需要用到量子計算機的，其他的步驟則都可以採用傳統方法解決。

第一步：

使用傳統最大公約數分解（gcd）演算法，也就是輾轉相除法。N是你需要嘗試的因子，m則是一個小於N的隨機正整數。

如果gcd（m，N）=1，則繼續。一旦你使用gcd找到一個因子，你便能獲得一個非凡因子，然後結束。

第二步：

找到週期 P

m mod N, m^2 mod N, m^3 mod N

這是使用量子計算的一步。

第三步：

如果週期P是奇數，回到第一步，選擇另一個隨機整數。如果不是，繼續下一步。

第四步：

檢驗

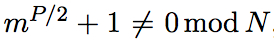
如果成立，則繼續第五步；反之，回到第一步。

第五步：

解

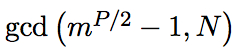
解得一個非凡素因數N的值，然後你便能破解RSA加密了。

第二步是怎樣實現的？

然而，量子計算機是如何找到函式週期的？這又為什麼如此重要？

我們來看一下週期 P ：

m mod N, m^2 mod N, m^3 mod N

(由於這是一個指數函式，我們可以將一個複雜的質數轉換成雙曲正弦、餘弦然後得到週期)

這個發現週期的過程需要依賴量子計算機同時計算許多狀態的能力，也就是狀態的“疊加”，因此我們能找到方程的週期。

我們需要這麼做：

1. 應用Hadamard gate來建立一個量子疊加態
2. 量子轉換使方程生效
3. 執行量子傅立葉變換

與傳統情況類似，在這些轉化之後，一個測量值將會產生一個近似方程週期的值（你可以獲得“波峰”，就像傅立葉變換中的，而準確性會更高一點）。使用量子傅立葉變換，我們能夠解決排序和因數問題，這二者相同。量子傅立葉變換可以讓一臺量子計算機進行相位估計（酉運算元特徵值的近似值）。

當你完成量子部分（第二步）的時候，你可以檢查一下週期的有效性，然後使用另一個傳統的最大公約數演算法得到金鑰的質因素。

有趣的是，由於這項技術並不是在於找到所有潛在質因數，而是找到潛在週期，你就不必嘗試很多隨機數直到找到一個成功的質因數N。如果P是奇數，那你不得不回到第一步，這裡

K是一個不同於N的質因素。因此，即使你加倍金鑰長度（N），尋找質因數也不會出現放緩的情況。RSA是不安全的，同樣加倍金鑰長度也不能幫你抵禦量子計算的洶湧來襲，而保障安全。

“破解RSA-2048（2048-bit）的金鑰可能需要耗費傳統電腦10億年的時間，而量子計算機只需要100秒就可以完成。”

——Dr. Krysta Svore, 微軟研究院

量子傅立葉變換被用於建立量子線路，使得秀爾演算法的物理實現成了量子計算機最為輕鬆的任務之一。

量子傅立葉變換：青出於藍

秀爾演算法的核心是發現順序，這樣便可以減少阿貝爾的隱子群問題，使用量子傅立葉變換便可以解決。——NIST 量子世界

量子傅立葉變換是許多量子演算法的關鍵所在。它並不加速尋找傳統傅立葉轉變，但是能夠在一個量子振幅內執行一個傅立葉變換。在一臺量子計算機上可以指數增長般快速處理量子傅立葉變換。雖然超過了直接對映經典傅立葉變換的範疇，量子計算機也可以做其他的事。例如，解決隱子群問題(也就是解決離散對數問題)，或是計數問題(解決了這個問題就可以解決現代密碼學中很多其他形式的密碼)。更重要的是，量子傅立葉變換可以應用到機器學習、化學、材料科學或者模擬量子系統。

秀爾演算法中只有一個步驟是需要在量子計算機上完成的，其他的都可以在普通的超級計算機上完成。量子計算機執行完子程式後就會將結果返回給超級計算機讓它繼續完成計算過程。量子計算機可能永遠不會是單獨存在的，而是一直和超級計算機配合執行任務，經過這樣的配合它們就可以破解RSA金鑰。

因為篇幅有限，很多數學細節和證明過程就不再贅述了，如果你對這些數學解釋感興趣，如果你具備線性代數、群論、高等數學的知識，你可以看看這些：

• Quantum Computer Science
• Quantum Information and Quantum Computation
• NIST Quantum Zoo  — 一個所有量子演算法的列表

*參考來源：medium，vulture對本文有貢獻，