YT15-HDU-Harry's parents had left him a lot of gold coins

不被看好的青春叫成長發表於2015-03-07
Go

Problem Description

 

Famous Harry Potter,who seemd to be a normal and poor boy,is actually a wizard.Everything changed when he had his birthday of ten years old.A huge man called 'Hagrid' found Harry and lead him to a new world full of magic power. 
If you've read this story,you probably know that Harry's parents had left him a lot of gold coins.Hagrid lead Harry to Gringotts(the bank hold up by Goblins). And they stepped into the room which stored the fortune from his father.Harry was astonishing ,coz there were piles of gold coins. 
The way of packing these coins by Goblins was really special.Only one coin was on the top,and three coins consisted an triangle were on the next lower layer.The third layer has six coins which were also consisted an triangle,and so on.On the ith layer there was an triangle have i coins each edge(totally i*(i+1)/2).The whole heap seemed just like a pyramid.Goblin still knew the total num of the layers,so it's up you to help Harry to figure out the sum of all the coins.

 

Input

 

The input will consist of some cases,each case takes a line with only one integer N(0<N<2^31).It ends with a single 0.

 

Output

 

對於每個輸入的N,輸出一行,採用科學記數法來計算金幣的總數(保留三位有效數字)

 

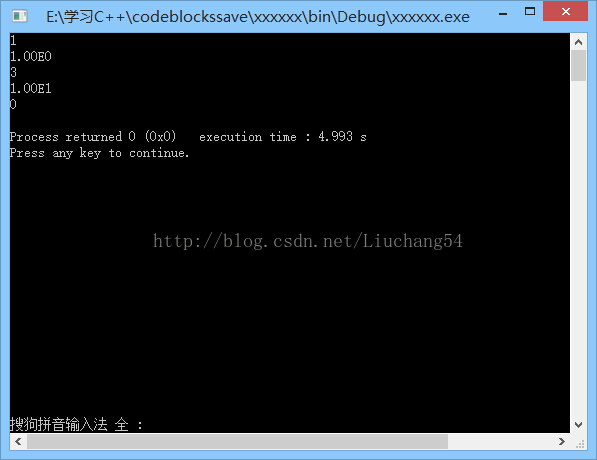
Sample Input

 

1
3
0

 

Sample Output

 

1.00E0
1.00E1

 

Hint

 

Hint
when N=1 ,There is 1 gold coins. 
when N=3 ,There is 1+3+6=10 gold coins.


程式碼如下：

#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{
    int n,i;
    double sum,m;
    while (cin>>n&&n!=0)
    {
        sum=(1.0*n*n*n+3.0*n*n+2.0*n)/6.0;      //注意資料型別
        m=(int) log10(sum);
        for (i=1;i<=m;i++)
            sum*=0.1;
        cout<<setiosflags(ios::fixed)<<setprecision(2)<<sum<<"E";         //控制輸出格式
        cout<<setiosflags(ios::fixed)<<setprecision(0)<<m<<endl;
    }
    return 0;
}


執行結果：

規律：

sum=1+3+6+10+15+……+n*(n+1)/2
   =(1^2-0)+(2^2-1)+(3^2-3)+(4^2-6)+(5^2-10)+……+(n^2-(n-1)*n/2)
   =1^2+2^2+3^2+4^2+5^2+……+n^2-(1+3+6+10+15+……+n*(n-1)/2)
   =n*(n+1)*(2*n+1)/6-sum+n*(n+1)/2
   =(1*n*n*n+3*n*n+2*n)/6

相關文章