百度ABC
ABC = AI+Big data + Cloud Computing
百度 基礎雲, 天像(智慧多媒體平臺),天算(智慧大資料平臺),天工(智慧物聯網平臺),天智(人工智慧平臺)
監督學習和無監督學習
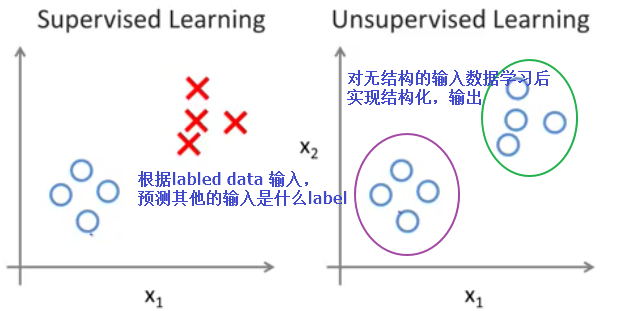
監督學習,就是人們常說的分類,通過已有的訓練樣本(即已知資料以及其對應的正確輸出)去訓練得到一個最優模型(這個模型屬於某個函式的集合,最優則表示在某個評價準則下是最佳的),再利用這個模型將所有的輸入對映為相應的輸出,對輸出進行簡單的判斷從而實現分類的目的,也就具有了對未知資料進行分類的能力。監督學習裡典型的例子就是KNN、SVM
無監督學習(也有人叫非監督學習,反正都差不多)則是另一種研究的比較多的學習方法,它與監督學習的不同之處,在於我們事先沒有任何正確的訓練樣本,而需要直接對一堆資料進行建模,找到其中可能的特徵。無監督學習裡典型的例子就是聚類了。聚類的目的在於把相似的東西聚在一起,而我們並不關心這一類是什麼。因此,一個聚類演算法通常只需要知道如何計算相似度就可以開始工作了。比如,人類基因組合,輸入一堆人類的基因資料,經過無監督的學習,可能會輸出通過某些基因因子來劃分的人類類別(cluster),而這在學習之前我們是無法知道的,甚至不知道應該由哪些基因因子來劃分人類
http://blog.csdn.net/bangemantou/article/details/12966533
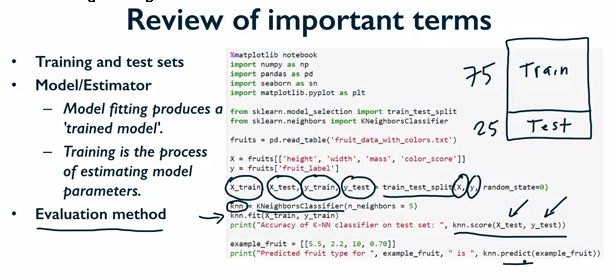
特徵,建模,模型,機器學習,訓練資料集
計算機用來學習的、反覆看的圖片叫“訓練資料集”;“訓練資料
集”中,一類資料區別於另一類資料的不同方面的屬性或特質,叫作“特徵”;計算機在“大
腦”中總結規律的過程,叫“建模”;計算機在“大腦”中總結出的規律,就是我們常說的“模
型”;而計算機通過反覆看圖,總結出規律,然後學會認字的過程,就叫“機器學 習”
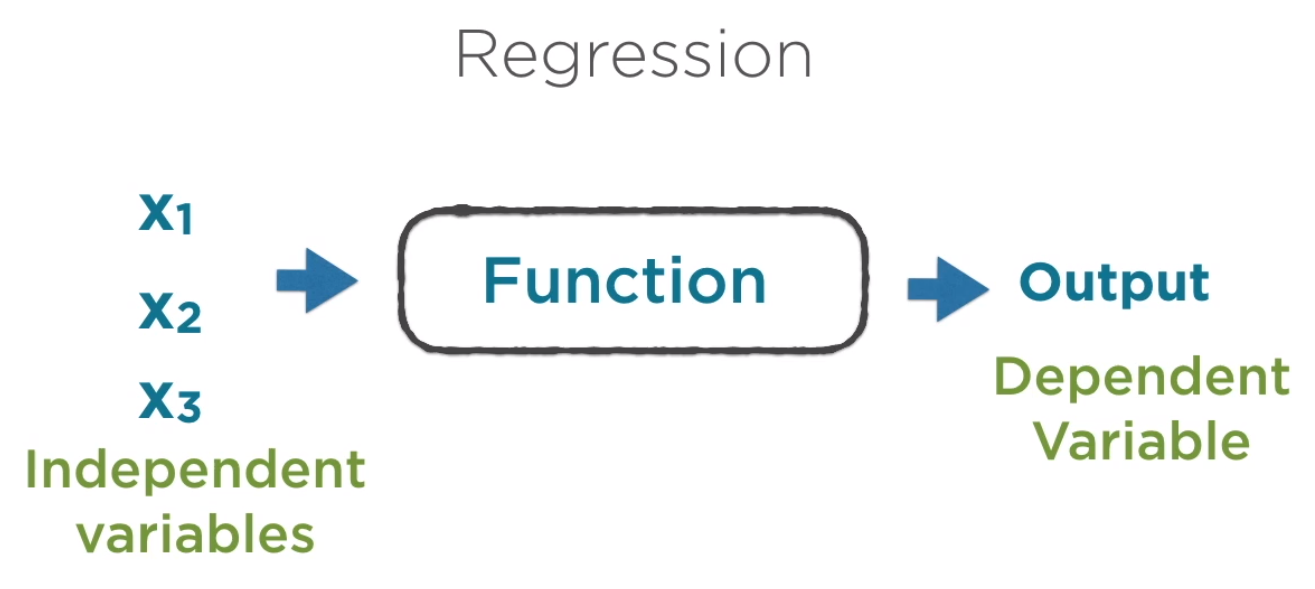
classification problem vs regression problem
分類問題輸出多個類別;regression problem輸出連續的預測值。
machine learning的一般性原理
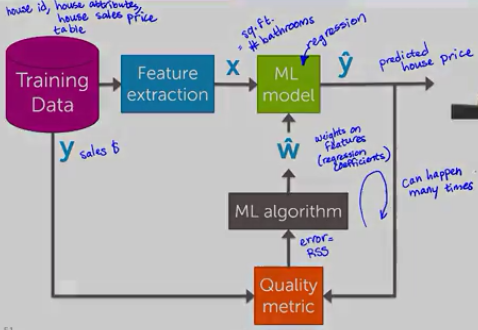
給定的training data set首先抽象出最重要的特徵引數,應用到一個機器學習model(比如regression model,神經網路),得出prediction。
將prediction和實際的y值按照一定規則做出預測誤差函式(w的函式),將該誤差函式(loss function)應用到機器學習演算法(比如梯度下降法)來優化模型model中的w引數,不斷優化使得quality(loss function)最小
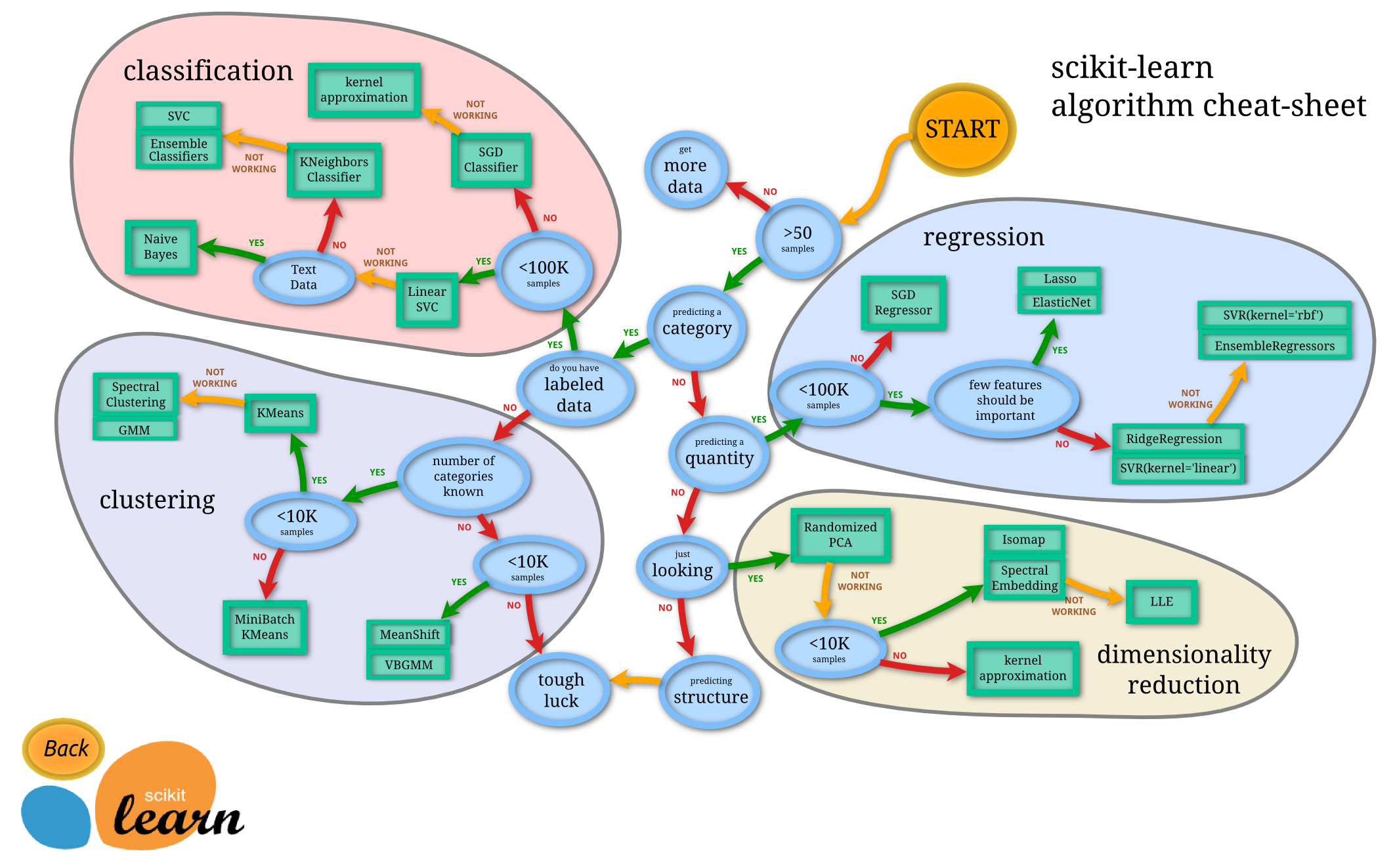
sk-learn學習模型演算法決策過程
http://scikit-learn.org/stable/tutorial/machine_learning_map/
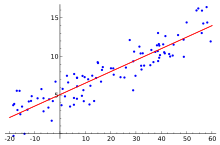
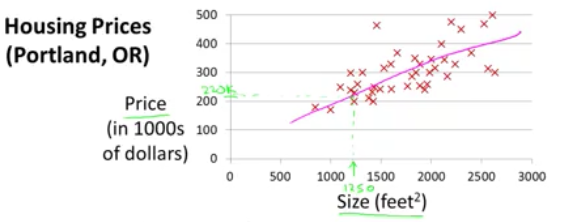
linear regression(線性迴歸)
給定一組資料x=[1,2,3,4,5]和y=[0.2,0,3,5,7]得出最能擬合x,y之間關係的一個線性曲線y=kx+b(這就是一元線性迴歸分析,因為只有一個自變數,一個因變數.如果迴歸分析中包括兩個或兩個以上的自變數,且自變數之間存線上性相關,則稱為多重線性迴歸分析),隨後我們據此曲線再給定任何一個資料,我們來預測其應有的輸出是多少(這就是regression問題的本質概念:預測一個連續的value)
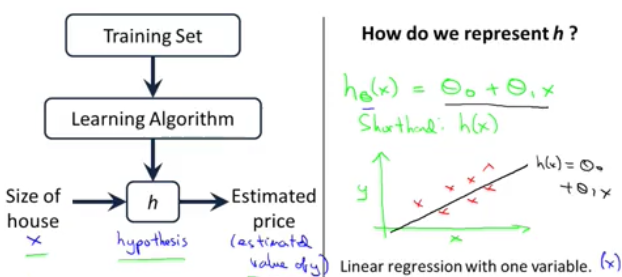
hypothesis(假設函式)(model)
線上性迴歸中,我們擬合出來的函式英文被成為hypothesis,也可以稱此函式為學習後建立的model,比如y=kx+b,其中k和b被稱為model的parameter,我們通過學習演算法針對training set來進行訓練學習,最終來確定這些parameter,從而就確定了最終的模型函式,通過這個函式,我們就可以做到對應的預測了
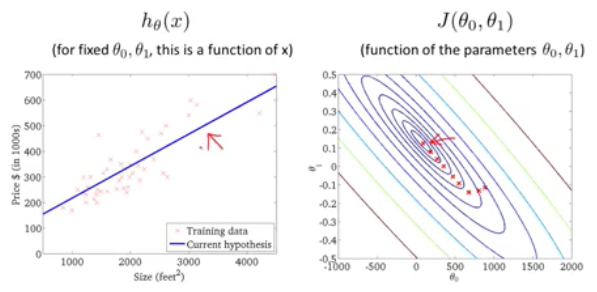
線性迴歸問題的目標(target)(objective): 找到最優的Θ0和Θ1兩個引數使得經過對於給定的training set中的x值,經過我們y=Θ0+Θ1X的hypothesis模型得到的預測值和真實值y之間的方差均值最小化,J(Θ0,Θ1)就被成為cost function(或者說目標函式),也就是說使得目標函式最小化是我們機器學習演算法的最終目標
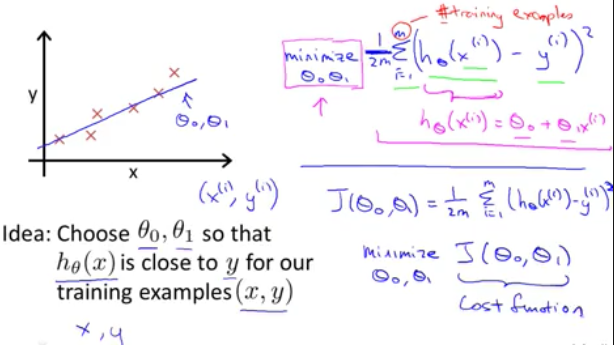
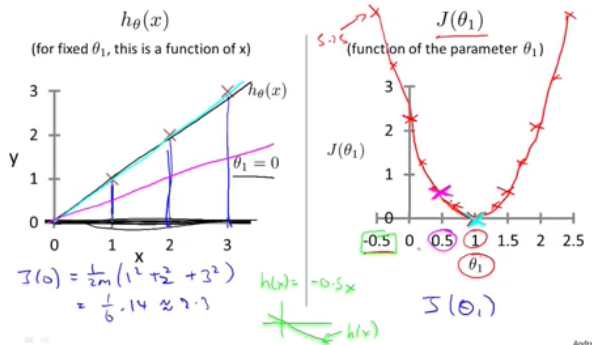
hypothesis和loss函式對比解讀(假設Θ0 = 0以便簡化問題), h函式為x的函式,而J函式則為Θ1的函式,我們選定不同的Θ1得到不同的h(x)函式,對應繪製圖形,可以看出在Θ1=1時,J(Θ1)達到最小值,也就在這時,h函式和輸入的訓練集完全擬合
gradient descent(梯度下降法)
注意在梯度下降法更新引數時,必須是一次性同時更新Θ0和Θ1引數,而不執行交錯更新!
梯度下降是優化loss function使得其最小化的演算法

convex fuction(凸函式)
線性迴歸的Loss函式是一個凸函式(相一個碗一樣),只有一個全域性最底點
Matrix inverse
如果A是一個mXm的矩陣,如果它有逆矩陣,則:
A*A-1 = A-1 *A = I
I = [
1 0
0 1
]的單位矩陣
singular matrix:不可逆的矩陣
矩陣相乘

通過矩陣相乘,來實現一次批量計算多個假設函式(hypothesis)的預測值,而一般的library對於矩陣相乘都做了重要的優化,甚至可以完全發揮處理器多核,或者協處理器,高效地完成演算法執行工作。
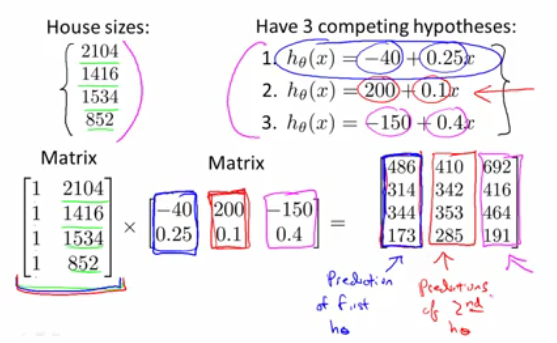
矩陣相乘的幾個特性:
A*B一般不等於B*A 不具有交換律
A*I = I* A(注意這裡的I的型是不同的緯度不同)

A*B*C=A*(B*C) 適用結合律
多元線性迴歸
如果輸入的feature有多個的話,這時線性迴歸問題就被稱為多元迴歸了,其hypothesis函式就可以簡化為矩陣表達方式: hθ(x)=θTX, 具體如下:
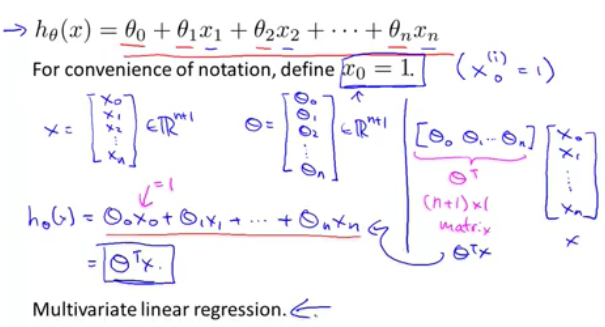
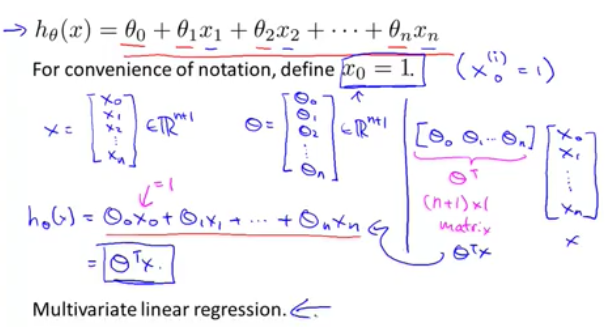
多元線性迴歸引數θ的更新(注意使用了新的下標表示不同feature(x)):

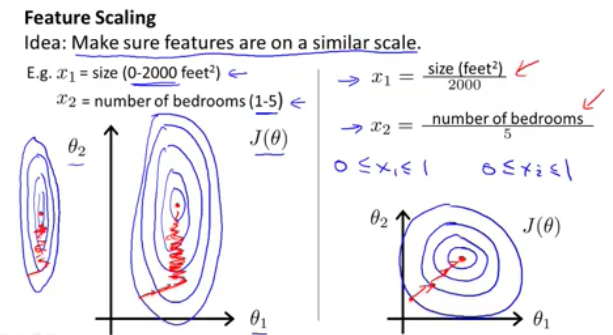
feature scaling的重要性:
我們在做線性迴歸梯度下降演算法時,如果多個引數的輸入引數(feature)值範圍相差巨大,則會導致收斂速度過慢,因此我們在訓練資料時,首先需要做的是輸入訓練資料的正規化,常用的方法是mean normalization減去均值除以範圍

學習率α的重要性
如果過大,可能導致迴歸發散,如果過小則會導致收斂過慢。可以在實驗中畫出J(θ) 對於iteration number的函式影像
多元迴歸的部分notation圖例
hypothes = 引數向量*feature向量(x)

linear regression梯度下降法的替代方案(矩陣轉置直接求解法)
梯度下降法對於求解θ引數使得cost function最小化是一個通用方法,但是如果x feature個數很少的話,我們有一個替代方案,無需梯度下降無數步的迭代,一次性計算即可得出θ引數

矩陣不可逆的幾種原因及其解決方案

為何一般矩陣向量都會預設寫成列向量?
原因在於一般矩陣都對應著線性對映,考慮矩陣A,如果x是列向量,那麼不妨把A對應的線性對映還是記作A,那麼就有A(x)=Ax,右邊就是矩陣的乘法.A(x)=Ax
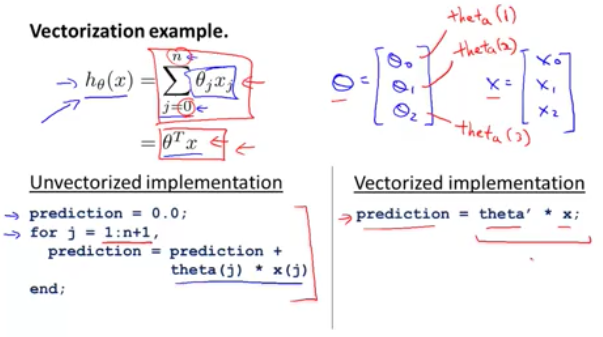
矩陣內積的矩陣向量化求解
我們知道對於線性迴歸的h函式表示為h=θ0+θ1x1+θ2x2,如果要求解特定引數下的h值,我們編碼有兩種方案,要麼for loop來求解,要麼通過矩陣運算來求解。要使用矩陣運算,首先第一步我們就要將x和θ做向量化,這樣矩陣運算的好處是會運用到科學計算中已經優化的庫程式碼,甚至很好地運用到並行處理
Logistic Regression Classification
對訓練集訓練後,輸出(0,1),表徵結果的分類。這時如果使用線性迴歸演算法並不適合,這時我們就要使用新的演算法:邏輯迴歸。
在邏輯迴歸分類演算法中,由於輸出必須在0到1之間,因此我們要引入一個叫做sigmoid函式(或者稱為logistic function)來對θTx做轉換
hθ(x)=P(y=1|x;θ) 給定features x,在引數為θ的情形下,輸出y=1的概率值,在邏輯迴歸演算法中,所有的概率加起來必須為1,比如:
P(y=1|x;θ)+P(y=0|x;θ) = 1
decision boundary
決策邊界只取決於給定的θ引數,和訓練資料集無關,使用高階多項式外加sigmoid函式組成hypothesis函式,則可以形成非常複雜的決策邊界

獲取訓練資料的幾個方法
1. 人工合成,比如使用已有的字型庫,就可以獲得大量字元不同形態的image,或者對已有的資料做變形處理,比如可以對圖片做傾斜,拉伸等操作形成新的labled data set
2.自己來做蒐集標註整理
3. 僱傭人工標註, https://www.mturk.com/mturk/welcome
基於tensorflow機器學習應用開發和部署流程
http://blog.csdn.net/qq_36510261/article/details/72533550
推薦系統
http://blog.csdn.net/initphp/article/details/52368867
terms used in machine learning
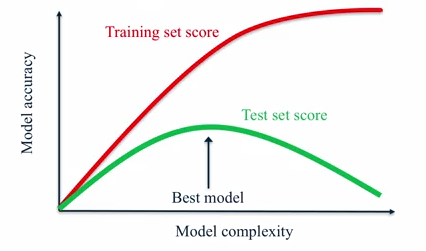
model accuracy vs model complexity
從下面的圖中可以看到隨著model複雜度增加,針對training set,模型可以完美地擬合(fit),但是對於test set卻並不是持續增加的!我們必須尋找到一個平衡點,
使得我們的model既能比較好的擬合訓練集,又能很好的generalize(泛化),也就是真正學到了global pattern,而不是僅僅為了擬合一些noise data(local pattern)而過擬合
generization泛化/過擬合/欠擬合(overfitting/underfitting)概念

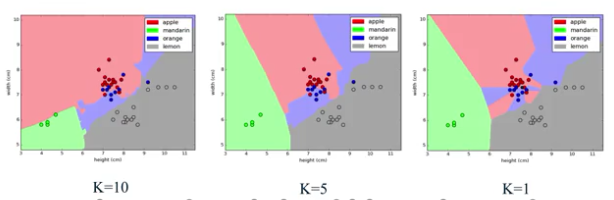
理解,檢測,並且避免overfitting或許是機器學習中需要解決的最重要的問題
simple models is much more effective at ignoring minor variations in training data and capturing the more important global trend with better generization performance
處理overfit的幾種思路:
1. 減少不必要的特徵feature參與運算
2.大量增加有效的資料
3.通過正規懲罰項來均勻化各個特徵對y的貢獻

機器學習的一般過程:
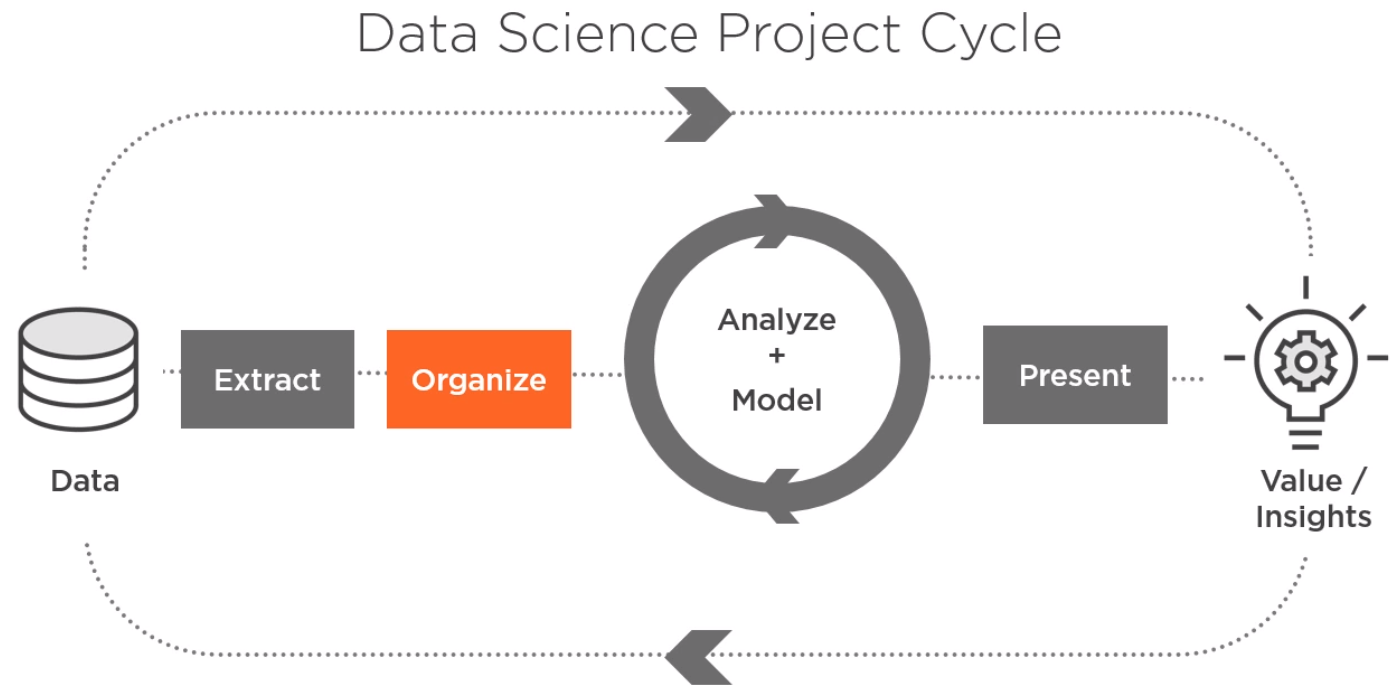
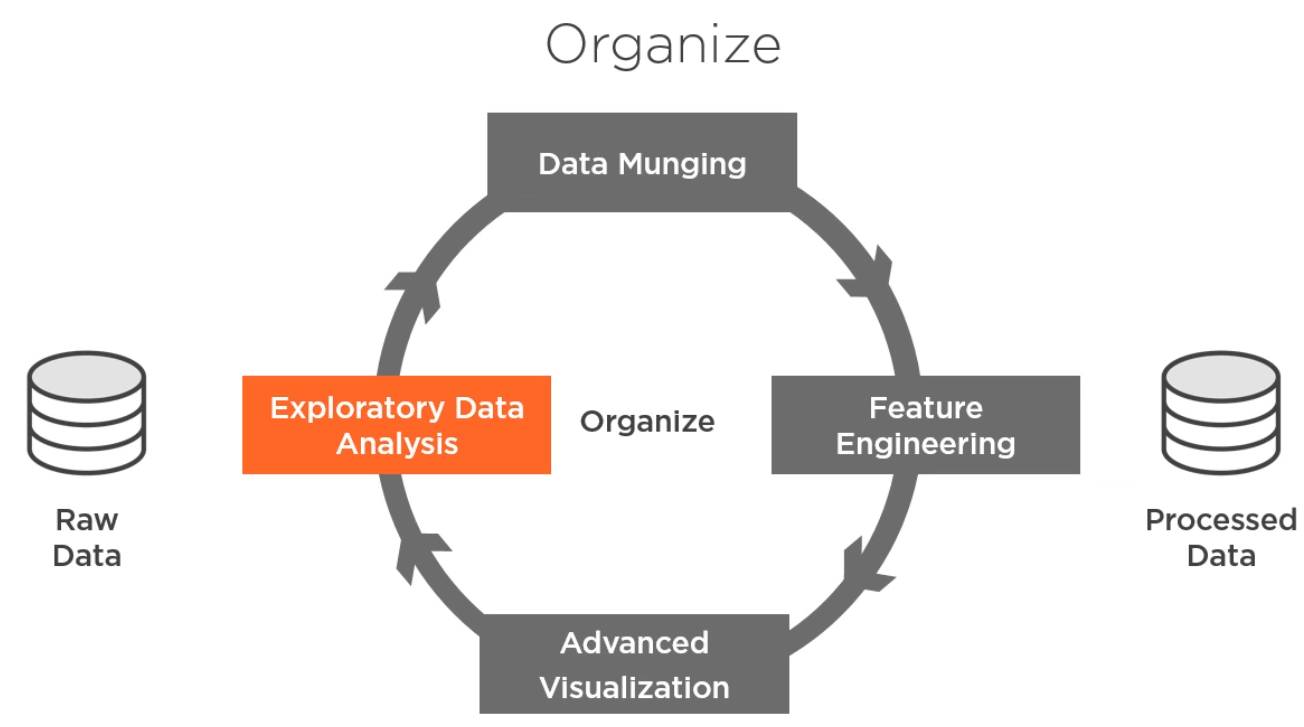
資料組織和資料清洗中用到的引數
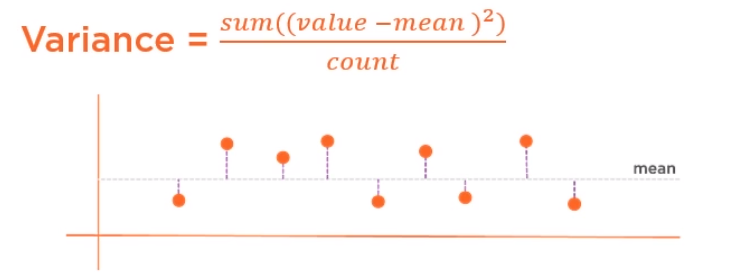
variance: (真值-均數)的平方取和除以count
standard variance:取variance的根號


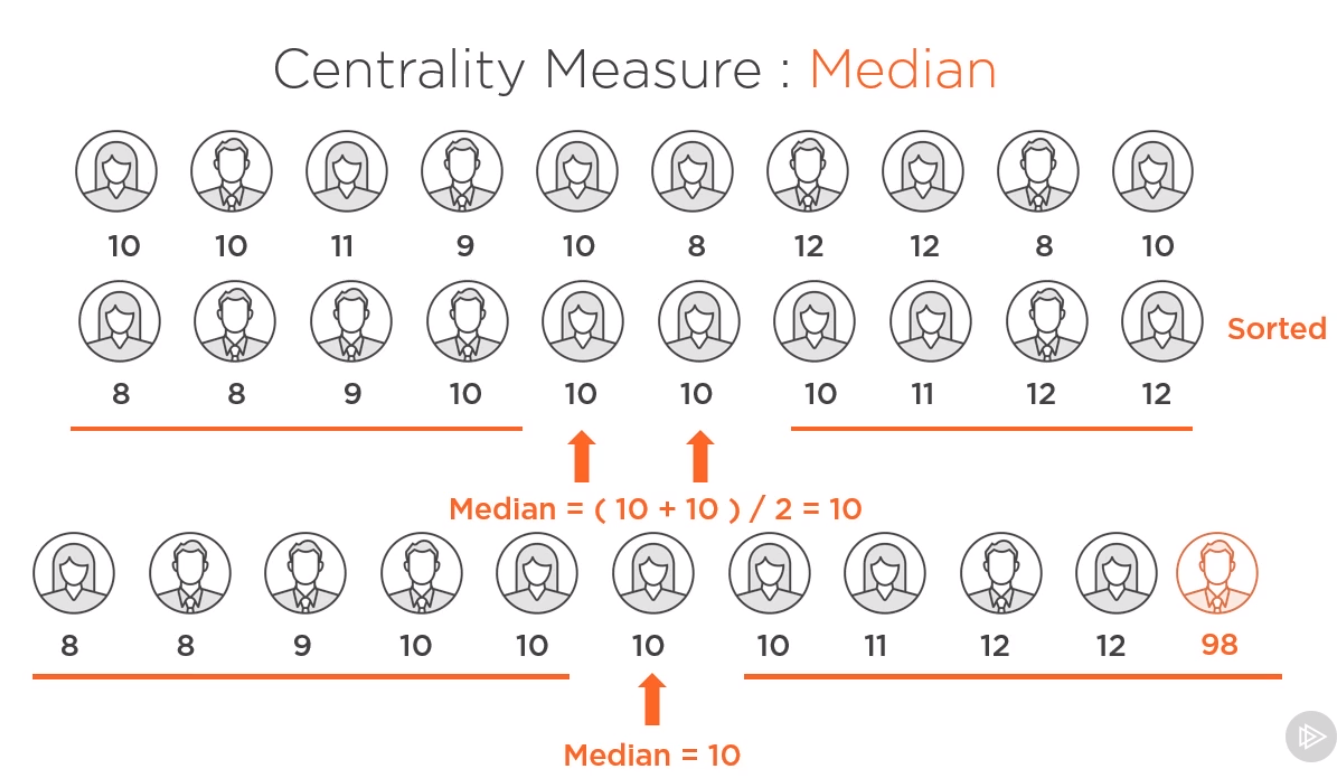
數值量:
- 中點度量(mean,median)
-資料分散性度量 (range,percentile, variance, standard deviation)
類別量:
- top count
- unique count
-category counts and proportions
per category statistics

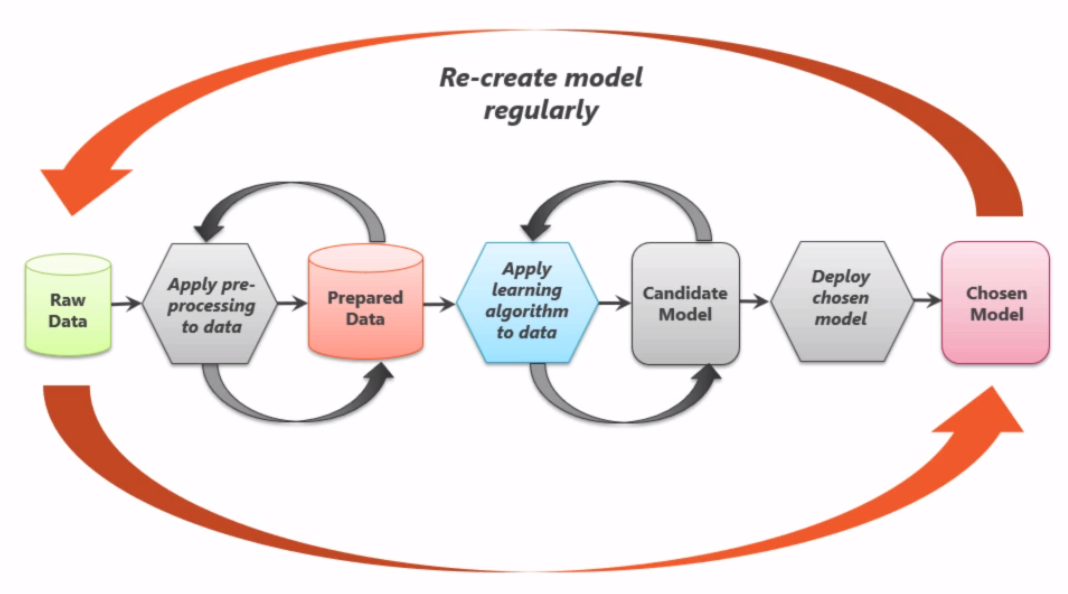

機器學習model的生命週期
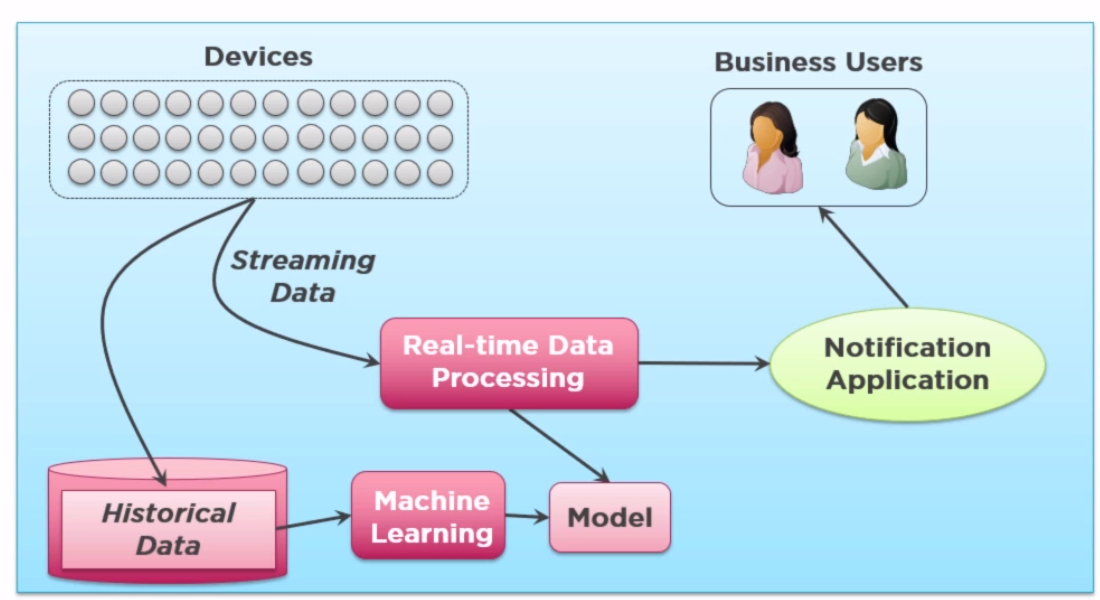
機器學習研究方法過程


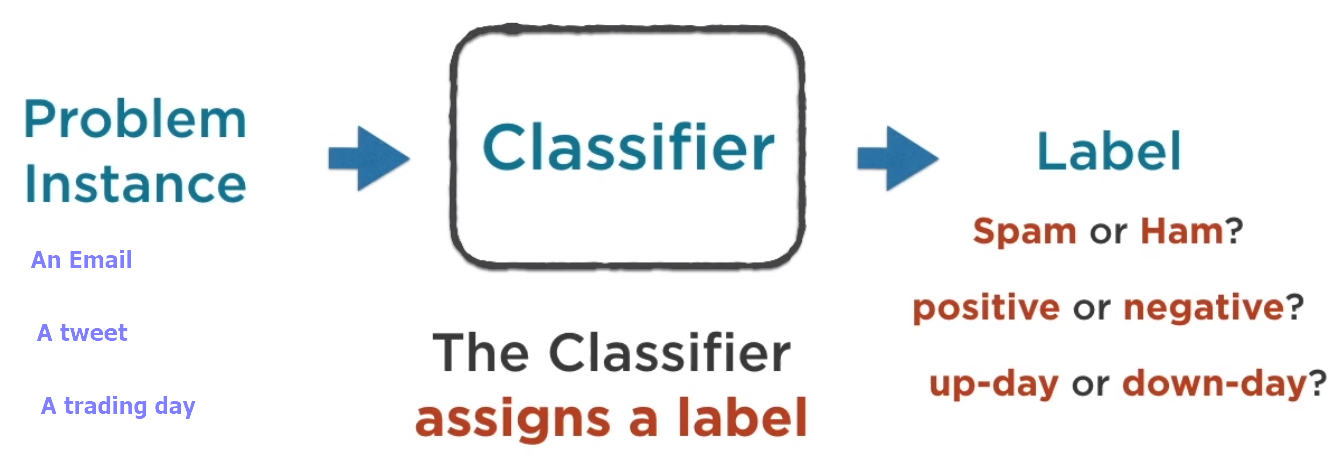
機器學習問題分類

神經網路相關:


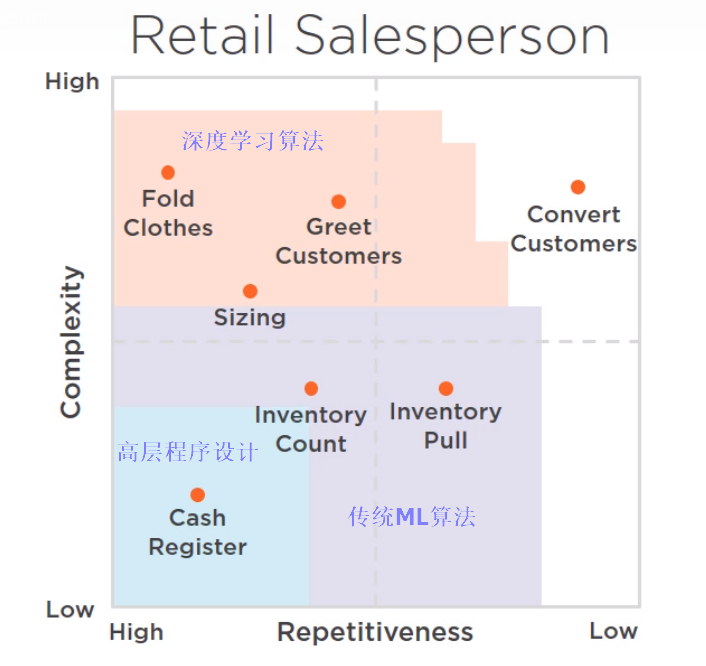
人工智慧可以涉足的領域:複雜度和重複係數
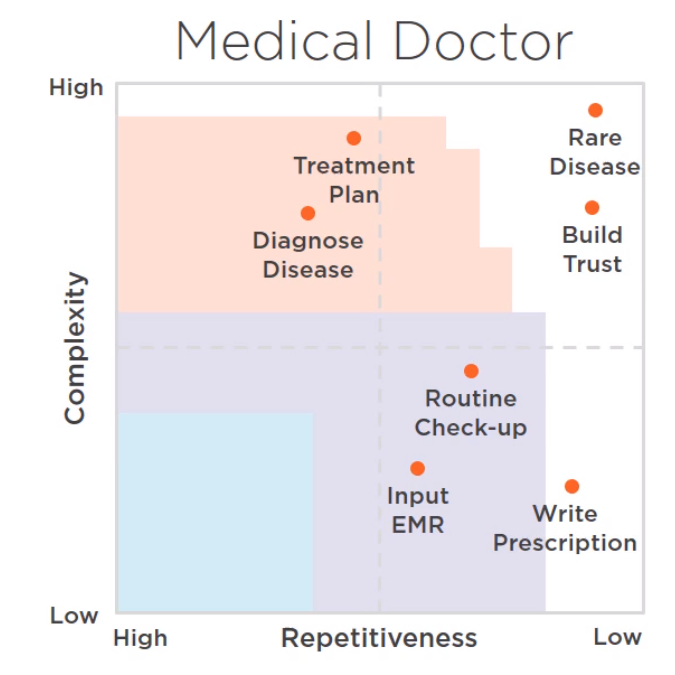
如何知道哪些features是predictive的,我們如何選擇一個學習的演算法?
資料科學家的重要工作就是做特徵選擇