機器學習——邊角料

演算法設計的一大原則

sigmoid型函式

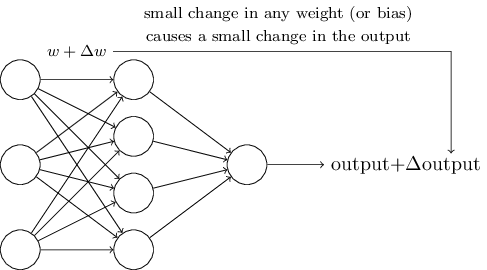
注意一點，在神經網路引入sigmoid型函式的目的是避免，對權重一個微小的改變可能對輸出帶來的顯著的改變，這一情況的發生（以此我們來進行微調）。σ(⋅)完美地將整個實數域的值對映到(0,1)區間（對應著概率probability？）。

何謂向量化一個函式（vectorizing a function ）

也即是將函式作用於向量中的每一個元素得到的輸出再組合成一個向量。舉例說明：

其中w是一個二階權值矩陣（代表前後兩個layer中的神經元之間的權重），a是一個向量（表示前一層每一個神經元的輸出組成的向量），b表示上一層向下一層的偏置，σ(⋅)是sigmoid型函式。

def sigmoid(z):
return 1/(1+np.exp(-z))
# 此時sigmoid接收的是一個向量，sigmoid(z)的做法正是一種vectorize 的做法
a = sigmoid(w.dot(a)+b)


1. 單層神經網路的增廣（augmentation）形式

   
   
   
   z=w1x1+w2x2+…+wdxdϕ(z)={0ifz≤θ1ifz>θ
   \begin{equation} z=w_1x_1+w_2x_2+\ldots+w_dx_d\\ \phi(z)=\left \{ \begin{array}{l} 0\qquad if \quad z \leq \theta\\ 1\qquad if \quad z > \theta \end{array} \right. \end{equation}

   為了形式的簡單和統一，可將上式轉換如下形式：
   

   z′===−θ+w1x1+w2x2+…+wdxdw0x0+w1x1+…+wdxdwTx
   \begin{equation} \begin{split} z'=&-\theta+w_1x_1+w_2x_2+\ldots+w_dx_d\\ =&w_0x_0+w_1x_1+\ldots+w_dx_d\\ =&w^Tx \end{split} \end{equation}

   也即是：

   ⎛⎝⎜⎜⎜⎜x1x2⋮xd⎞⎠⎟⎟⎟⎟d⇒⎛⎝⎜⎜⎜⎜⎜⎜⎜x0x1x2⋮xd⎞⎠⎟⎟⎟⎟⎟⎟⎟d+1
   \begin{equation} \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_d \end{pmatrix}_d\Rightarrow \begin{pmatrix} x_0\\ x_1\\ x_2\\ \vdots\\ x_d \end{pmatrix}_{d+1} \end{equation}
   ⎛⎝⎜⎜⎜⎜w1w2⋮wd⎞⎠⎟⎟⎟⎟d⇒⎛⎝⎜⎜⎜⎜w0w1⋮wd⎞⎠⎟⎟⎟⎟d+1
   \begin{equation} \begin{pmatrix} w_1\\ w_2\\ \vdots\\ w_d \end{pmatrix}_d\Rightarrow \begin{pmatrix} w_0\\ w_1\\ \vdots\\ w_d \end{pmatrix}_{d+1} \end{equation}
   ϕ(z′)={0ifz′≤θ1ifz′>θ
   \begin{equation} \phi(z')=\left \{ \begin{array}{l} 0\qquad if \quad z'\leq\theta\\ 1\qquad if \quad z'>\theta \end{array} \right. \end{equation}

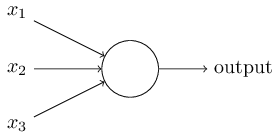
   轉換後的形式是原來形式的增廣形式，即分別對特徵向量x

   x
   和權值向量做一維的增廣，w0=−θ,x0=1
   w_0=-\theta, x_0=1

2. neuron單輸出還是多輸出？

   答案是單輸出（single output）
   

   
   
   
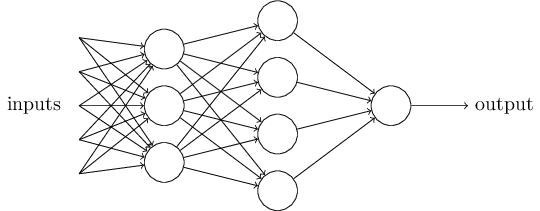
   通常我們看到的關於多層感知機（perceptron）網路的圖示如上圖。然而，這樣的圖有一種“迷惑性的”一點是，對於每一個神經元節點（neuron）而言，它們都是多輸入和單輸出，雖然從一個神經元出來的箭頭指向下一層的每一個節點，其實輸出的每一個值都是相等的，這樣做只是出於一個直觀的需要。

3. 人工神經元從perceptron到sigmoid neuron

   
   
   

   引入sigmoid neuron（S型神經元）的目的是避免對權值（w1,…,wd

   w_1,\ldots, w_d
   ）或者偏置（bias，w0
   w_0
   ）的小幅修改可能對最終的輸出造成的比較大的變化，比如分類問題中，將-1判斷為1，手寫識別例子中將8錯分為9。
   
   z=wTxσ(z)=11+e−z
   \begin{split} &z=w^Tx\\ &\sigma(z)=\frac{1}{1+e^{-z}} \end{split}
   
   σ(⋅)
   \sigma(\cdot)
   實現了原始輸入(−∞,∞)
   (-\infty, \,\infty)
   向(0,1)
   (0, \,1)
   的對映（map），實現了一種值域的收縮，也可實現降低輸入（weigts、bias）的小幅修改對輸出可能造成的影響，如此我們可放心地調整引數，實現更優的結果，而不會出現，因輸入的變化可能造成的結果的跳變。