LeetCode解題報告 120. Triangle [medium]
題目描述
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 =
11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
解題思路
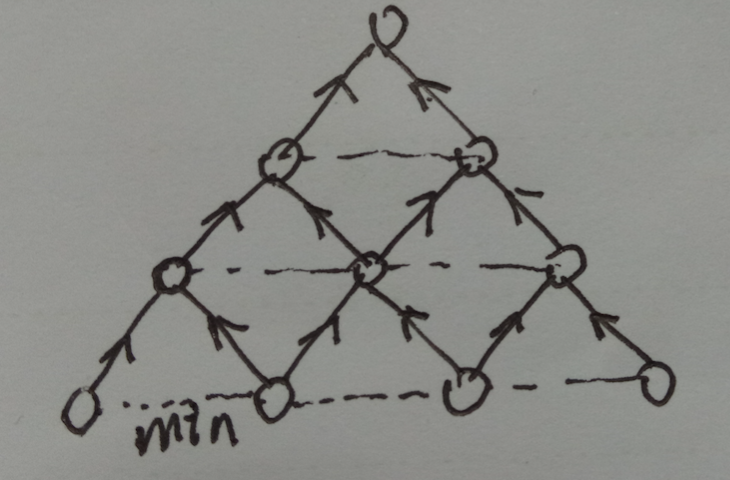
採用由底向上傳輸的思路,在每兩層之間找到最小值,不斷向上傳遞並相加,最後頂點的值儲存的就是所求的最小值。
對於從倒數第二層開始的每個點,可選擇從左下方的點或者從右下方的點走這條最終的最短路,因此比較左右下方的兩個結點,取最小值,再加上自己本身,就是這個小三角形區域的最短路。對倒數第二層的每一個結點都做同樣的操作,每個結點都儲存的是自己所在的小三角形的最短路的和。然後依次計算倒數第三層...,直到最頂點。
狀態轉移方程如下:
tra[i][j]=tra[i][j]+min(tra[i+1][j+1], tra[i+1][j])
return tra[0][0]
圖示如下:
複雜度分析
O(n*n)的時間複雜度。
程式碼如下:
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int n=triangle.size();
if (n==0) {
return 0;
}
else if (n==1) {
return triangle[0][0];
}
else{
for (int i = n-2; i>=0;--i)
{
for (int j=0; j<=i; j++) {
triangle[i][j]+=min(triangle[i+1][j],triangle[i+1][j+1]);
}
}
return triangle[0][0];
}
}
};相關文章
- [LeetCode] 120. TriangleLeetCode
- Leetcode 120. TriangleLeetCode
- LeetCode解題報告 279. Perfect Squares [medium]LeetCode
- LeetCode解題報告 241. Different Ways to Add Parentheses [medium]LeetCode
- LeetCode解題報告 452. Minimum Number of Arrows to Burst Balloons [medium]LeetCode
- LeetCode解題報告 108. Convert Sorted Array to Binary Search Tree [medium]LeetCode
- Leetcode 第136場周賽解題報告LeetCode
- LeetCode Weekly Contest 96 解題報告LeetCode
- Leetcode Weekly Contest 95解題報告LeetCode
- Leetcode TriangleLeetCode
- Leetcode Weekly Contest94 解題報告LeetCode
- [leetcode] 252. Meeting Rooms 解題報告LeetCodeOOM
- Leetcode-TriangleLeetCode
- Triangle leetcode javaLeetCodeJava
- LeetCode 解題報告 - 2. Add Two NumbersLeetCode
- [Leetcode] 253. Meeting Rooms II 解題報告LeetCodeOOM
- Leetcode Pascal's TriangleLeetCode
- Doris建立表報錯Failed to find enough host with storage medium問題解決AI
- 【LeetCode】253. Meeting Rooms II 解題報告(C++)LeetCodeOOMC++
- LeetCode 120 TriangleLeetCode
- leetcode Pascal's Triangle IILeetCode
- Leetcode-Pascal's TriangleLeetCode
- [熵值] 解題報告熵
- 【LeetCode】 Best Time to Buy and Sell Stock I II III IV 解題報告LeetCode
- Leetcode-Pascal's Triangle IILeetCode
- Pascal's Triangle II Leetcode javaLeetCodeJava
- Leetcode-Medium 621. Task SchedulerLeetCode
- LeetCode - Medium - 322. Coin ChangeLeetCode
- ARC173 解題報告
- CF1991F Triangle Formation 題解ORM
- 【LeetCode】416. Partition Equal Subset Sum 解題報告(Python & C++)LeetCodePythonC++
- LeetCode解題報告 102. Binary Tree Level Order Traversal [easy]LeetCode
- 【LeetCode】455. Assign Cookies 分發餅乾(Medium)(JAVA)每日一題LeetCodeCookieJava每日一題
- Leetcode 611 javascript Valid Triangle NumberLeetCodeJavaScript
- [LeetCode 刷題] 3. 無重複字元的最長子串 (Medium)LeetCode字元
- LeetCode 207. 課程表(Medium)LeetCode
- LeetCode - Medium - 11. Container With Most WaterLeetCodeAI
- CF720B 解題報告