IV.3 計算數論

黃志斌發表於2014-12-06
第二卷：2014年1月第一版，2014年4月第二次印刷
頁 段 行 原文 擬改為 備註
60 2 4 所以 7 是一個素數 1 所以 7 是一個素數
60 注① 3～4 古代的印度數學家和伊斯蘭的數學家就已經知道了這個定理. 刪除
63 -1 4 二項定理 二項式定理
63 -1 5 二項定理 二項式定理
64 1 3 二項定理 二項式定理
65 -1 3 Starassen Strassen
66 -1 1 （來自 Kraitchik （基於 Kraitchik
67 2 6 素因子 13， 素因子 23，
69 2 -2 左右的合數，或者對於沒有 左右的沒有
69 注① -4 327691 × 327691
70 -1 1 取整數 x,y,a, 取整數 x1,y1,a,
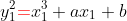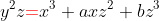70 -1 1 IV.3 計算數論 IV.3 計算數論
71 2 2 IV.3 計算數論 IV.3 計算數論
71 -1 3 在黎曼 ς 函式 ς(s) 在黎曼 ζ 函式 ζ(s)
71 -1 4～5 ς(s) 的級數只當 ζ(s) 的級數只當
71 -1 -4 通過恆等式 ς(s) = s/(s-1) 通過恆等式 ζ(s) = s/(s-1)
71 -1 -2 ς(s) 可以擴充為 ζ(s) 可以擴充為
72 1 1 ς(s) ≠ 0 ζ(s) ≠ 0
72 2 -4 Meiser Meissel
72 -2 -3 Crandle Crandall
72 -1 1 與 ς 函式的零點位置 與 ζ 函式的零點位置
72 -1 2 把 ς 函式的平凡的零點 把 ζ 函式的平凡的零點
72 -1 2 即位於偶整數 即位於負偶整數
72 -1 -1 黎曼 ς 函式的零點 黎曼 ζ 函式的非平凡零點
73 1 1 函式方程 ς(1-s) 函式方程 ζ(1-s)
73 1 1 Γ(s)ς(s) Γ(s)ζ(s)
73 2 4 IV.3 計算數論 刪除紅色部分
73 2 5 定義 Λ(n) = p 定義 Λ(n) = log p
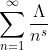73 2 7 IV.3 計算數論 IV.3 計算數論
73 2 -7 與 ς'/ς 在極點處的 與 ζ'/ζ 在極點處的
73 2 -7 相應於 ς 函式的零點 相應於 ζ 函式的零點
73 2 -4 而對 ς 函式的零點 而對 ζ 函式的零點
73 2 -3 即要求 |Imρ| < T 即要求 |Im(ρ)| < T cf. p74 line13
73 2 -2 是與 ς 函式的 是與 ζ 函式的
74 1 1 ς(s) 有一些非平凡的零點 ζ(s) 有一些非平凡的零點
74 1 11 為了確定複函式 ς(s) 的零點 為了確定複函式 ζ(s) 的零點
74 1 12 IV.3 計算數論 IV.3 計算數論
74 1 12 ς 函式 ζ 函式
74 1 -5 ς 函式 ζ 函式
74 2 1 ς 函式 ζ 函式
74 2 2 ς 函式 ζ 函式
74 2 3 ς 函式 ζ 函式
74 2 -1 ς 函式 ζ 函式
74 -2 1 ς 函式 ζ 函式
74 -2 3～4 ς 函式 ζ 函式
74 -1 -1 ς 函式 ζ 函式
75 2 1 ς 函式 ζ 函式
75 3 -2 ς 函式 ζ 函式
75 4 1 ς 函式 ζ 函式
76 1 2 虛部在 1.3 × 1023 左右 虛部在 1.3 × 1022 左右
76 2 1 ς 函式 ζ 函式
76 2 -3 ς 函式 ζ 函式
76 -3 -3 有助於開闢了代理數理論 有助於開闢代理數理論
77 2 8 本身也在 R. 本身也在 R 中.
77 -2 -2 正整數 x,y,x,u,v,w 滿足 正整數 x,y,z,u,v,w 滿足
78 -3 6 1n + 22 = 32 1n + 23 = 32
78 -3 9 27 + 173 = 172 27 + 173 = 712
80 2 3 unicaen.fr/-nitaj/abc.html unicaen.fr/~nitaj/abc.html
81 4 2 孿生素數猜測 孿生素數猜想

相關文章