Bagging和RandomForest學習

其實Bagging和隨機森林的思想都是可以普適性的用在其他的分類器上的，思想其實都是可以通用的，只不過有的合適有的不合適而已，決策樹就是一種比較合適用Bagging和隨機森林來提升的分類器之一。

Bagging

BootStrap Aggregation：從樣本中重取樣(有重複的)選出n個樣本，在所有的屬性上，對這n個樣本建立分類器(ID3、C4.5、CART、SVM、Logistic迴歸等)。
重複上述步驟m次，得到m個分類器，將所有資料放在這m個分類器上，最後根據這m個分類器的投票結果決定屬於哪一類。

有論文證明，BootStrap 取樣，大約會有63%是不重複的：

裡邊的具體證明我們就不管了，知道這麼個事情就可以了。

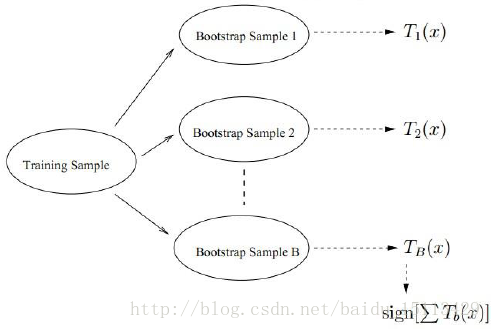
這幅圖是說明了Bagging的這個過程以及投票。

隨機森林

隨機森林在Bagging的基礎上做了修改：
(1): 從樣本中用BootStrap 取樣了n個樣本。
(2): 從所有屬性中隨機選擇K個屬性，選擇最佳分割屬性作為結點建立CART決策樹。
(3): 重複上邊2步m次，即建立m棵CART決策樹。
(4): 這m棵CART樹形成隨機森林，通過投票表決結果屬於哪一類。

我們介紹的是使用決策樹作為基本分類器，當然也可以是別的分類器。

當然了，除了分類問題，迴歸問題也可以嘗試使用：

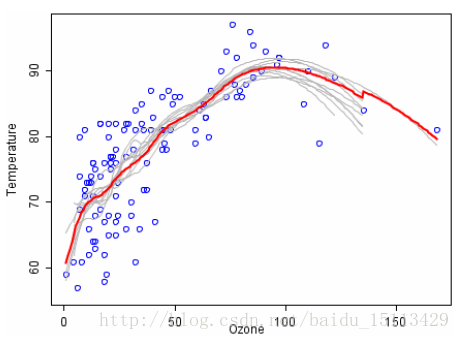
顯然紅色曲線基本上優於每一條灰色的，其實紅色曲線就是灰色曲線取平均得來的，這樣的紅色曲線是比較穩定的並且不容易過擬合。

最後介紹一下投票機制，可能你會覺得投票還不簡單，少數服從多數唄，此言差矣啊。

簡單投票機制：

(1): 一票否決
(2): 少數服從多數（可以加權）
(3): 閾值表決（就像美國選總統那樣，但是Trump還是贏了）

貝葉斯投票機制：

假定有N個使用者可以為X個電影投票(假設某位投票者不可對同一電影重複投票)，投票有1，2，3，4，5個檔。
根據使用者投票可以對電影排序：
本質是分類問題，對於某電影，有N個決策樹，每棵樹對電影有一個分類(1,2,3,4,5)，求這電影屬於哪一類？（如果可以是小數，就變成了迴歸問題）

一種可能：

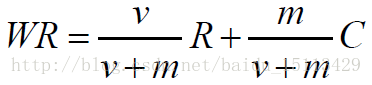
WR：加權得分(weighted rating)
R： 該電影的使用者投票的平均得分(Rating)
C： 所有電影的平均得分
v： 該電影的投票人數(votes)
m： 排名前250名電影的最低投票數
我們現在來分析一下這個公式，假設現在有一個電影，沒人投票，那麼也就是v = 0，那麼也就是說該電影的得分就是所有電影的平均分。假設m這個超引數是0，那麼也就是說最後的得分就是使用者的投票啊。
還是很有道理的吧，還是很喜歡貝葉斯思維的。