經典面試題（四）附答案 演算法+資料結構+程式碼 微軟Microsoft、谷歌Google、百度、騰訊

yangxi_001發表於2014-06-13
面試題演算法資料結構微軟ROS谷歌Go

1金幣概率問題（威盛筆試題）

題目：個房間裡放著隨機數量的金幣。每個房間只能進入一次，並只能在一個房間中拿金幣。一個人採取如下策略：前四個房間只看不拿。隨後的房間只要看到比前四個房間都多的金幣數，就拿。否則就拿最後一個房間的金幣。程式設計計算這種策略拿到最多金幣的概率。

 

        這題真要用數學的方法計算，估計還真不好算。還好，題目要求用程式設計實現。這樣它就成了一個模擬題，即用程式來模擬整個取金幣的過程。

我們可以進行很多次實驗（如10000次）。每次實驗，對每個房間產生隨機數量的金幣數，然後按照題目中的策略拿金幣。如果拿到的金幣數恰好是最多的則成功。最後統計很多次實驗中成功的次數，並計算概率。

[cpp] view plaincopy
  1. #include <iostream>  
  2. #include <ctime>  
  3. using namespace std;  
  4.   
  5. const int MAX_COIN = 100;  
  6. const int MIN_COIN = 1;  
  7.   
  8. //初始化隨機數種子  
  9. void InitRandom()  
  10. {  
  11.     srand( time( NULL ) );  
  12. }  
  13.   
  14. //為每個房間產生隨機數量的金幣  
  15. int GegenrateGoldCoin( int *goldCoin, int size )  
  16. {  
  17.     int max = 0;  
  18.     for( int i=0; i<size; i++ )  
  19.     {  
  20.         goldCoin[i] = ( rand()%( MAX_COIN - MIN_COIN + 1) ) + MIN_COIN;  
  21.         if( goldCoin[i] > max )  max = goldCoin[i];  
  22.     }  
  23.     //範圍最多的金幣數  
  24.     return max;  
  25. }  
  26.   
  27. //按照給定的策略從房間中拿金幣  
  28. int TakeCoin( int *goldCoin, int size )  
  29. {  
  30.     int firstFour[4];  
  31.     int maxInFirstFour = 0;  
  32.     for( int i=0; i<4; i++ )  
  33.     {  
  34.         firstFour[i] = goldCoin[i];  
  35.         if( goldCoin[i] > maxInFirstFour ) maxInFirstFour = goldCoin[i];  
  36.     }  
  37.   
  38.     for( int i=4; i<size; i++ )  
  39.     {  
  40.         //如果比前四個房間的金幣都多，則拿  
  41.         if( goldCoin[i] > maxInFirstFour ) return goldCoin[i];  
  42.     }  
  43.   
  44.     //拿最後一個房間的金幣  
  45.     return goldCoin[size-1];      
  46. }  
  47.   
  48.   
  49. int main()  
  50. {  
  51.     int goldCoin[10];  
  52.     int tryCnt = 10000;  
  53.     int successCnt = 0;  
  54.   
  55.     InitRandom();  
  56.     //總共進行tryCnt次實驗  
  57.     for( int i=0; i<tryCnt; i++ )  
  58.     {         
  59.         int max = GegenrateGoldCoin( goldCoin, 10 );  
  60.         int choose = TakeCoin( goldCoin, 10 );  
  61.   
  62.         if( max == choose ) successCnt++;  
  63.     }  
  64.     cout << successCnt * 1.0 / tryCnt << endl;  
  65.     return 0;  
  66. }  

2.找出陣列中唯一的重複元素

1-1000放在含有個元素的陣列中，只有唯一的一個元素值重複，其它均只出現一次．每個陣列元素只能訪問一次，設計一個演算法，將它找出來；不用輔助儲存空間，能否設計一個演算法實現？

 

設陣列為A[1001] = { a1, a2, …, a1001 }，重複的元素為x, 且 1 <= x <=1000。

SumA = 1+…+1000

SumB = a1 + … + a1001

所以，唯一重複的元素為：x = SumB – SumA

要注意的問題：

1. 唯一重複的元素。這點很重要，如果有不止一個重複的元素，要找出其中任意一個，就不會這麼簡單了。

2. 注意溢位的情況。和的範圍：（1+1000）*1000/2 ≈ 1000^2 ≈ 2^20。具體程式設計實現的時候，使用4位元組的int完全可以搞定。如果資料範圍很大，比如陣列中存放的元素[1, 2^40],此時和的範圍（1+2^40）*2^40/2 ≈ 2^80,遠遠超過了8位元組的long long的表示範圍，求和時顯然會溢位。

3.百度校園招聘的一道筆試題

題目大意如下：

一排N個正整數，其中最大值１Ｍ，且+1遞增，亂序排列。第一個不是最小的，把它換成-1，最小數為ａ且未知，求第一個被-1替換掉的數原來的值，並分析演算法複雜度。

 

同上一題基本相同。

設這一排數是A1、A2、A3、…、AN，這N個數分別是: a, a+1, a+2, …, a+n

被替換掉的數為X。

SumA = A1+A2+A3+…+AN

SumB =a+(a+1)+…+(a+n)

則 X + 1 = SumB – SumA

處理溢位情況：

和的最大範圍a + … + 2^20 ≈ 1+…+ 2^20 ≈ (1+2^20)* 2^20/2 =2^40。使用4位元組的int會溢位。

下面有種方法，可以進行一個簡單的處理，但處理能力有限。

使用輔助陣列data，陣列的元素是Ai-(a+i-1)。則data的所有元素之和恰好是SumB – SumA。現在要說明的是：對data的所有元素求和不會溢位。

最好情況下，這一排數{A1、A2、A3、…、AN}的順序基本和{ a, a+1, a+2, …, a+n }相同，這樣除了第一個元素，其餘元素對應相減都為0，因此不會溢位。

最壞情況下，{A1、A2、A3、…、AN}遞減排列，{ a, a+1, a+2, …, a+n }遞增排列。此時，data的前N/2個元素為正，後N/2個元素為負。相加求和時，只要前N/2個元素的和不溢位，則結果不溢位。這時，前N/2個元素分別為：

(a+n)-(a), (a+n-1)-(a+1), (a+n-2)-(a+2),…2, 0

則，前N/2個元素的和：(((a+n)-(a))*n/2)/2 = n^2/4≈(2^20)^2/4≈ 2^40

3.一道SPSS筆試題求解

題目：輸入四個點的座標，求證四個點是不是一個矩形

關鍵點：

1.相鄰兩邊斜率之積等於-1，

2.矩形邊與座標系平行的情況下，斜率無窮大不能用積判斷。

3.輸入四點可能不按順序，需要對四點排序。

 

演算法步驟：

1.首先，對這四個點按照x座標從小到大排序，設這四個點分別為A、B、C、D。

2. 如果A.x == B.x，即如果是矩形，則與座標軸平行。

即要求C.x == D.x&&( ( A.y == C.y && B.y == D.y ) || ( A.y == D.y && B.y== C.y ) )

3. 如果A.x != B.x，則計算四條邊的斜率Kab、Kac、Kdb、Kdc。如果是矩形，則有三個內角都為90度。

  即要求 Kab*Kac== -1 && Kdb*Kdc == -1 && Kac*Kdc == -1.

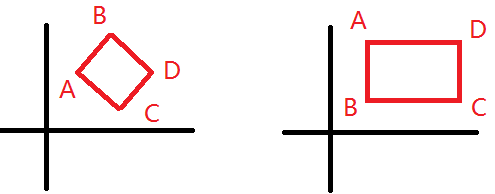
4.求兩個或N個數的最大公約數和最小公倍數。

 

        求兩個數的最大公約數，即gcd( a, b ) = ?。先不管最大公約數怎麼求，一旦已知最大公約數，就可以很容易得到最小公倍數。兩個數的最小公倍數 = a * b / gcd( a, b)

        最大公約數可以採用經典的輾轉相差法。設這兩個數分別是a和b, 且a > b.要證明輾轉相差法，即要證明 gcd( a, b ) = gcd( b, r )，其中r = a mod b

 

設 c = gcd( a, b )，即 a = mc, b = nc.

且r = a – tb = mc – tnc = ( m – tn ) c

因此，gcd( b, r ) = gcd( nc, ( m – tn ) c ) = gcd( n, ( m – tn ) ) * c

即，現在要證明gcd( n, ( m – tn ) ) * c = c

即，要證明n, ( m – tn )互為質數。

 

再用反證法。即n, ( m – tn )存在公約數d，且d != 1

設n = xd，m – tn =yd，則m = yd + tn = yd + txd = (y+tx)d

即n = xd，m = (y+tx)d, 故gcd( a, b ) = gcd( mc，nc ) = cd != c，故矛盾

所以n, ( m – tn )互為質數

即gcd( a, b ) = gcd( b, r ) 

[cpp] view plaincopy
  1. //求a、b的最大公約數  
  2. int GetGCD( int a, int b )  
  3. {     
  4.     if( a < b )   
  5.     {  
  6.         //交換a、b值  
  7.         a = a + b;  
  8.         b = a - b;  
  9.         a = a - b;  
  10.     }  
  11.   
  12.     //輾轉相除  
  13.     while( b > 0 )  
  14.     {  
  15.         int r = a % b;  
  16.         a = b;  
  17.         b = r;  
  18.     }  
  19.     return a;  
  20. }  

還有一個問題：如何求3個數的最大公約數、最小公倍數？

5.字串原地壓縮

題目描述：“eeeeeaaaff" 壓縮為 "e5a3f2"，請程式設計實現。

 

        多媒體壓縮裡的行程編碼。當大量字元連續重複出現時，壓縮效果驚人。程式設計實現比較簡單，統計重複的字元個數，然後把個數轉化為字串接在原字元之後。具體程式設計，見程式碼：用兩個計數指標i, j掃描字串。i始終指向字元的第一次出現，j指向字元的最後一次出現+1。至於int轉string，這裡使用stringstream
[cpp] view plaincopy
  1. //字串的原地壓縮，即行程編碼、遊程編碼  
  2. void StrCompress( char *original, char *cmpr )  
  3. {     
  4.     if( original == NULL )  
  5.     {  
  6.         cmpr = NULL;  
  7.         return;  
  8.     }  
  9.   
  10.     int cnt = 0;  
  11.     int i,j;  
  12.     for( i=0, j=0; *(original+j) != '\0';  )  
  13.     {         
  14.         //統計相同字元的個數  
  15.         while( *( original + i ) == *( original + j ) )  
  16.         {  
  17.             cnt++;  
  18.             j++;  
  19.         }  
  20.           
  21.         //複製字元  
  22.         *cmpr++ = *( original + i );  
  23.         //複製字元個數  
  24.         stringstream ss;  
  25.         ss << cnt;  
  26.         string strCnt;  
  27.         ss >> strCnt;  
  28.         const char *pcstr = strCnt.c_str();  
  29.         while( *pcstr != '\0' ) *cmpr++ = *pcstr++;           
  30.           
  31.         cnt = 0;  
  32.         i = j;                    
  33.     }  
  34.     *cmpr++ = '\0';  
  35. }  

6.字串匹配實現

請以兩種方法，回溯與不回溯演算法實現。

 

回溯法，即最基本的方法。演算法複雜度O( m * n )

設主串mainStr = { S0, S1, S2, …, Sm },

模式串matchStr = { T0, T1, T2, …, Tn };

當T[0]…T[j-1] == S[i-j]…S[i-1]，即模式串的前j個字元已經和主串匹配，當前要比較T[j]和S[i]是否相等？

如果T[j] == S[i], 則i++, j++,繼續比較下一個

如果T[j] != S[i], 則i要回溯，也就是i要退回到與j開始匹配時的下一個位置。同時j=0, 表示模式串從頭開始，重新匹配。

 

不回溯：即用KMP演算法。演算法複雜度O( m + n )。

在KMP中，如果T[j] != S[i]，則i保持不動（即，不回溯）。同時，j不用清零，而是向右滑動模式串，用T[k]和S[i]繼續匹配。

演算法的關鍵在於：模式串向右滑動多少？即K=？顯然，k的值應該儘可能的大，即儘可能的向右滑動。


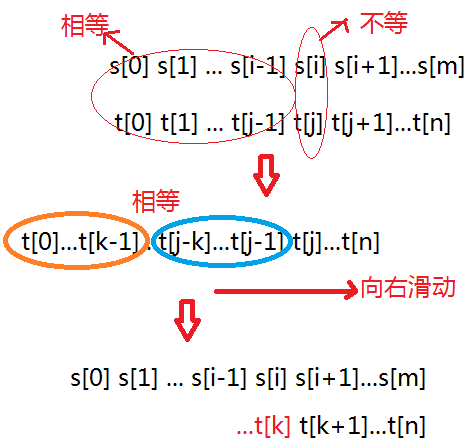
如圖，如果模式串T[0]...T[j-1]前後兩部分對稱，也就是T[0]…T[k-1] == T[j-k]…T[j-1],則模式串可以向右滑動k個距離，即用T[k]和S[i]繼續匹配。

因此 K = Max{ x | 0<=x<=j, 且T[0]…T[x-1] == T[j-x]…T[j-1]}

 

        由上面的分析可以對於任意的j，都對應一個k，於是我們把所有的K放到一個next陣列中。陣列元素next[j]=k，表示當T[j]匹配失敗時，下一次應該用T[k]繼續匹配。現在要解決的問題就是：如何求next陣列的值？當然，通過上面的理解，可以直接寫出簡單的字串的next，這裡我們的目標是給出一個求next的通用的方法。 

求next可以用一個遞迴的過程。已知next[j] = k, 求next[j+1] = ?

如果T[j] == T[k]，則next[j+1] = k+1

如果T[j] != T[k]，則next[j+1] = ?。

這時就相當於用T[k]去匹配T[j]，且匹配失敗。那麼，我們就應該在T[0]…T[k-1]中找到一個合適的位置x，使得T[0]…T[x-1] == T[k-x]…T[k-1]。也就是說，當用T[k]去匹配T[j]失敗時，我們應該用T[x]去匹配T[j]。因此x = next[k]。整個過程相當於用模式串去匹配自身。

[cpp] view plaincopy
  1. #include <iostream>  
  2. #include <cassert>  
  3. using namespace std;  
  4.   
  5. //求next陣列  
  6. //next[j] = k:表示當matchStr[j]失配時，下一次應該用matchStr[k-1]來匹配  
  7. void GetNext( char *str, int *next )  
  8. {     
  9.     if( str == NULL ) return;  
  10.       
  11.     for( int i=0; *(str+i) != '\0'; i++ )  
  12.     {  
  13.         if( i == 0 ) next[i] = 0;     
  14.         else if( i == 1 ) next[i] = 1;  
  15.         else  
  16.         {  
  17.             int tmp = next[i-1];  
  18.             if( str[i-1] == str[tmp-1] ) next[i] = tmp+1;  
  19.             else  
  20.             {                 
  21.                 //如果str[0]...str[j]前後兩端有對稱，找出對稱位置  
  22.                 while( tmp > 1 )  
  23.                 {  
  24.                     if( str[i-1] != str[tmp-1] ) tmp = next[tmp];                     
  25.                     else next[i] = tmp+1;                     
  26.                 }  
  27.                 //如果str[0]...str[j]前後兩端無對稱，則next置1  
  28.                 if( tmp <= 1 ) next[i] = 1;  
  29.             }  
  30.         }  
  31.     }  
  32. }  
  33.   
  34. //字串匹配：KMP演算法，即在mainStr中找到從beginPos開始的第一個匹配位置  
  35. int Kmp( char *mainStr, char *matchStr, int beginPos, int *next )  
  36. {  
  37.     assert( mainStr != NULL && matchStr != NULL && beginPos >= 0 );  
  38.   
  39.     int i, j;  
  40.     for( i=beginPos, j=0; *(mainStr+i) != '\0' && *(matchStr+j) != '\0';  )  
  41.     {  
  42.         //如果mainStr[i] == matchStr[j], 繼續匹配下一個  
  43.         if( *(mainStr+i) == *(matchStr+j) )  
  44.         {     
  45.             i++;  j++;    
  46.         }  
  47.         //如果mainStr[i] ！= matchStr[j]，查詢next陣列，  
  48.         //用matchStr[next[j]-1]與mainStr[i]匹配       
  49.         else    j = next[j]-1;  
  50.     }  
  51.     if( *(matchStr+j) == '\0' ) return i-j;  
  52.     else    return -1;  
  53. }  
  54.   
  55. //字串匹配的一般演算法，要回溯  
  56. int StrMatch( char *mainStr, char *matchStr, int beginPos )  
  57. {     
  58.     int i, j;  
  59.     for( i = beginPos; *(mainStr+i) != '\0'; i++ )  
  60.     {  
  61.         int tmp = i;          
  62.         for( j=0; *(matchStr+j) != '\0'; )  
  63.         {  
  64.             if( *(mainStr+tmp) == *(matchStr+j) )  
  65.             {  
  66.                 tmp++; j++;  
  67.             }  
  68.             else break;  
  69.         }  
  70.         if( *(matchStr+j) == '\0' ) return tmp-j;  
  71.     }  
  72.     return -1;  
  73. }  
  74.   
  75. int main()  
  76. {  
  77.     int next[100];  
  78.     memset( next, 0, sizeof(next) );  
  79.   
  80.     char *mainStr = "ababcabcacbab";  
  81.     char *matchStr = "abcac";  
  82.   
  83.     GetNext( matchStr, next );  
  84.     cout << Kmp( mainStr, matchStr, 0, next ) << endl;  
  85.     cout << StrMatch( mainStr, matchStr, 0 ) << endl;     
  86.     return 0;  
  87. }  

7.取值為[1，n-1] 含n 個元素的整數陣列至少存在一個重複數，O(n) 時間內找出其中任意一個重複數。 

        可以使用類似單連結串列求環的方法解決這個問題。把陣列想想成一個連結串列，這裡用陣列元素的值作為下一個元素在陣列中的索引。

設陣列A共有n個元素，即A={ a0, a1, a2, …, an-1 }。

        首先給出下標n-1，則第一個元素為A[n-1]，然後用A[n-1]-1作為下標，可以到達元素A[A[n-1]-1]，再以A[A[n-1]-1]為下標，可以得到元素A[A[A[n-1]-1]]…可以看到這裡並沒用直接用元素值作索引，而是用元素值減1，這樣做是為了避免陷入死迴圈。

        如果A[i]=A[j]=x，即x在陣列中出現了兩次。則A[i]--->A[x]--->…---> A[j]---> A[x]，因此連結串列邊形成了環。

        一旦連結串列產生後，問題就簡單多了。因為重複出現得到元素恰好是環的入口點。於是，問題就相當於單連結串列求環的入口點。用指標追過的辦法，指標x每次步長為2，指標y每次步長為1。直到x、y相遇，然後重置x，使x重新開始。這次同步移動x、y，每次步長都為1，當x、y再次相遇時，恰好是環的入口點。

[cpp] view plaincopy
  1. //在O(n)的時間內，找出任意重複的一個數  
  2. int FindRepeat( int *data, int size )  
  3. {  
  4.     int x = size;  
  5.     int y = size;  
  6.   
  7.     //找到相遇點  
  8.     do{  
  9.         x = data[data[x-1]-1];  
  10.         y = data[y-1];  
  11.     }while( x != y );  
  12.   
  13.     //找到重複的元素  
  14.     x = size;  
  15.     do{  
  16.         x = data[x-1];  
  17.         y = data[y-1];  
  18.     }while( x != y );  
  19.   
  20.     return x;  
  21. }  
 

相關文章