看雪CTF快訊：

第八題無人破解成功

導語

截至第八題今天中午停止，無人攻破。第八題的作者ccfer以0人攻破的成績成功登上第一位。

攻擊方排名保持不變

現在僅剩只剩下最後一題——九層妖塔，這也是改變排名的最後一次機會！

能否有人絕地反擊？贏得最後的三個名額？

本屆比賽又是否會出現兩個防守方冠軍？讓我們拭目以待！

接下來讓我們一起來看看第八題的設計思路。

看雪評委netwind點評

該題獨具匠心，是根據離散傅立葉變換及逆變換在時域和頻域的關係和性質構造的一個破解題目。題目中內建了一組頻譜Xk和一組離散取樣值xn。用註冊碼後面一部分(C部分)作為頻域梳妝濾波器，從頻率Xk中過濾掉噪聲分量後再做快速傅立葉逆變換(IFFT)得到的時域訊號，與xn去除週期方波干擾（由註冊碼前面一部分A和中間部分B生成）的時域訊號進行匹配，來驗證註冊碼是否有效！

第八題作者簡介

ccfer，從看雪001論壇開始學習脫殼逆向，產生興趣後放棄從事多年的電力系統繼電保護行業，轉行到軟體安全，感謝論壇多年來提供的學習環境，祝看雪論壇越辦越好。

第八題設計思路

系統需求：WIN64

註冊成功提示：Good job!

正確註冊碼：

E36F74E4D69ABAF222B0F684416F121FD5AFC1BE97B0FFE28118AA1C2D2C00DEF63729C8

註冊碼格式：

AAAAAAAAAAAAAAAAAAAAAAAABBBBBBBBBBBBBBBBBBBBBBBBCCCCCCCCCCCCCCCCCCCCCCCC，可分為A，B，C三個部分，轉換成16進位制後，每部分對應12個位元組。

題目概要

利用離散傅立葉變換及逆變換在時域和頻域的關係和性質構造的一個crackme；

維基百科裡解釋：

離散傅立葉變換（Discrete Fourier Transform，縮寫為DFT），是傅立葉變換在時域和頻域上都呈離散的形式，將訊號的時域取樣變換為其DTFT的頻域取樣。在形式上，變換兩端（時域和頻域上）的序列是有限長的，而實際上這兩組序列都應當被認為是離散週期訊號的主值序列。即使對有限長的離散訊號作DFT，也應當將其看作其週期延拓的變換。在實際應用中通常採用快速傅立葉變換計算DFT。

題目中內建了一組頻譜Xk和一組離散取樣值xn，頻譜涵蓋1到96次諧波，取樣點數是256點；

Xk中諧波分量分兩組，一組是訊號量，一組是噪聲量；xn則疊加了週期方波干擾；

用註冊碼C部分作為頻域梳妝濾波器，從頻率Xk中過濾掉噪聲分量後再做快速傅立葉逆變換(IFFT)得到的時域訊號，與xn去除週期方波干擾（由註冊碼A和B部分生成）的時域訊號匹配，那麼註冊碼就是有效的；

驗證關係可以這樣描述：FrequencyDomainFilter(IFFT(Xk), C) = TimeDomainFilter(xn, A, B)；

實際題目中A部分有2個解，B部分有17個解，A和B組合起來共有34組週期方波波形，其中只有一種是能夠匹配成功的，手工窮舉即可完成。

另外為了增加分析難度，題目中的數值儲存都做了簡單的移位交換加密，運算前讀取記憶體中的變數解密，運算後再加密儲存到記憶體變數中。

有關IFFT的運算沒有用系統的浮點數，用的是定點數，把int64解析成高32位的整數部分和低32位的小數部分，本質就是數值的縮放，小數點看不看得見並不重要。

所用的正弦餘弦函式都是事先計算好的，用的時候直接查表了。

演算法描述

下面內容中不加0x字首的均表示10進位制數

1. 第一部分A的演算法是二次剩餘問題，用於干擾時域取樣值的偶數項。

這部分比較簡單，特別的地方在於平方模的實現沒有用到乘法，原理如下：

任意選取一個遠遠大於p的常數F，常數G=F*F*F*F-F+1, 常數H=F*F*F*F+F*F-F+1

g = G % ((A % p) + F) % p

h = H % ((A % p) + F) % p

可以證明出：

g = (A*A*A*A + A + 1) % p

h = (A*A*A*A + A*A + A + 1) % p

於是：

(h – g) % p = A * A % p

不用乘法就求出了A的平方模(想了解這個思路的詳情，可自行前去閱讀h**p://www.matrix67.com/blog/archives/5362)

回到當前題目裡，具體問題是求解下面一個二次剩餘問題：

p = 44876614366229365187800397851

r = 14995684705179149819785261106

A * A % p = r

A用NTL大數庫現成的函式A = SqrRootMod(r, p)可直接求解，或者用RDLP計算器直接算

A = 41150248829223493762924441571，同時（p – A）也是方程的解

因此A部分有2個解：

0x84F6B022F2BA9AD6E4746FE3

0x0C0A609888EB889D7AF28838

2. 第二部分B的演算法是個推廣型的pell方程，用於干擾時域取樣值的奇數項

把B拆開兩半各6位元組長度的x和y。

具體問題是求下面方程的整數解：

5*x*x - 3*y*y = 2

方程解法可用Largrange連分式法或矩陣法，矩陣法的話可以參考下圖中的定理：

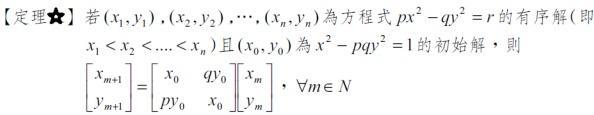
也就是先求出x*x - 3*5*y*y = 1的一個初始解，直接觀察或小範圍窮舉可得初始解:(4，1)

同樣5*x*x - 3*y*y = 2的初始解也很容易得到:(1,1)

再求出變換矩陣：

4    3

5    4

然後方程的所有解都可以依次計算得到了：

//示例演算法，要更多的解__int64會溢位，應該用大數實現，不過就此題而言用__int64也足夠了

int i;

__int64 t;

__int64 x = 1;

__int64 y = 1;

for (i=0;i<20;i++)

{

t = x * 4 + y * 3;

y = x * 5 + y * 4;

x = t;

cout << "x=" << x << endl;

cout << "y=" << y << endl;

}

方程在6位元組的限定的長度範圍內有17組解：

{0x000000000001,0x000000000001}

{0x000000000007,0x000000000009}

{0x000000000037,0x000000000047}

{0x0000000001B1,0x00000000022F}

{0x000000000D51,0x000000001131}

{0x0000000068D7,0x000000008759}

{0x000000033967,0x000000042997}

{0x000000196261,0x00000020C55F}

{0x000000C7D9A1,0x000001020161}

{0x000006256AA7,0x000007EF45A9}

{0x000030637B97,0x00003E782BE7}

{0x00017CF67211,0x0001EBD2198F}

{0x000BB75014F1,0x000F2018A091}

{0x005C3D8A3577,0x007714F2EAF9}

{0x02D6350196C7,0x03A9877EB737}

{0x16556A8280C1,0x1CD52702CEBF}

{0xAFD51F126F41,0xE2FFB097BEC1}

3. 第三部分C的演算法是IFFT，也是本題的核心驗證

內建頻譜Xk經過C值二進位制位遮蔽掉噪聲頻率分量，做IFFT恢復到時域離散訊號，再疊加A和B生成的方波，與內建xn的方差值如果小於一定範圍，則匹配成功。

當前的取樣頻率對於此干擾週期方波來說不能滿足期奈奎斯特取樣的定理的要求（取樣頻率fs.max大於訊號中最高頻率fmax的2倍），所以不必濾除干擾方波直接對xn做FFT得到的結果不會對頻譜分量產生本質變化（當然一定要窮舉A和B組合的34組方波濾除干擾也可以，只是多此一舉，結果一樣），

這樣得到的頻譜和內建的Xk對比，看Xk中缺少了哪些頻率分量，從而確定C中為1的位。

這部分解法程式碼參考單獨附件檔案solvefft.cpp

為了更形象直觀，這部分也可以用matlab來解，示例（輸入的數值都放大了10000倍，方便觀察也省去了小數點，當然這些數值需要有個移位解密過程才能得到）：

N=256;

n=0:N-1;

xn=[513227,352677,120365,184774,16616,165078,350263,17761,-4424,178812,53257,84570,115610,-21613,64830,133790,42358,21409,40276,113004,128339,9542,13155,65564,17442,15923,34815,42483,68112,-24713,-132308,-30929, ...

110352,105703,88405,84805,43179,83137,101041,-22196,-15975,93945,59842,1587,-26834,-37987,4106,-56684,-102642,5277,63189,116651,134388,5713,50300,143057,7244,-3068,68244,-3911,48427,106580,-10550,-23592, ...

41109,-16189,-82771,-43512,12923,-12783,-10204,20307,-58625,-48523,83577,37311,-39703,22208,22715,-1343,26426,-6892,-7910,80561,86954,31208,74282,97360,-17630,-46986,66679,98463,74427,64015,2996,-24930, ...

3154,32702,114887,126063,-18483,-81642,4830,48422,38061,39947,-9388,-62939,-11777,29075,24050,75408,80716,57844,125591,93868,-11953,3692,-8309,-19813,78883,68528,2542,34029,51422,102745,136347,1472,-67837, ...

-14248,-20978,17723,63960,-27387,-39928,65692,75404,52242,63656,24449,-3569,-7254,-61102,-75174,-9543,38489,79760,123357,105866,49227,8961,6916,64732,113072,44956,-55689,-36193,31419,66498,92245,24032, ...

-60894,-8238,-18740,-56942,104151,145732,-21749,-30317,14427,-21412,18577,57060,30899,16957,26605,46860,29167,39755,59726,-3362,66867,157937,25240,54883,156699,-7576,9213,176611,115856,81562,47209,-42200, ...

42500,65973,-7166,30905,30519,37321,54072,-28335,-24790,-26860,-85316,2737,29266,23895,162546,138940,52855,106579,31831,-41245,22391,12292,33032,71533,-17532,-21898,36364,-20140,-58593,-36459,21681,134673, ...

124499,19952,27629,21199,-5272,80325,37049,-56557,64342,42711,-105213,4749,40448,-56697,24845,22456,-50996,29341,29191,-48154,-70042,-38159,6590,-123000,-165431,6374,-56271,-127370,-179473,-467218,-145137];

Xk=[0+0i,0-20000i,122-9999i,981-19975i,368-9993i,490-9987i,1226-19962i,2934-19783i,1715-19926i,3901-19615i,2204-19878i,1224-9924i,5334-19275i,2902-9569i,6273-18990i,6737-18830i, ...

3660-19662i,3826-9238i,2071-9783i,2191-9757i,8992-17864i,9427-17638i,4928-8700i,2667-9637i,10699-16897i,5805-19138i,5758-8175i,11913-16064i,6506-18912i,6737-18830i,6968-18746i,13431-14819i, ...

3713-9285i,14142-14142i,7242-6895i,4052-9142i,15144-13063i,15460-12687i,4386-8986i,16064-11913i,8175-5758i,4713-8819i,16897-10699i,4928-8700i,8700-4928i,17638-9427i,8932-4496i,18079-8551i, ...

5453-8382i,18477-7653i,9329-3598i,9415-3368i,5857-8104i,5956-8032i,9637-2667i,19400-4859i,12497-15614i,12687-15460i,6438-7651i,9891-1467i,6624-7491i,13431-14819i,9972-735i,19975-981i, ...

6983-7157i,9999+0i,9996+245i,9987+490i,7326-6806i,7409-6715i,9924+1224i,15144-13063i,19705+3419i,9807+1950i,7807-6248i,19400+4859i,7958-6055i,8032-5956i,16209-11715i,18830+6737i, ...

18659+7197i,18477+7653i,9142+4052i,18079+8551i,17864+8992i,8819+4713i,17401+9857i,8577+5141i,8760-4821i,17638-9427i,17752-9210i,8032+5956i,8986-4386i,9039-4275i,9091-4164i,14819+13431i, ...

14484+13790i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...

0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...

0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...

0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...

14484-13790i,14819-13431i,9091+4164i,9039+4275i,8986+4386i,8032-5956i,17752+9210i,17638+9427i,8760+4821i,8577-5141i,17401-9857i,8819-4713i,17864-8992i,18079-8551i,9142-4052i,18477-7653i, ...

18659-7197i,18830-6737i,16209+11715i,8032+5956i,7958+6055i,19400-4859i,7807+6248i,9807-1950i,19705-3419i,15144+13063i,9924-1224i,7409+6715i,7326+6806i,9987-490i,9996-245i,10000+0i, ...

6983+7157i,19975+981i,9972+735i,13431+14819i,6624+7491i,9891+1467i,6438+7651i,12687+15460i,12497+15614i,19400+4859i,9637+2667i,5956+8032i,5857+8104i,9415+3368i,9329+3598i,18477+7653i, ...

5453+8382i,18079+8551i,8932+4496i,17638+9427i,8700+4928i,4928+8700i,16897+10699i,4713+8819i,8175+5758i,16064+11913i,4386+8986i,15460+12687i,15144+13063i,4052+9142i,7242+6895i,14142+14142i, ...

3713+9285i,13431+14819i,6968+18746i,6737+18830i,6506+18912i,11913+16064i,5758+8175i,5805+19138i,10699+16897i,2667+9637i,4928+8700i,9427+17638i,8992+17864i,2191+9757i,2071+9783i,3826+9238i, ...

3660+19662i,6737+18830i,6273+18990i,2902+9569i,5334+19275i,1224+9924i,2204+19878i,3901+19615i,1715+19926i,2934+19783i,1226+19962i,490+9987i,368+9993i,981+19975i,122+9999i,0+20000i];

plot(n(1:255),xn(1:255)/10000);

先看看xn的時域波形，沒啥用，就是想看看它長啥樣：

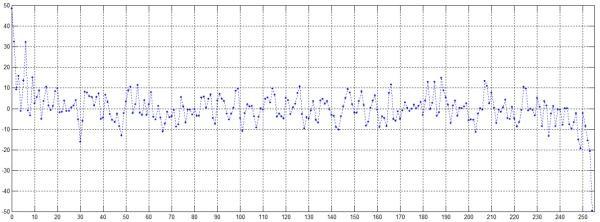
Xk1=fft(xn)/N*2;

plot(n(1:96),abs(Xk1(1:96)/10000),n(1:96),abs(Xk(1:96))/10000);

然後畫出對比頻譜圖（直接畫出的是帶線條的，我們只關心離散的點，所以修改一下顯示設定：兩條線的LineStyle選none，Marker一條選綠色o，另一條選紅色x）：

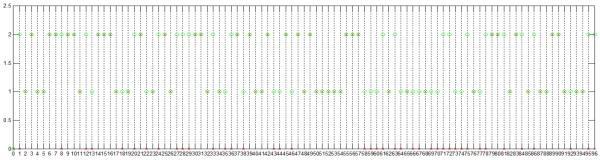
圖中綠o內建的頻譜分量幅值，紅x是直接對內建xn經FFT後得到的頻譜分量幅值，可以看出綠o涵蓋了1到96次諧波所有的頻率分量，而紅x是有一部分頻率分量的幅值是0的，表示不含有此頻率諧波。

根據落在橫座標軸上（排除0是直流分量）從96到1的紅x由高位到低位構成的大數就能得到註冊碼的C部分0xC82937F6DE002C2D1CAA1881

驗證結果：把ABC各種組合拼起來(注意所用的大數小端在前，位元組序列要翻轉)就得到了34個的待定的註冊碼：

E36F74E4D69ABAF222B0F6840100000000000100000000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F6840700000000000900000000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F6843700000000004700000000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684B101000000002F02000000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684510D000000003111000000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684D768000000005987000000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F6846739030000009729040000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F6846162190000005FC5200000008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684A1D9C70000006101020100008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684A76A25060000A945EF0700008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684977B63300000E72B783E00008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F6841172F67C01008F19D2EB01008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684F11450B70B0091A018200F008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F68477358A3D5C00F9EAF21477008118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684C7960135D60237B77E87A9038118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684C180826A5516BFCE0227D51C8118AA1C2D2C00DEF63729C8

E36F74E4D69ABAF222B0F684416F121FD5AFC1BE97B0FFE28118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C0100000000000100000000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C0700000000000900000000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C3700000000004700000000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CB101000000002F02000000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C510D000000003111000000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CD768000000005987000000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C6739030000009729040000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C6162190000005FC5200000008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CA1D9C70000006101020100008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CA76A25060000A945EF0700008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C977B63300000E72B783E00008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C1172F67C01008F19D2EB01008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CF11450B70B0091A018200F008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C77358A3D5C00F9EAF21477008118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CC7960135D60237B77E87A9038118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0CC180826A5516BFCE0227D51C8118AA1C2D2C00DEF63729C8

3888F27A9D88EB8898600A0C416F121FD5AFC1BE97B0FFE28118AA1C2D2C00DEF63729C8

最後能檢驗透過的是中間那個綠色的。

溫馨提示

每道題結束過後都會看到很多盆友的精彩解題分析過程，因為公眾號內容的限制，每次題目過後我們將選出一篇與大家分享。解題方式多種多樣，各位參賽選手的腦洞也種類繁多，想要看到更多解題分析的小夥伴們可以前往看雪論壇【CrackMe】版塊檢視哦！