看雪.WiFi萬能鑰匙 CTF 2017第十三題 點評及解題思路

Editor發表於2017-06-28
WiFi


看雪CTF 2017 比賽進行至第十三題

截止至今天中午12點，第十三題破解人數為 2 人！

防守方 hsadkhk 依然位居首位~

看雪.WiFi萬能鑰匙 CTF 2017第十三題 點評及解題思路

此題過後，風間仁依然處於第一位~，kkHAIKE升至第二位。

看雪.WiFi萬能鑰匙 CTF 2017第十三題 點評及解題思路

比賽進入尾聲，僅剩 2 題。

對於比賽前幾名的爭奪戰，將在前十名之間展開。

期待ing......

接下來我們來回顧一下第十三題

看看 看雪評委和出題者是怎麼說的ヾ(๑╹◡╹)ﾉ"。


看雪評委 netwind 點評


此題考查攻方選手對演算法的分析能力。該題演算法模型是：考慮一條有限域橢圓曲線上的已知點 G1, G2, 以及給定的係數 h1,h2,h3,求點S(x,y) 滿足方程：h1( S + h3*G1) = h2(S + h3*G2)  mod n，判斷正確的key等價於判斷方程兩邊運算的點的x座標： 兩個大數相等。如果對演算法模型不熟悉，做起來可能會有一定難度。


作者簡介


論壇ID為readyu，畢業於中國科學技術大學自動控制專業，從事軟體開發多年。在軟體保護技術、加密演算法方面有一些體會。曾在北京多看科技從事電子閱讀加密技術的研究，現在MIUI做系統與安全相關的工作。


看雪 CTF 2017 第十二題設計思路


根據規則，crackme 內部name固定。 SN唯一。
本題sn為：
7A7102F36F3B344D666132A6FF7EF4BA05B99640BB815C9E712A72C64B6ABC582C2

正確提示：
"Oh Yes! You got it.",


設計思路：

（1）考慮一條有限域橢圓曲線上的已知點 G1, G2, 以及給定的係數 h1,h2,h3,求點S(x,y) 滿足方程, 以下大寫字母表示有限域橢圓曲線上的點， 小寫字母表示數值：

h1( S + h3*G1) = h2(S + h3*G2)   mod n

那麼， 判斷正確的key， 等價於判斷方程兩邊運算的點的x座標： 兩個大數相等。

因此， 比較key，不會出現明文比較。這裡S是可以計算的，並沒有用到ECDLP（橢圓曲線離散對數）。

那麼，如何求出S(x,y)：

=> (h1 - h2) S = h2*h3*G2 - h1*h3*G1

S(x,y) = (h2*h3/(h1 - h2)) * G2-  (h1*h3/(h1 - h2)) * G1  mod n

sn = S(x,y) ， x,y is the point on the cuver ECC2K-130

橢圓曲線選取公開的ECC2K-130：

（引數取自如下pdf文件）

http://www.ecc-challenge.info/anon.pdf

========
ECC2K-130   GF(2^m)
========
E:     y^2  + xy =   x^3 + a*x^2 + b  

m = 131
f = x^131 + x^13 + x^2 + x + 1

a = 0
b = 1

E 即：  y^2 + xy = x^3 + 1  , over  GF(2^131)

point P (G1)：
X= 51C99BFA6F18DE467C80C23B98C7994AA
Y= 42EA2D112ECEC71FCF7E000D7EFC978BD

Point Q (G2)：
X= 6C997F3E7F2C66A4A5D2FDA13756A37B1
Y= 4A38D11829D32D347BD0C0F584D546E9A

np (number of points) = 80000000000000001353F755C0E8FC9A4

n  (prime order) = 200000000000000004D4FDD5703A3F269

（2） 補充細節的考慮 之一 關於hash。

為了使得h1, h2, h3 線性無關，並且與name, 和相關字元 關聯起來， 這裡取md5 hash作為係數。
h1 = hash1(0x1 name - pediy);
h2 = hash2(0x2 0x2 name - 2017);
h3 = hash3(0x3 0x3 0x3 name - crackme);
hash 採用md5

例如： name = readyu

readyu-pediy
hexstring= 017265616479752D7065646979
hash1=
51c75f1f444baa97ed18dd6c340835d7

readyu-2017
hexstring= 02027265616479752D32303137
hash2=
0e5cf7f068d6efa16f42f935ec424a75

readyu-crackme
hexstring= 0303037265616479752D637261636B6D65
hash3=
a4cd1d64486abde1be441944460cd41d

（3） 

補充細節的考慮 之二 關於sn 編碼。

採用一個素數P269， 把S（x,y） 用d加密編碼。 結果就是sn。用到了費馬小定理。
sn = S^d mod P

P269(prime)= 10000000000000000000000000000000000000000000000000000000000000000079

e=0x5

d= CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCD2D

這裡有：
m^(P-1) = 1 (mod P)    (m為自然數， P為素數，  1 <= m < P) 費馬小定理
e*d = 1   （ mod  (P-1) ）   , 素數P的尤拉函式是P-1

=〉
(m^d)^e  = m  ( mod P)


（4） 答案：

計算hash：
readyu-pediy
017265616479752D7065646979
hash1 = 51c75f1f444baa97ed18dd6c340835d7

readyu-2017
02027265616479752D32303137
hash2 = 0e5cf7f068d6efa16f42f935ec424a75

readyu-crackme
0303037265616479752D637261636B6D65
hash3 = a4cd1d64486abde1be441944460cd41d

計算S(x,y)：
h1=51C75F1F444BAA97ED18DD6C340835D7
h2=0E5CF7F068D6EFA16F42F935EC424A75
h3=A4CD1D64486ABDE1BE441944460CD41D
G1(x,y)=(51C99BFA6F18DE467C80C23B98C7994AA , 42EA2D112ECEC71FCF7E000D7EFC978BD)
G2(x,y)=(6C997F3E7F2C66A4A5D2FDA13756A37B1 , 4A38D11829D32D347BD0C0F584D546E9A)

S(x,y) = (h2*h3/(h1 - h2)) * G2 - (h1*h3/(h1 - h2)) * G1  mod Order

Order = 200000000000000004D4FDD5703A3F269

h1 - h2 = 436A672EDB74BAF67DD5E43


下面選取攻擊者 風間仁 的破解分析


1. 處理邏輯

name是內建的: readyu

code是輸入的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int __cdecl sub_40AEF0(HWND hDlg)
{
    ...
  GetDlgItemTextA(hDlg, 1000, name, 64);
  v1 = GetDlgItemTextA(hDlg, 1001, code, 256);
  v2 = v1;
  if ( v1 >= 0x21 )
  {
    if ( code[0] != 0x30 )
    {
      v3 = 0;
      if ( v1 <= 0 )
      {
LABEL_9:
        memset(byte_41BC84, 0, sizeof(byte_41BC84));
        v5 = off_418078[check(code, name)];
        MessageBoxA(hDlg, v5, v5, 0);
        return 0;
      }
      while ( 1 )
      {
        v4 = code[v3];
        if ( !isxdigit(v4) || islower(v4) )
          break;
        if ( ++v3 >= v2 )
          goto LABEL_9;
      }
    }
    ...
}


z = 10000000000000000000000000000000000000000000000000000000000000000079

r = code ^ 5 mod z

r有34位元組,  前17位元組作為x,  後17位元組作為y

epInput = (x,y)


根據name計算3個md5值:

md0=md5("\x01readyu-pediy")=51C75F1F444BAA97ED18DD6C340835D7

md1=md5("\x02\x02readyu-2017")=0E5CF7F068D6EFA16F42F935EC424A75

md2=md5("\x03\x03\x03readyu-crackme")=A4CD1D64486ABDE1BE441944460CD41D


橢圓曲線: m=131, a=13, b=2, c=1, a2=0, a6=1

前面的epInput是這個曲線上的點

ep1 = ( 51C99BFA6F18DE467C80C23B98C7994AA, 42EA2D112ECEC71FCF7E000D7EFC978BD )

ep2 = ( 6C997F3E7F2C66A4A5D2FDA13756A37B1, 4A38D11829D32D347BD0C0F584D546E9A )

n = 200000000000000004D4FDD5703A3F269

校驗 (md2 * ep1 + epInput) * md0 mod n == (md2 *ep2 + epInput) * md1 mod n


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
signed int __cdecl check(char *code, const char *a2)
{
    ...
  get_mip();
  v29[0] = 0;
  memset(&v29[1], 0, 0x20u);
  *(_WORD *)&v29[33] = 0;
  v29[35] = 0;
  ptr[0] = 0x10;
  ptr[1] = 0;
  ptr[2] = 0;
  ptr[3] = 0;
  ptr[4] = 0;
  ptr[5] = 0;
  ptr[6] = 0;
  ptr[7] = 0;
  ptr[8] = 0;
  ptr[9] = 0;
  ptr[10] = 0;
  ptr[11] = 0;
  ptr[12] = 0;
  ptr[13] = 0;
  ptr[14] = 0;
  ptr[15] = 0;
  ptr[16] = 0;
  ptr[17] = 0;
  ptr[18] = 0;
  ptr[19] = 0;
  ptr[20] = 0;
  ptr[21] = 0;
  ptr[22] = 0;
  ptr[23] = 0;
  ptr[24] = 0;
  ptr[25] = 0;
  ptr[26] = 0;
  ptr[27] = 0;
  ptr[28] = 0;
  ptr[29] = 0;
  ptr[30] = 0;
  ptr[31] = 0;
  ptr[32] = 0;
  ptr[33] = 0x79;
  mirsys_init();
  v2 = z;
  a2_1 = ::a2;
  v4 = ::x;
  y = dword_41BC68;
  x = dword_41BC64;
  a6 = dword_41BC70;
  w = dword_41BC74;
  bytes_to_big(34, ptr, z);
  cinstr(v4, code);
  if ( mr_compare(v4, v2) <= 0 )
  {
    power(v4, 5, v2, w);
    memset(v29, 0, sizeof(v29));
    if ( big_to_bytes(34, w, v29, 1) == 34 )
    {
      bytes_to_big(17, v29, x);
      bytes_to_big(17, &v29[17], y);
      convert(0, a2_1);
      convert(1, a6);
      v17 = 1;
      if ( ecurve2_init(131, 13, 2, 1, a2_1, a6, 0, 0) )
      {
        qmemcpy(v46, "51C99BFA6F18DE467C80C23B98C7994AA", sizeof(v46));
        qmemcpy(v47, "42EA2D112ECEC71FCF7E000D7EFC978BD", sizeof(v47));
        qmemcpy(v44, "6C997F3E7F2C66A4A5D2FDA13756A37B1", sizeof(v44));
        qmemcpy(v43, "4A38D11829D32D347BD0C0F584D546E9A", sizeof(v43));
        qmemcpy(v45, "200000000000000004D4FDD5703A3F269", sizeof(v45));
        v30 = dword_418118;
        v31 = word_41811C;
        memset(v32, 0, sizeof(v32));
        v33 = 0;
        v34 = dword_4180E4;
        v35 = byte_4180E8;
        memset(v36, 0, sizeof(v36));
        v37 = 0;
        v38 = 0;
        v40 = dword_4180F0;
        v39 = dword_4180EC;
        memset(v41, 0, sizeof(v41));
        a1 = 0;
        memset(v49, 0, sizeof(v49));
        v50 = 0;
        v51 = 0;
        i = 0;
        v6 = &a1;
        a3 = (char *)mds;
        lpMem = (flash)&v30;
        do
        {
          strcpy(v6, a2);
          strcat(v6, "-");
          strcat(v6, (const char *)lpMem);
          xmd5(v6, strlen(v6), a3, i + 1);
          v6 += 256;
          ++i;
          lpMem += 4;
          a3 += 16;
        }
        while ( i < 3 );
        md0 = mirvar(0);
        md1 = mirvar(0);
        md2 = mirvar(0);
        x1 = mirvar(0);
        a3a = mirvar(0);
        x2 = mirvar(0);
        lpMema = mirvar(0);
        v9 = mirvar(0);
        ep1 = epoint_init();
        ep2 = epoint_init();
        p1 = epoint_init();
        p2 = epoint_init();
        epInput = epoint_init();
        if ( epoint2_set(x, y, 0, epInput) )
        {
          cinstr(x1, v46);
          cinstr(a3a, v47);
          epoint2_set(x1, a3a, 0, ep1);
          cinstr(x2, v44);
          cinstr(lpMema, v43);
          epoint2_set(x2, lpMema, 0, ep2);
          bytes_to_big(16, (_BYTE *)mds, md0);
          bytes_to_big(16, mds[1], md1);
          bytes_to_big(16, mds[2], md2);
          ecurve2_mult(md2, ep1, p1);
          ecurve2_mult(md2, ep2, p2);
          ecurve2_add(epInput, p1);
          ecurve2_add(epInput, p2);
          ecurve2_mult(md0, p1, p1);
          ecurve2_mult(md1, p2, p2);
          epoint2_get(p1, x1, a3a);
          epoint2_get(p2, x2, lpMema);
          cinstr(v9, v45);
          divide(x1, v9, v9);
          divide(x2, v9, v9);
          v17 = 3;
          if ( !mr_compare(x1, x2) )
            v17 = 0;
        }
        else
        {
          v17 = 2;
        }
        mirkill(md0);
        mirkill(md1);
        mirkill(md2);
        mirkill(x1);
        mirkill(x2);
        mirkill(a3a);
        mirkill(lpMema);
        mirkill(v9);
        epoint_free(ep1);
        epoint_free(ep2);
        epoint_free(p1);
        epoint_free(p2);
        epoint_free(epInput);
      }
      mirexit();
      result = v17;
    }
    else
    {
      mirexit();
      result = 1;
    }
  }
  else
  {
    mirexit();
    result = 1;
  }
  return result;
}


2. 計算


(md2 * ep1 + epInput) * md0 mod n == (md2 *ep2 + epInput) * md1 mod n

=>

epInput = (md2 * md1 * ep2 - md2 * md0 * ep1) * (((md0 - md1) ^-1) mod n)

得到 ( 02D23461BA71B50AF182DC76E5A7C726F5, 07BE013AF19BD185BCD20BB341EA31298B )

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
void test2()
{
    big a2 = mirvar(0);
    big a6 = mirvar(1);
    if (ecurve2_init(131, 13, 2, 1, a2, a6, 0, 0))
    {
        epoint *epInput = epoint_init();
        big x = mirvar(0);
        big y = mirvar(0);
         
        big md0 = mirvar(0);
        big md1 = mirvar(0);
        big md2 = mirvar(0);
        cinstr(md0, "51C75F1F444BAA97ED18DD6C340835D7");
        cinstr(md1, "0E5CF7F068D6EFA16F42F935EC424A75");
        cinstr(md2, "A4CD1D64486ABDE1BE441944460CD41D");
         
        epoint *p1 = epoint_init();
        big x1 = mirvar(0);
        big y1 = mirvar(0);
        cinstr(x1, "51C99BFA6F18DE467C80C23B98C7994AA");
        cinstr(y1, "42EA2D112ECEC71FCF7E000D7EFC978BD");
        epoint2_set(x1, y1, 0, p1);
         
        epoint *p2 = epoint_init();
        big x2 = mirvar(0);
        big y2 = mirvar(0);
        cinstr(x2, "6C997F3E7F2C66A4A5D2FDA13756A37B1");
        cinstr(y2, "4A38D11829D32D347BD0C0F584D546E9A");
        epoint2_set(x2, y2, 0, p2);
         
        big n = mirvar(0);
        cinstr(n, "200000000000000004D4FDD5703A3F269");
         
        ecurve2_mult(md2, p2, p2);
        ecurve2_mult(md1, p2, p2);
        ecurve2_mult(md2, p1, p1);
        ecurve2_mult(md0, p1, p1);
        ecurve2_sub(p1, p2);
         
        big r = mirvar(0);
        big rd = mirvar(0);
        big nd = mirvar(0);
        big z = mirvar(0);
        subtract(md0, md1, r);
        xgcd(r, n, rd, nd, z);
         
        ecurve2_mult(rd, p2, epInput);
     
        epoint2_get(epInput, x, y);
        char sx[256];
        char sy[256];
        cotstr(x, sx);
        cotstr(y, sy);
        printf("%s\n", sx);
        printf("%s\n", sy);
    }
}


用RDLP計算得到code

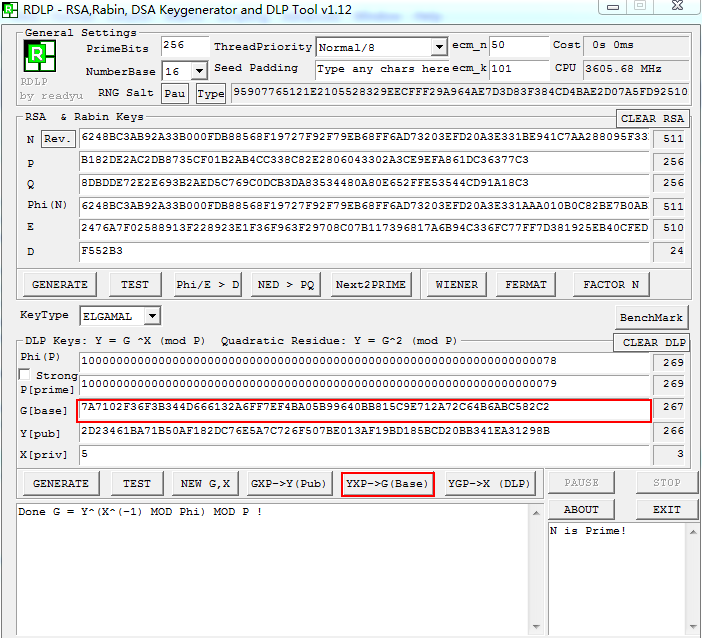
看雪.WiFi萬能鑰匙 CTF 2017第十三題 點評及解題思路

>>> 7A7102F36F3B344D666132A6FF7EF4BA05B99640BB815C9E712A72C64B6ABC582C2


相關文章