這個系列的前三篇,介紹了Hacker News,Reddit和Stack Overflow的排名演算法。
今天,討論一個更一般的數學模型。
這個系列的每篇文章,都是可以分開讀的。但是,為了保證所有人都在同一頁上,我再說一下,到目前為止,我們用不同方法,企圖解決的都是同一個問題:根據使用者的投票,決定最近一段時間內的"熱文排名"。
你可能會覺得,這是一個全新的課題,伴隨著網際網路而產生,需要全新的方法來解決。但是,實際上不是。我們可以把"熱文排名"想象成一個"自然冷卻"的過程:
(1)任一時刻,網站中所有的文章,都有一個"當前溫度",溫度最高的文章就排在第一位。
(2)如果一個使用者對某篇文章投了贊成票,該文章的溫度就上升一度。
(3)隨著時間流逝,所有文章的溫度都逐漸"冷卻"。
這樣假設的意義,在於我們可以照搬物理學的冷卻定律,使用現成的公式,建立"溫度"與"時間"之間的函式關係,輕鬆構建一個"指數式衰減"(Exponential decay)的過程。
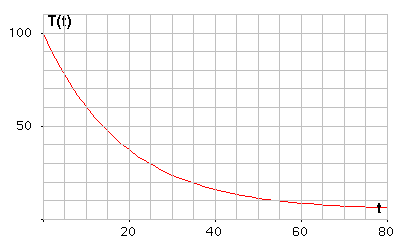
偉大的物理學家牛頓,早在17世紀就提出了溫度冷卻的數學公式,被後人稱作"牛頓冷卻定律"(Newton's Law of Cooling)。我們就用這個定律構建排名演算法。

"牛頓冷卻定律"非常簡單,用一句話就可以概況:
物體的冷卻速度,與其當前溫度與室溫之間的溫差成正比。
寫成數學公式就是:
其中,
- T(t)是溫度(T)的時間(t)函式。微積分知識告訴我們,溫度變化(冷卻)的速率就是溫度函式的導數T'(t)。
- H代表室溫,T(t)-H就是當前溫度與室溫之間的溫差。由於當前溫度高於室溫,所以這是一個正值。
- 常數α(α>0)表示室溫與降溫速率之間的比例關係。前面的負號表示降溫。不同的物質有不同的α值。
這是一個微分方程,為了計算當前溫度,需要求出T(t)的函式表示式。
第一步,改寫方程,然後等式兩邊取積分。
第二步,求出這個積分的解(c為常數項)。
第三步,假定在時刻t0,該物體的溫度是T(t0),簡寫為T0。代入上面的方程,得到
第四步,將上一步的C代入第二步的方程。
假定室溫H為0度,即所有物體最終都會"冷寂",方程就可以簡化為
上面這個方程,就是我們想要的最終結果:
本期溫度 = 上一期溫度 x exp(-(冷卻係數) x 間隔的小時數)
將這個公式用在"排名演算法",就相當於(假定本期沒有增加淨贊成票)
本期得分 = 上一期得分 x exp(-(冷卻係數) x 間隔的小時數)
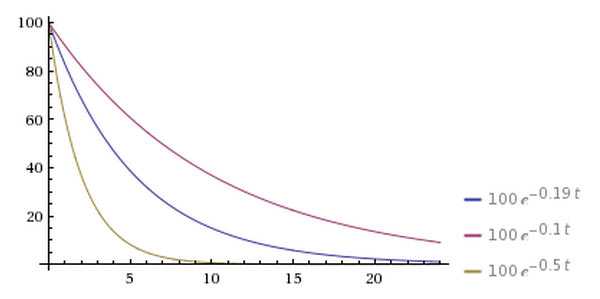
其中,"冷卻係數"是一個你自己決定的值。如果假定一篇新文章的初始分數是100分,24小時之後"冷卻"為1分,那麼可以計算得到"冷卻係數"約等於0.192。如果你想放慢"熱文排名"的更新率,"冷卻係數"就取一個較小的值,否則就取一個較大的值。
[參考文獻]
* Rank Hotness With Newton's Law of Cooling
(完)