在過去幾週中，我們開始對機器學習有了更多的瞭解，也認識到機器學習在機器視覺、影像分類和深度學習領域的重要作用。
我們已經看到卷積神經網路，如LetNet，可以用於對MNIST資料集的手寫字跡進行分類。我們使用了k-NN演算法來識別一張圖片中是否含有貓或狗，並且我們也已經學習瞭如何調參來優化模型，進而提高分類精度。
然而，還有一個重要的機器學習的演算法我們尚未涉及：這個演算法非常容易構建，並能很自然地擴充套件到神經網路和卷積神經網路中。
是什麼演算法呢？
它是一個簡單的線性分類器，並且由於其演算法很直觀，被認為是更多高階的機器學習和深度學習演算法的基石。
繼續閱讀來加深你對線性分類器的認識，以及如何使用它們進行影像分類。
Python線性分類模型簡介
本教程的前半部分主要關注線性分類有關的基本原理和數學知識。總的來說，線性分類指的是那些真正從訓練資料中“學習”的有參分類演算法。
在這裡，我提供了一個真正的線性分類實現程式碼，以及一個用scikit-learn對一張圖片中的內容分類的例子。
4大引數化學習和線性分類的元件
我已經多次使用“引數化”,但它到底是什麼意思？
簡而言之：引數化是確定模型必要引數的過程。
在機器學習的任務中，引數化根據以下幾個方面來確定面對的問題：
- 資料：這是我們將要學習的輸入資料。這些資料包括了資料點（例如，特徵向量，顏色矩陣，原始畫素特徵等）和它們對應的標籤。
- 評分函式：一個函式接收輸入資料，然後將資料匹配到類標籤上。例如，我們輸入特徵向量後，評分函式就開始處理這些資料，呼叫某個函式f（比如我們的評分函式），最後返回預測的分類標籤。
- 損失函式：損失函式可以量化預測的類標籤與真實的類標籤之間的匹配程度。這兩個標籤集合之間的相似度越高，損失就越小（即分類精度越高）。我們的目標是最小化損失函式，相應就能提高分類精度。
- 權重矩陣：權重矩陣，通常標記為W，它是分類器實際優化的權重或引數。我們根據評分函式的輸出以及損失函式，調整並優化權重矩陣，提高分類精度。
注意：取決於你使用的模型的種類，引數可能會多的多。但是在最底層，你會經常遇到4個引數化學習的基本模組。
一旦確定了這4個關鍵元件，我們就可以使用優化方法來找到評分函式的一組引數W，使得損失函式達到最小值（同時提升對資料的分類準確度）
接下來，我們就將看到如何利用這些元件，搭建一個將輸入資料轉化為真實預測值的分類器。
線性分類器：從圖片到標籤
在這部分中，我們將更多的從數學角度研究引數模型到機器學習。
首先，我們需要資料。假設訓練資料集（圖片或者壓縮後的特徵向量）標記為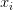
，每個圖或特徵向量都有對應的類標籤 
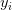。我們用 
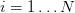和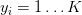
表示有N個D維（特徵向量的長度）的資料點，劃分到K個唯一的類別中。
為了這些表示式更具體點，參考我們以前的教程：基於提取後的顏色矩陣，使用knn分類器識別圖片中的貓和狗。
這份資料集中，總共有N=25，000張圖片，每張圖片的特徵都是一個3D顏色直方圖，其中每個管道有8個桶。這樣產出的特徵向量有D=8 x 8 x 8 = 512個元素。最後，我們有k=2個類別標籤，一個是“狗”，另一個是“貓”。
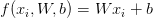
有了這些變數後，我們必須定義一個評分函式f，將特徵向量對映到類標籤的打分上。正如本篇部落格標題所說，我們將使用一個簡單的線性對映：
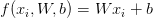
我們假設每個 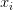都由一個形狀為[D x 1]的單列向量所表示。我們在本例中要再次使用顏色直方圖，不過如果我們使用的是原始畫素粒度，那可以直接把圖片中的畫素壓扁到一個單列向量中。
我們的權重矩陣W形狀為[K x D]（類別標籤數乘以特徵向量的維數）
最後，偏置矩陣b,大小為[K x 1]。實質上，偏置矩陣可以讓我們的評分函式向著一個或另一個方向“提升”，而不會真正影響權重矩陣W，這點往往對學習的成功與否非常關鍵。
回到Kaggle的貓和狗例子中， 每個都表示為512維顏色直方圖，因此的形狀是[512 x 1]。權重矩陣W的形狀為[2 x 512]，而偏置矩陣b為[2 x 1]。
下面展示的是線性分類的評分函式f
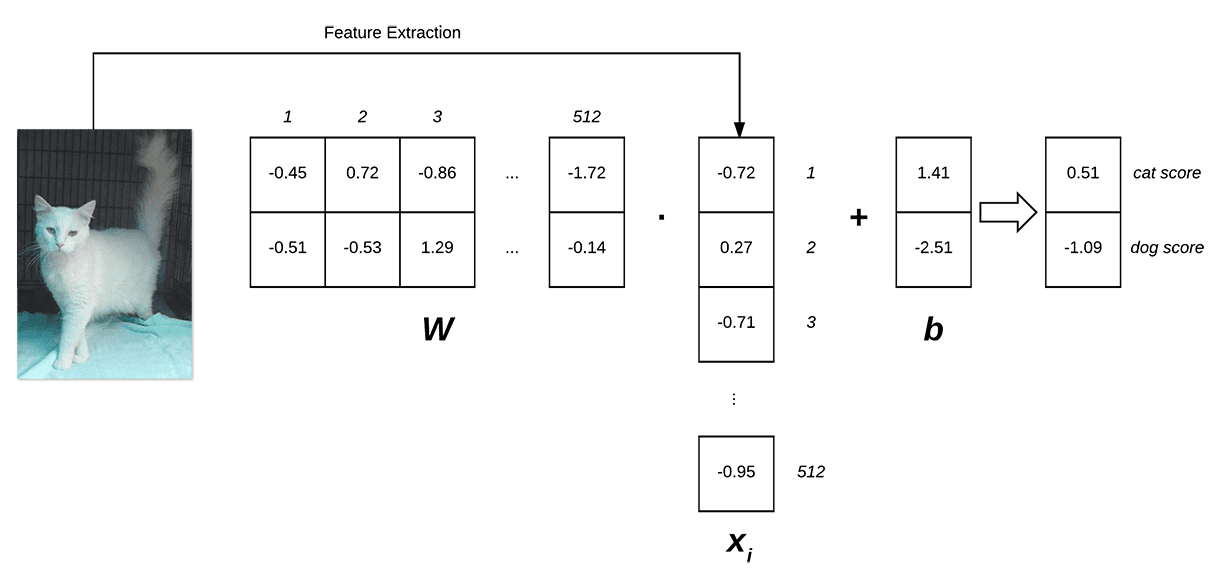
在上圖的左側是原始輸入圖片，我們將從中提取特徵。在本例中，我們計算的是一個512維的顏色直方圖，也可以用其他一些特徵表示方式（包括原始畫素密度），但是對於這個例子，我們就只用顏色分佈，即直方圖來表示xi。
然後我們有了權重矩陣W，有2行（每個類標籤一行）和512列（每一列都是特徵向量中的條目）
將W和xi點乘後，再加上大小為[2 x 1]的偏置矩陣bi。
最後就得到了右邊的兩個值：貓和狗標籤各自的分數。
看著上面的公式，你可以確信輸入xi和yi都是固定的，沒法修改。我們當然可以通過不同的特徵提取技術來得到不同的xi，但是一旦特徵抽取後，這些值就不會再改變了。
實際上，我們唯一能控制的引數就是權重矩陣W以及偏置向量b。因此，我們的目標是利用評分函式和損失函式去優化權重和偏置向量，來提升分類的準確度。
如何優化權重矩陣則取決於我們的損失函式，但通常會涉及梯度下降的某種形式。我們會在以後的部落格中重溫優化和損失函式的概念，不過現在只要簡單理解為給定了一個評分函式後，我們還需要定義一個損失函式，來告訴我們對於輸入資料的預測有多“好”。
引數學習和線性分類的優點
利用引數學習有兩個主要的優點，正如我上面詳述的方法：
- 一旦我們訓練完了模型，就可以丟掉輸入資料而只保留權重矩陣W和偏置向量b。這大大減少了模型的大小，因為我們只需要儲存兩個向量集合（而非整個訓練集）。
- 對新的測試資料分類很快。為了執行分類，我們要做的只是點乘W和xi，然後再加上偏置b。這樣做遠比將每個測試點和整個訓練集比較（比如像knn演算法那樣）快的多。
既然我們理解了線性分類的原理，就一起看下如何在python，opencv和scikit-learn中實現。
使用python，opencv和scikit-learn對圖片線性分類
就像在之前的例子Kaggle 貓vs狗資料集和knn演算法中，我們將從資料集中提取顏色直方圖，不過和前面例子不同的是，我們將用一個線性分類器，而非knn。
準確地說，我們將使用線性支援向量機（SVM），即在n維空間中的資料之間構造一個最大間隔分離超平面。這個分離超平面的目標是將類別為i的所有（或者在給定的容忍度下，儘可能多）的樣本分到超平面的一邊，而所有類別非i的樣本分到另一邊。
關於支援向量機的具體描述已經超出本部落格的範圍。（不過在PyImageSearch Gurus course有詳細描述）
同時，只需知道我們的線性SVM使用了和本部落格“線性分類器：從圖片到標籤”部分中相似的評分函式，然後使用損失函式，用於確定最大分離超平面來對資料點分類（同樣，我們將在以後的部落格中講述損失函式）。
我們從開啟一個新檔案開始，命名為linear_classifier.py，然後插入以下程式碼：
|
1 2 3 4 5 6 7 8 9 10 11 |
# import the necessary packages from sklearn.preprocessing import LabelEncoder from sklearn.svm import LinearSVC from sklearn.metrics import classification_report from sklearn.cross_validation import train_test_split from imutils import paths import numpy as np import argparse import imutils import cv2 import os |
從第2行至11行匯入了必須的python包。我們要使用scikit-learn庫，因此如果你還沒安裝的話，跟著這些步驟，確保將其安裝到你機器上。
我們還將使用我的imutils包，用於方便處理影像的一系列函式。如果你還沒有安裝imutils，那就讓pip安裝。
|
1 |
$ pip install imutils |
現在我們定義extract_color_histogram 函式，用於提取和量化輸入圖片的內容：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def extract_color_histogram(image, bins=(8, 8, 8)): # extract a 3D color histogram from the HSV color space using # the supplied number of `bins` per channel hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV) hist = cv2.calcHist([hsv], [0, 1, 2], None, bins, [0, 180, 0, 256, 0, 256]) # handle normalizing the histogram if we are using OpenCV 2.4.X if imutils.is_cv2(): hist = cv2.normalize(hist) # otherwise, perform "in place" normalization in OpenCV 3 (I # personally hate the way this is done else: cv2.normalize(hist, hist) # return the flattened histogram as the feature vector return hist.flatten() |
這個函式接收一個輸入image ，將其轉化為HSV顏色空間，然後利用為每個通道提供的bins，計算3D顏色直方圖。
利用cv2.calcHist函式計算出顏色直方圖後，將其歸一化後返回給呼叫函式。
有關extract_color_histogram方法更詳細的描述，參閱這篇部落格。
接著，我們從命令列解析引數，並初始化幾個變數:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# import the necessary packages from sklearn.preprocessing import LabelEncoder from sklearn.svm import LinearSVC from sklearn.metrics import classification_report from sklearn.cross_validation import train_test_split from imutils import paths import numpy as np import argparse import imutils import cv2 import os def extract_color_histogram(image, bins=(8, 8, 8)): # extract a 3D color histogram from the HSV color space using # the supplied number of `bins` per channel hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV) hist = cv2.calcHist([hsv], [0, 1, 2], None, bins, [0, 180, 0, 256, 0, 256]) # handle normalizing the histogram if we are using OpenCV 2.4.X if imutils.is_cv2(): hist = cv2.normalize(hist) # otherwise, perform "in place" normalization in OpenCV 3 (I # personally hate the way this is done else: cv2.normalize(hist, hist) # return the flattened histogram as the feature vector return hist.flatten() # construct the argument parse and parse the arguments ap = argparse.ArgumentParser() ap.add_argument("-d", "--dataset", required=True, help="path to input dataset") args = vars(ap.parse_args()) # grab the list of images that we'll be describing print("[INFO] describing images...") imagePaths = list(paths.list_images(args["dataset"])) # initialize the data matrix and labels list data = [] labels = [] |
33行到36行解析命令列引數。我們這裡只需要一個簡單的開關，—dataset是kaggle 貓vs狗資料集的路徑。
然後我們將25000張圖片儲存的磁碟位置賦值給imagePaths，跟著初始化一個data矩陣，儲存提取後的特徵向量和類別labels。
說到提取特徵，我們接著這樣做：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# loop over the input images for (i, imagePath) in enumerate(imagePaths): # load the image and extract the class label (assuming that our # path as the format: /path/to/dataset/{class}.{image_num}.jpg image = cv2.imread(imagePath) label = imagePath.split(os.path.sep)[-1].split(".")[0] # extract a color histogram from the image, then update the # data matrix and labels list hist = extract_color_histogram(image) data.append(hist) labels.append(label) # show an update every 1,000 images if i > 0 and i % 1000 == 0: print("[INFO] processed {}/{}".format(i, len(imagePaths))) |
在47行，我們開始對輸入的imagePaths進行遍歷，對於每個imagePath，我們從磁碟中載入image，提取類別label，然後通過計算顏色直方圖來量化圖片。然後我們更新data和labels各自的列表。
目前，我們的labels是一個字串列表，如“狗”或者“貓”。但是，很多scikit-learn中的機器學習演算法傾向於將labels編碼為整數，每個標籤有一個唯一的數字。
使用LabelEncoder類可以很方便的將類別標籤從字串轉變為整數：
|
1 2 3 |
# import the necessary packages from sklearn.preprocessing import LabelEncoder from sklearn.svm import LinearSVC |
呼叫了 .fit_transform方法後，現在我們的labels表示為整數列表。
程式碼的最後一部分將資料劃分為訓練和測試兩組、訓練線性SVM、評估模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# partition the data into training and testing splits, using 75% # of the data for training and the remaining 25% for testing print("[INFO] constructing training/testing split...") (trainData, testData, trainLabels, testLabels) = train_test_split( np.array(data), labels, test_size=0.25, random_state=42) # train the linear regression clasifier print("[INFO] training Linear SVM classifier...") model = LinearSVC() model.fit(trainData, trainLabels) # evaluate the classifier print("[INFO] evaluating classifier...") predictions = model.predict(testData) print(classification_report(testLabels, predictions, target_names=le.classes_)) |
70和71行構造了訓練集和測試集。我們將75%的資料用於訓練，剩下的25%用於測試。
我們將使用scikit-learn庫實現的LinearSVC（75和76行）來訓練線性SVM。
最後，80到82行評估我們的模型，顯示一個格式整齊的報告，來說明模型的執行情況。
需要注意的一點是，我故意沒有進行調參，只是為了讓這個例子簡單，容易理解。不過，既然提到了，我就把LinearSVC 分類器的調參作為練習留個讀者。可以參考我以前的k-NN分類器調參部落格。
評估線性分類器
為了測試我們的線性分類器，確保你已經下載了：
1. 本部落格中的原始碼，可以使用教程底部的“下載”部分。
有了程式碼和資料集之後，你可以執行如下命令：
|
1 |
$ python linear_classifier.py --dataset kaggle_dogs_vs_cats |
特徵提取過程大約要花費1-3分鐘不等，具體時間根據機器的速度。
之後，訓練並評估我們的線性SVM：
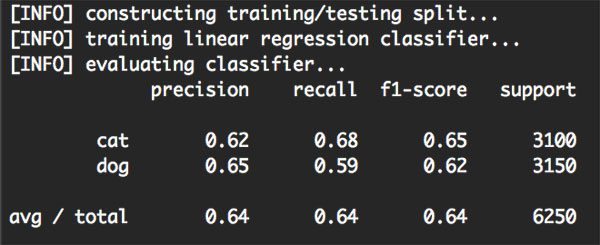
正如上圖所示，我們的分類精度有64%，大致接近本教程中調參後的knn演算法精度。
注意：對線性SVM調參可以得到更高的分類精度，為了使教程稍微短一點，而且不至於太複雜，我簡單地省略了這個步驟。
此外，我們不僅得到了和knn相同的分類精度，模型的測試時間也快的多，只需要將權重矩陣和資料集進行點乘（高度優化後），然後是一個簡單的加法。
我們也可以在訓練完成後丟棄訓練集，只保留權重矩陣W和偏置向量b，從而大大精簡了模型表示。
總結
在今天的部落格中，我討論了引數學習和線性分類的基礎概念。雖然線性分類器比較簡單， 但它被視為更多高階的機器學習和深度學習演算法的基石，並能很自然地擴充套件到神經網路和卷積神經網路中。
你看，卷積神經網路可以將原始畫素對映到類別標籤，類似於我們在本教程中所作的那些，只是評分函式f更復雜，並且引數更多。
引數學習的一大好處就是可以在訓練完畢之後，丟棄原訓練資料。我們可以只用從資料中學到的引數（比如，權重矩陣和偏置向量）來進行分類。
這使得分類變得非常高效，因為（1）我們不需要像knn那樣在模型中儲存一份訓練資料的拷貝（2）我們不用將測試圖片一個一個的和訓練圖片進行比較（一個O(N)的操作，並且當資料集很大時就變得非常麻煩）
簡而言之，這個方法明顯更快，只需一個簡單的點乘和加法。非常簡潔，不是嗎？
最後，我們在kaggle 狗vs貓的資料集上，利用Python, OpenCV, 和 scikit-learn進行線性分類。從資料集提取出顏色直方圖之後，我們在特徵向量上訓練一個線性支援向量機，並且得到64%的分類精度，這已經很不錯了，因為（1）顏色直方圖並非狗和貓特徵化的最佳選擇（2）我們沒有對線性SVM進行調參。
到這裡，我們開始理解了構建神經網路、卷積神經網路和深度學習模型的基本模組，但還有很長一段路要走。
首先，我們需要更詳細地瞭解損失函式，特別是如何使用損失函式來優化權重矩陣以獲得更準確的預測。 未來的部落格文章將更詳細地介紹這些概念。
打賞支援我翻譯更多好文章，謝謝！
打賞譯者
打賞支援我翻譯更多好文章，謝謝！
